基于改进的粒子群算法实现阶梯幅度量化相控阵天线的低副瓣
2010-10-16徐锋明孟令琴谢亚楠
徐锋明, 孟令琴, 谢亚楠
(上海大学特种光纤与光接入网省部共建重点实验室,上海 200072)
基于改进的粒子群算法实现阶梯幅度量化相控阵天线的低副瓣
徐锋明, 孟令琴, 谢亚楠
(上海大学特种光纤与光接入网省部共建重点实验室,上海 200072)
从统计意义上逼近传统的连续加权分布,利用无约束优化方法求出一组最优量化台阶.在此基础上,提出处理加权宽度的改进约束整数粒子群优化(particle swarm optimization,PSO)算法,实现阶梯幅度量化加权.设计了处理量化幅度权值的 Powell-PSO混合算法,进一步降低峰值副瓣电平.首次设计星载降水测量雷达 (precipitation radar,PR)相控阵天线的低副瓣,改进的 PSO算法在寻优能力、算法鲁棒性方面都得到了增强.
低副瓣;阶梯量化幅度;粒子群优化算法;星载降水测量雷达;相控阵天线
Abstract:This paper discusses the application of the particle swarm optimization(PSO)algorithm to accomplish low sidelobe for step-quantized amplitude phased array antennas.A group of multi-step quantized-amplitudeweights are obtained using an unconstrained optimization method,which approaches the traditional Taylor distribution statistically.An imp roved constrained PSO algorithm cop ing w ith step widths is used to achieve step-quantized amplitude.The Powell-PSO hybrid algorithm for quantizedamp litudeweights isp roposed to lower the peak sidelobe level for antennas.Low sidelobe for spaceborne p recipitation radar(PR)phased array antennas using the method is designed.The improved PSO algorithm has enhanced ability of optimization and better robustness.
Key words:low sidelobe;step-quantized amplitude;particle swarm optimization(PSO)algorithm;spaceborne p recip itation radar(PR);phased array antennas
星载降水测量雷达 (p recipitation rader,PR)要求天线具有低副瓣 (-30 dB)或超低副瓣 (-40 dB)的特性,因此,研制低副瓣或超低副瓣相控阵天线非常重要.
天线方向图综合是阵列天线设计的一个经典问题,研究方法可以分为传统方法 (包括 Chebyshev,Taylor[1]方法)和现代智能算法 (包括粒子群算法、遗传算法[2]).
为了降低制造成本、降低馈电网络的复杂度和提高系统的可靠性,在获得最低的峰值副瓣电平的同时,要求 T/R组件的种类越少越好.量化幅度加权[3-4]是其中的一种解决方法.Lee[3]首先采用梯度搜索算法对一个含有 400个单元的椭圆面阵进行了阶梯幅度量化研究,取得了 -36 dB峰值副瓣电平的效果.高铁等[4]研究了多阶振幅量化固态有源相控阵天线的口径设计方法,首先获得了理想的Taylor电流分布.为使量化后的波瓣功率与理想电流分布对应的波瓣功率之间的方差最小,采用非线性无约束优化方法求得方差最小值,同时求得一组最佳量化台阶.
Kennedy和 Eberhart[5]于 1995年提出粒子群优化 (particle swarm optimization,PSO)算法.虽然该算法的提出只有短短的十几年时间,但由于 PSO算法具有实现简单、所含参数少等特点,已经在各方面得到了广泛应用,其中在电磁工程和天线综合方面具有不错的表现[6].针对 PSO算法容易出现早熟收敛、陷入局部极值和后期收敛速度慢等缺点,研究者提出了大量的改进方法[7-9].
本研究首先基于统计学的方法求出一组量化台阶,为了实现阶梯幅度量化和进一步降低峰值副瓣电平,引入串联 PSO优化算法求解.该算法由处理离散、约束问题性质的约束整数 PSO算法和 Powell-PSO混合算法组成.使用该方法能够实现星载 PR天线的低副瓣,得出的 64阵元线阵结果比文献[10]给出的结果小 0.4 dB左右,证实了本研究方法的有效性.
1 量化台阶的求解
考虑一个以等间距 d排列、阵元总数为 N的线阵,此时,理想波瓣的阵因子可以表示为

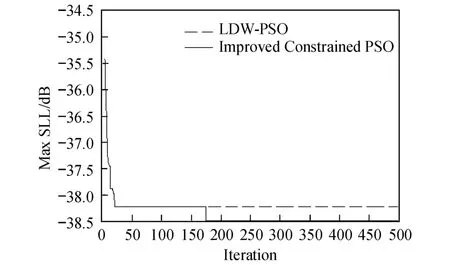
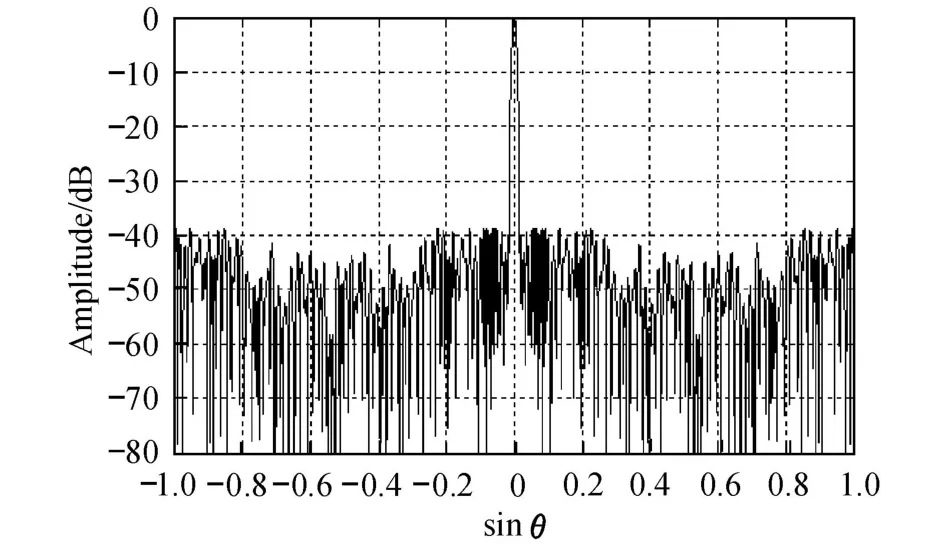
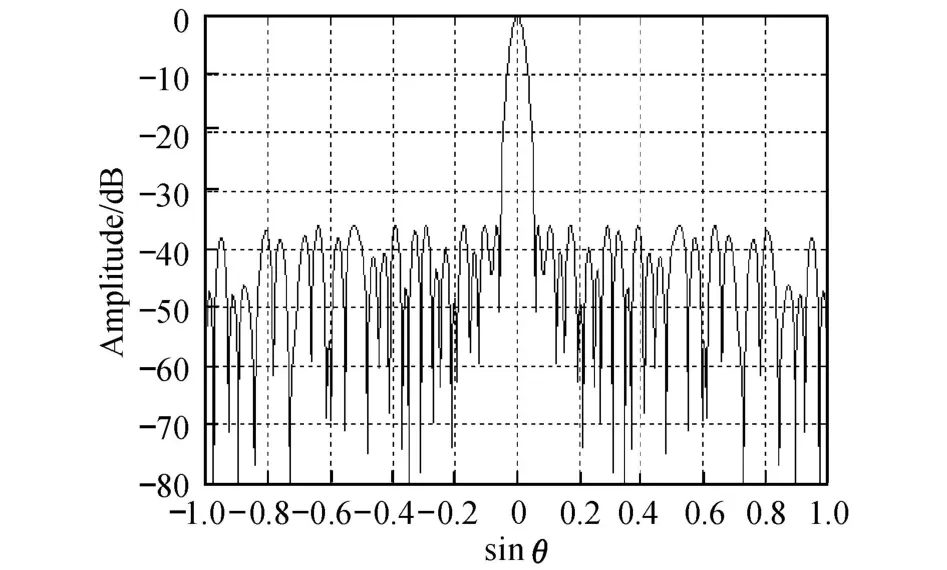
式中,In为第 n阵元的归一化理想电流幅度,λ为工作波长,θ为主波束方向与坐标轴 Z的夹角.用随机变量 Jn来代替式 (1)中的 In,Jn的量化取值为 C0,C1,…,CK(C0≡0,Ck-1 In可以是 Chebyshev或 Taylor分布.为便于讨论,将 [0,1]分成 K个子区间 [C0,C1],[C1,C2],…,[CK-1,CK].由计算机产生一组均匀分布在 [0,1]的伪随机数 Rn,当 In∈[Ck-1,Ck]时 ,令 式中,Pn为 In的取值概率. 由方差的定义,即 式中,〈Y〉表示对 Y求均值,Y*表示对 Y求共轭.可得 为了使经过量化幅度加权的功率波瓣 P(θ)最佳逼近连续加权产生的功率波瓣 P0(θ),必须使二者之间的方差σ2最小.为此,通过非线性无约束优化算法,求出方差σ2的最小值,同时也求得一组最佳量化台阶[C0,C1,…,Ck-1,Ck]. 最后,引入改进的 PSO算法,求出阵列天线阶梯幅度量化加权的最优加权宽度和最优量化幅度权值,实现天线的低副瓣. 采用阶梯量化幅度加权激励,此时线阵的阵因子式 (1)可以写为[10] 式中,In和Mn(n=0,1,…,N1-1)分别为量化幅度权值 (实数)和对应的加权宽度 (整数),N1为量化阶数.式 (6)可以采用 PSO算法来求解,相应的优化问题描述如下: 式(7)表示加权宽度要为正整数的约束关系,式 (8)表示各加权宽度的总和等于线阵阵元总数,式 (9)规定了归一化的幅度权值的大小,θi位于副瓣区.为了使算法更容易找到最优解,这里采用串联 PSO算法的策略,即取第 1节求出的量化台阶,通过改进的约束整数 PSO算法求出最优量化加权宽度Mn-Opt;取定Mn-Opt,通过 Powell-PSO混合算法求出最优量化幅度权值 In-Opt,进一步降低天线峰值副瓣电平. 2.1 PSO算法基本原理 PSO算法是一种基于群体的优化算法,可用于模拟鸟群或蜂群的飞行觅食行为,通过群体之间的竞争与协作而使群体达到最优.在 PSO算法中,每个粒子也就是解集 (D维)的一个解,都有一个飞行速度来调整粒子的飞行方向和移动距离,并且由适应度函数来评价每个粒子的好坏.粒子本身通过两个最优值来更新:一个是粒子本身找到的历史最优解,即个体最优值 Pb;另一个是群体找到的当前最优值,即群体最优值 gb.粒子的更新公式如下[12]: 2.2 约束整数 PSO算法 虽然大多数 PSO算法可用来求解连续空间优化问题,且已取得了巨大成功,但用于解决离散、约束优化问题的 PSO算法非常少.约束整数 PSO算法直接以各加权宽度构成的矢量作为粒子,即 xji=,其中 xji表示第 j次迭代的第 i个粒子.考虑约束条件式 (7)和 (8),算法在初始化时分别对粒子位置和速度作了如下处理. (1)粒子位置处理.函数 randint(1,N1,[M0imin,对每个粒子产生一个N1维矢量分别为加权宽度取值范围的最小值和最大值.接下来对粒子位置的每一维作变换,M0i(n) =其中 floor(Y)函数表示对 Y作向下取整.记 DM0i=,并对差值 DM0i从大到小排列,令Δ =N-对前Δ个对应的 TM0i(n)加 1即可. 基本的约束整数 PSO算法虽然能够处理离散和约束的问题,但容易收敛到局部最优解.为了提高算法找到全局最优解的能力,需在算法陷入局部极值后对粒子进行随机扰动,主要思想是:先由计算机随机产生一个正整数 Z∈[1,2,…,N1/2];在加权宽度索引矢量 [0,1,…,N1-1]中,随机选取 Z个元素,对选中索引元素对应的加权宽度进行 +Z2(整数)运算;同时在索引矢量剩余元素中,随机选取 Z个元素,对其所对应的加权宽度进行 -Z2运算,其中 Z2可取 1,2,3,…,这样能保证约束条件 (8). 算法主要步骤如下: Step 1 随机初始化粒子种群,包括粒子的位置、速度和惯性权重、学习因子等信息; Step 2 对位置、速度矢量分别进行取整操作,使其满足约束条件; Step 3 计算粒子的适应度值,将粒子的 Pb设置为当前位置,gb设置为初始群体中最佳粒子的位置; Step 4 对每个粒子的速度按式 (10)更新,并进行取整操作,粒子的位置按式 (11)进行更新; Step 5 将每个粒子的适应度值与其个体最优值的适应度值进行比较,若更好,则其个体最优值更新为当前粒子的位置; Step 6 将每个粒子的个体最优值的适应度值与群体最优值的适应度值进行比较,若更好,则群体全局最优值更新为当前的个体最优值; Step 7 判断算法是否满足收敛准则,如果满足 ,转向 Step 10,否则 ,执行 Step 8; Step 8 判断算法是否满足扰动操作条件,如果满足,执行 Step 9,否则,转向 Step 4; Step 9 对粒子进行随机扰动操作,转向 Step 7; Step 10 输出 gb,算法运行结束. 2.3 Powell-PSO混合算法 针对LDW-PSO算法容易出现早熟收敛、后期收敛速度慢、易陷入局部最优等缺点,提出在算法陷入停滞时,引入 Powell算法[13]进行局部搜索,提高了算法搜索到全局最优解的能力.该算法充分发挥了 PSO算法较强的全局搜索能力和 Powell算法较强的局部搜索能力,克服了各自的缺点,使得混合算法搜索到的解的质量、效率和算法的鲁棒性都优于单一的算法. 整个算法的思路如下:利用LDW-PSO算法进行全局搜索,当全局最优值在一定次数内未变化或变化很小时,对所有粒子进行适应度函数评价;对选取的适应度好的前 P(P=30% ×S)个粒子进行 Powell算法优化;经过优化后的粒子再进行 LDW-PSO算法优化,交替运行,直到满足终止条件. 整个算法的主要步骤如下: Step 1 随机初始化粒子种群,包括粒子的位置、速度和惯性权重、学习因子等信息; Step 2 计算粒子的适应度值,将粒子的 Pb设置为当前位置,gb设置为初始群体中最佳粒子的位置; Step 3 对每个粒子的速度按式 (10)更新,粒子的位置按式 (11)更新; Step 4 将每个粒子的适应度值与其个体最优值的适应度值进行比较,若更好,则其个体最优值更新为当前粒子的位置; Step 5 将每个粒子的个体最优值的适应度值与群体最优值的适应度值进行比较,若更好,则群体全局最优值更新为当前的个体最优值; Step 6 若算法出现全局最优值在一定迭代次数内未得到更新时,寻求适应度值较好的 P个粒子进行 Powell算法优化,而其他粒子的速度和位置按式 (10)和 (11)进行更新; Step 7 若满足算法终止条件,执行 Step 8,否则 ,转向 Step 3; Step 8 输出 gb,算法运行结束. 2.4 两种 PSO算法的串联 串联 PSO算法的主要步骤如下: Step 1 利用第 1节求得的量化台阶 [C0,C1,…,Ck-1,Ck],使量化幅度权值初值为,…,Ck-1,Ck]; Step 2 取定量化幅度权值 I0n,利用约束整数PSO算法求出最优的加权宽度 Step 3 取定加权宽度Mn-Opt,以 In为初值 ,利用Powell-PSO混合算法求出最优的量化权值分布 Step 4 若满足终止条件,则算法结束,否则,转向Step 2. 实例 1 两副星载 PR天线的参数如下:工作频率分别为 Ku波段和 Ka波段,阵元总数分别为 160和128单元,阵元间距分别为 15.0和 7.8 mm的线阵. (1)实现 Ku波段天线低副瓣的主要过程如下. Step 1 量化权值初值的确定. 线阵为 -40 dB Taylor分布连续加权,为简化计算量,采用激励电流对称加权的方式,本研究采用10阶量化幅度加权方式.通过非线性约束优化过程(Powell算法),求得最小方差σm2in=0.226 6,最优量化台阶 [0,0.117 1,0.202 6,0.296 5,0.400 7,0.500 0,0.603 3,0.714 2,0.818 1,0.920 5,1.000 0],量化权值初值 I0n=[0.117 1,0.202 6,0.296 5,0.400 7,0.500 0,0.603 3,0.714 2,0.818 1,0.920 5,1.000 0]. Step 2 最优加权宽度Mn-Opt的求解. 量化权值初值 I0n的取值与 Step 1相同,利用约束整数 PSO算法求得最优的量化加权宽度Mn-Opt=[13,10,5,6,7,5,6,8,8,12],相应的最低峰值副瓣电平PSLL为 -38.49 dB.改进的约束整数 PSO算法与约束整数LDW-PSO算法的收敛性能如图1所示. 图1 两种约束整数 PSO算法的收敛性能(Ku波段)Fig.1 Convergence ability of two constrained PSO(Ku band) Step 3 最优量化幅度权值 In-Opt的求解. 取定加权宽度Mn-Opt=[13,10,5,6,7,5,6,8,8,12],以量化权值 I0n为初值,利用 Powell-PSO混合算法求得最优量化权值 In-Opt=[0.063 2,0.203 8,0.298 0,0.390 2,0.496 2,0.590 2,0.695 3,0.828 0,0.925 8,1.000 0].相应的最低峰值副瓣电平 PSLL为 -39.02 dB.最终优化得到的线阵波瓣图如图2所示. (2)Ka波段天线的实现步骤与 Ku波段天线相同,其仿真计算的结果如下:最优加权宽度Mn-Opt=[12,5,6,4,5,4,5,7,8,8],最优量化幅度权值In-Opt=[0.114 3,0.204 6,0.305 9,0.398 8,0.500 8,0.603 5,0.707 8,0.816 3,0.921 0,1.000 0],最低峰值副瓣电平 PSLL为 -38.83 dB.约束整数 PSO算法的收敛性能如图3所示. 图2 优化后的 Ku波段天线波瓣图Fig.2 Antenna lobe pattern of the Ku band after optim ization 图3 两种约束整数 PSO算法的收敛性能(Ka波段)Fig.3 Convergence ability of two constra ined PSO(Ka band) 最终优化得到的线阵波瓣图如图4所示. 图4 优化后的 Ka波段天线波瓣图Fig.4 Antenna lobe pattern of the Ka band after op tim ization 实例 2 天线参数如下:线阵工作在 Ku波段,阵元间距为半波长,阵元总数为 64,采用对称激励加权方式,阶梯数为 8.实现天线低副瓣过程如下. Step 1 量化权值初值的确定. 量化权值初值 I0n=[0.127 8,0.244 4,0.351 6,0.471 4,0.596 4,0.718 6,0.862 2,1.000 0]. Step 2 最优加权宽度Mn-Opt的求解. 最优的量化加权宽度Mn-Opt=[6,4,3,2,3,3,4,7],相应的最低峰值副瓣电平 PSLL为 -34.83 dB.改进的约束整数 PSO算法与约束整数 LDW-PSO算法的收敛性能如图5所示. 图5 两种约束整数 PSO算法的收敛性能Fig.5 Convergence ab ility of two con stra ined PSO Step 3 最优量化幅度权值 In-Opt的求解. 最优量化权值 In-Opt=[0.139 0,0.260 8,0.388 0,0.520 1,0.624 4,0.755 4,0.881 2,0.999 8],相应的最低峰值副瓣电平 PSLL为 -35.95 dB.最终优化得到的线阵波瓣图如图6所示. 图6 优化后的线阵波瓣图Fig.6 Antenna lobe pattern after optim ization 表 1列出了两种算法独立运行 20次后,求出的线阵峰值副瓣电平的最小值、平均值、最大值和均方差.由表可见,Powell-PSO混合算法在解的质量、解的稳定性方面都优于单一的LDW-PSO算法. 表 1 两种算法比较Table 1 Compar ison of two algor ithm s 本研究采用串联 PSO算法实现了阶梯幅度量化星载 PR相控阵天线的低副瓣.针对算法易陷入局部极值的缺点,对处理加权宽度的约束整数 PSO算法加入扰动措施.Powell-PSO混合算法在算法鲁棒性、解的质量方面都优于单一的算法.仿真计算结果表明,该串联 PSO算法的寻优能力得到了较大提高.分析量化权值误差对天线的影响及如何用 PSO算法设计低副瓣量化加权的稀疏阵列天线将是下一步的研究工作. [1] V ILLENEUVE A T.Taylor patterns for discrete arrays[J]. IEEE Transactions on Antennas and Propagation,1984,32(10):1089-1093. [2] HAUPT R L.Thinned arrays using genetic algorithms[J]. IEEE Transactions on Antennas and Propagation,1994,42(7):993-999. [3] LEE J J.Sidelobes control of solid-state array antennas[J]. IEEE Transactions on Antennas and Propagation,1988,36(3):339-344. [4] 高铁,李建新.固态有源相控阵天线多阶振幅量化及副瓣特性的研究[J].电子学报,1994,22(3):11-17. [5] KENNDY J, EBERHART R C. Particle swarm optimization[C]∥Proceeding of IEEE International Conference on Neural Networks.1995:1942-1948. [6] ROB INSON J, RAHMAT-SAM II Y. Particle swarm op timization in electromagnetics[J].IEEE Transactions on Antennas and Propagation,2004,52(2):397-407. [7] 梁科,夏定纯.对粒子群优化算法的几种改进方法[J].武汉科技学院学报,2006,19(7):44-47. [8] 王俊伟,汪定伟.一种带有梯度加速的粒子群算法[J].控制与决策,2004,19(11):1298-1304. [9] 吴明,丁雷,曹卫华,等.一种克服粒子群早熟的混合优化算法[J].控制与决策,2008,23(5):511-519. [10] 张增辉,胡卫东,郁文贤.低副瓣相控阵天线量化幅度权值设计[J].电子学报,2007,35(3):580-584. [11] 林昌禄.天线工程手册 [M].北京:电子工业出版社,2002:436-438. [12] SHI Y H,EBERHART R.A modified particle swarm optimizer[C]∥ Proceeding of IEEE International Conference on Evolutionary Computation.1998:69-73. [13] POWELL M J D.An efficient method for finding the minimum of a function of several variables without calculating derivatives[J]. The Computer Journal,1964,7(2):155-162. (编辑:赵 宇 ) Realization of L ow Sidelobe for Step-Quan tized Am plitude Phased Array Antennas Based on M od if ied Par ticle Swarm Optim ization XU Feng-ming, MENGLing-qin, X IE Ya-nan TN 820 A 1007-2861(2010)04-0361-06 10.3969/j.issn.1007-2861.2010.04.006 2009-05-18 上海市科委国际合作项目(08590700500) 谢亚楠 (1962~),男,研究员,博士,研究方向为电磁场与微波技术.E-mail:yxie@shu.edu.cn

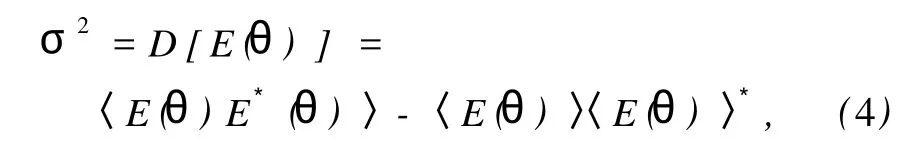

2 改进的 PSO算法
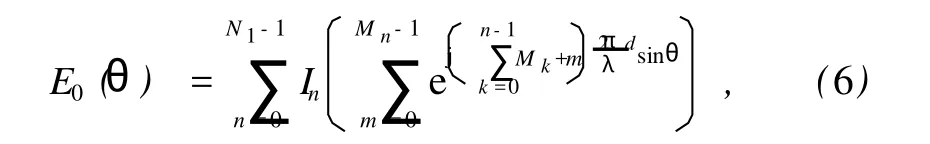
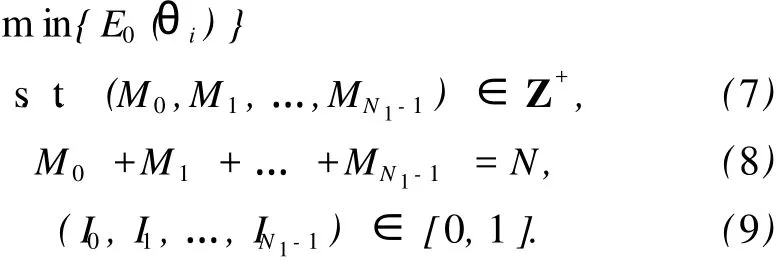


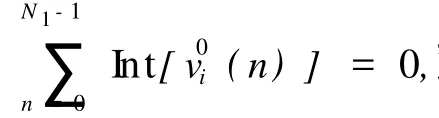
3 仿真计算




4 结 束 语
(Key Laboratory of Specialty Fiber Op tics and Op tical Access Networks,Shanghai University,Shanghai 200072,China)
