群体运动控制中的虚拟领导算法
2010-10-16刘维晓陈俊丽万旺根
刘维晓, 陈俊丽, 万旺根, 黄 炳
(上海大学通信与信息工程学院,上海 200072)
群体运动控制中的虚拟领导算法
刘维晓, 陈俊丽, 万旺根, 黄 炳
(上海大学通信与信息工程学院,上海 200072)
针对群体运动中的虚拟领导问题,提出一种多维空间中群体运动的虚拟领导算法.算法中的控制准则可以保证群中个体的状态变化始终与虚拟领导同步,碰撞检测和聚合规则可以有效控制群中相邻个体的距离,避免出现碰撞或离群现象.仿真结果表明,该算法可以很好地实现队列保持、聚合和避障的目的.
虚拟领导;碰撞检测;聚合
Abstract:For the problem of multi-agent systemswith a virtual leader,we introduce a flocking algorithm of multi-agents moving in the multi-dimensional space with a virtual leader.The control law s of the algorithm ensure synchronous changes of state of individuals w ith the virtual leader.Collision detection and aggregation rulescan effectively control the distance between neighboring individuals to avoid collision or moving too far from the group.Simulation gives good results in maintaining the queue,aggregation and obstacle avoidance.
Key words:virtual leader;collision detection;aggregation
群聚行为是自然界中一种非常普遍的现象.群聚行为中的生物个体虽然都很简单,但却能协同工作,表现出很复杂的行为,如集中觅食、共同防御和建造漂亮的巢穴等.这种群居性生物中产生出的集体行为被称为群体智能.群体智能存在于自然界的鸟群、鱼群、细菌群等各种群体行为之中[1].群体智能利用群体优势,在没有集中控制、不提供全局模型的前提下,为寻找复杂问题解决方案提供了新的思路.自 20世纪 80年代以来,群体智能已经成为人工智能以及经济、社会、生物等交叉学科的研究热点和前沿领域[2].最近几年,对群体智能中的控制理论研究正逐渐走进人们的视线,群体智能开始应用于一些控制领域,例如移动机器人的群体行为控制和机群的飞行控制等[3].
最早进行关于群体智能控制行为研究的是Reynolds[4],他于 1986年提出一个用于模拟鸟类聚集飞行行为的仿真模型,该模型中应用如下的定向行为规则:①分离规则;②列队规则;③聚合规则.模型提出后,在这三种行为规则的前提下出现了各种各样的改进模型和新的行为准则,例如用群体中两个相邻个体之间的局部吸引和排斥潜能定义分离和聚合行为准则[5],加入一些人工智能和回旋力来避障[6]等.Tanner等[7]提出了一系列可以控制群体稳定运动的控制准则,但是这些控制准则不能够规范个体的最终速度和整个群体的运动朝向.因为在某些情况下,规则对每个个体有特定的速度、朝向或是目的地的规范,但是对于整个群体而言没有一个共同的运动目标,因此,群体运动中的虚拟领导问题是一个重要的研究课题.
本课题研究的是多维空间中群体运动的虚拟领导问题.虚拟领导并不是一个实际存在的个体,而是人为设定的一个外部参考信号.虚拟领导的状态由控制准则提供,群中个体状态依据虚拟领导的状态变化而变化.2003年,Jadbabaie等[8]提出了一种控制群体运动的虚拟领导算法,算法中设定虚拟领导的状态是固定的,群中个体始终依照固定的速度和运动朝向进行运动,这种算法可以保证个体速度和运动朝向的一致性,但是不能满足对实际群体运动中动态变化状态的模拟.2006年,Olfati-Saber[9]提出了一种动态虚拟领导算法,算法中虚拟领导的状态依据群中相邻个体的速度和位置的动态累加获得,满足了一定的动态变化的模拟,但虚拟领导的控制中未加入碰撞检测,因此,算法不能满足大量群体长时间的运动模拟需要.
本研究提出了一种动态虚拟领导算法,算法中加入了一系列的控制准则,这些控制准则主要依赖于群体中个体邻近体的运动状态.控制准则中加入了避障和聚合规则,可以有效避免群中个体的碰撞和出现离群现象.控制准则应用于群体中的每个个体来控制个体的速度和位置状态.准则中引入了控制群体聚合度的参数 S和控制群体大小的参数ρ,可以很好地控制群体中个体之间的聚合程度和群体中个体的数目,防止过多自由个体的出现.具体实现流程图如图1所示.向.朝向是群中个体如何在局部空间被定义的一种指示,主要有 Roll,Pitch和 Yaw组成.Roll是指绕着空间的 z轴旋转 (朝着前后),Pitch是指绕着空间的 x轴旋转 (左右偏转),Yaw是指绕着空间的 y轴旋转(上下运动).Row,Pitch和 Yaw主要决定了群体中个体的运动朝向.本研究通过给每一个个体定义一个速度矢量 v(x,y,z)来调整个体在 x,y,z轴的运动方向.

图1 实现流程图Fig.1 Flow char t of the algor ithm

图2 定义的三维空间图Fig.2 Def in ition of the three-d im ensional graph
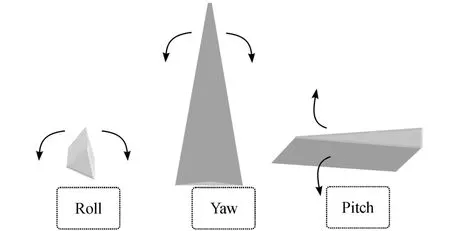
图3 空间中三个轴的旋转定义Fig.3 Def in ition of the three ax is rotation
1 实时运动模型构建
本研究假设群体中有 N+1个个体在三维空间中运动.三维空间中“前”对应着 z轴的正向,“左”对应着 x轴的正向,“上”对应着 y轴的正向,空间坐标如图2所示.
图3为空间运动的另一个重要因素 ——朝
每一个个体的实时运动模型定义如下:
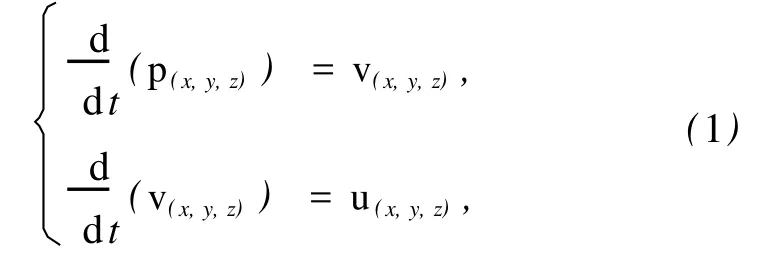
式中,p(x,y,z)∈R3N为群体中个体的位置矢量,v(x,y,z)∈R3N为群中个体的速度矢量,u(x,y,z)∈R3N为控制准则的反馈控制量.
在群体运动过程中,个体的速度和位置状态都是不断变化的,因此,需要虚拟领导的位置和速度状态也是不断变化的.控制准则应当保证群体中所有个体的状态变化与虚拟领导同步,因此,控制准则的设计应当满足以下两个设计原则:①群体中个体的状态变化应当保持一致性,并且以虚拟领导的状态为参考;②群体中相邻的个体之间应当保持一定的距离,并且要相互吸引,同时要避免碰撞[10].根据反馈控制输入的设计原则,设定控制输入的表达式如下:
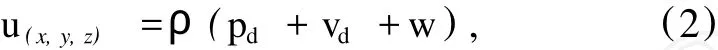
式中,pd,vd为个体为了达到虚拟领导的最优状态所需的位置和速度改变量,w为控制群体中个体的聚合程度函数,ρ为控制群体大小的输入量[3].

对于群体运动而言,必须使群中个体有一个相对稳定和一致的位置状态和速度状态,从而保持运动的一致性[11].因此,对于整个具有 N+1个个体的群体而言,个体 j为了达到虚拟领导的最优位置所需要的改变可用 pjd表示为

个体 j为了达到虚拟领导的最优速度所需要的改变可用vdj表示为
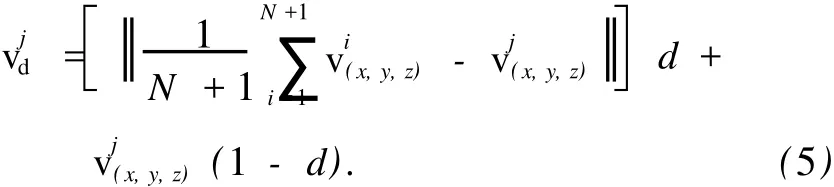
式 (4)和 (5)中的 d为一个可以控制群体聚合程度的值,取值范围在 0~1之间.d值越小,个体保持自身运动的趋势越大;d值越大,受其他个体运动的影响也就越大.
由式 (4)和 (5)可以确定整个群体中个体的位置和速度的状态改变量.根据控制准则的设计原则,除了要考虑位置和速度的状态改变外,还需要考虑群体运动中另一个重要问题——躲避障碍.算法中的避障并不是指躲避障碍物,而是为了保持相邻个体间的相对安全距离,避免碰撞和出现个体离群现象.
2 避障设计
避障设计是控制准则的另一个重要的组成部分,根据 Reynolds的算法设计原则,群体中相互临近的个体应当保持一定的距离.如果相邻个体之间的距离太近,它们应当自动分离;反之,当个体的距离太远,它们应当自动聚合[12].
假设群体中的最大可视距离是 smax,即当群体中的两个个体的距离小于 smax时,可认为它们是相邻的个体.当相邻个体的距离小于所设定的距离 d(d 根据上述群体运动的行为准则,可知避障设计是一个复杂的模糊行为.对于群体中的相邻个体 i,j,设定两个模糊控制函数[13]f(Δpdi,j)和 h(Δpdi,j),其中Δpdi,j如式 (3)所示.当相邻个体 i,j的距离小于设定的距离 d(d 图4 模糊控制函数Fig.4 Fuzzy control function 根据设定的模糊控制函数,可得如下的分离、聚合控制表达式: 在群体的运动过程中,个体之间的距离是随时间不断变化的,因此,群中个体的邻近个体也不是固定的.聚合控制准则应当把个体的所有邻近个体的状态包括在内,因此,聚合控制准则也是一个随时间不断变化的量.将分离聚合控制函数应用到个体 i的所有邻近个体,得到分离聚合准则 w为 在群体运动过程中,若群体数目过于庞大则容易造成个体的离群现象发生,影响群体运动的仿真效果,因此,应当添加一个控制群体大小的参数.设控制群体大小的参数为ρ,其大小主要取决于个体 j的当前位置与中心位置之间的距离,用下式表示: 反馈控制设计完毕后,还需对个体在运动中的运动朝向作如下定义: 式中,rx,ry,rz分别为旋转角度在 Pitch,Yaw,Rdl三个方向上的分量值,vx,vy,vz为速度矢量 v(x,y,z)在三维空间 x轴,y轴,z轴方向的数值,g为重力,l可用个体的速度矢量表示如下: 式中,vn为个体的当前速度,v0为个体前一时刻的速度. 综上可知,群体中的控制准则是为了规范群体中个体的运动状态、规范个体在运动中每一个时刻的状态改变量.个体的位置、速度和旋转角度的实时变化都要以虚拟领导为参考,同时群中相邻个体间应当保持一定的安全距离,尽量避免离群现象的发生. 本研究将群体运动中的控制准则用 OpenGL在VC++6.0上进行仿真.OpenGL是专业的图形程序接口,是一个功能强大、调用方便的底层图形库,可使本研究设计的群体运动控制规则有一个方便直观的显示.在仿真过程中,可以自由调节群的数目和每个群体中个体的数目,不同的群体用不同的深浅进行区别显示. 本研究在仿真中给群体运动的范围设定了一个边界(30,30,30),超过边界范围的个体成为自由活动的个体.个体的初始位置和速度矢量设定一个相同的随机值,并受设定边界的制约.试验中通过rand()函数为速度矢量和位置矢量取值,具体值为(rand()* 30/5,rand()* 30/5,rand()* 30/5).设定个体的实时运动速度大小由个体的速度矢量所决定,具体大小由下式实现: 根据试验效果,设定聚合控制参数 S的取值为0.55,使个体偏重于其他邻近个体的影响.仿真测试平台配置如表 1所示.具体的仿真结果如图5~图8所示. 表 1 测试平台Table 1 Test platform 图5 未加入控制准则的群体运动Fig.5 M ulti-agentsmovement w ithout control laws 图5所示为未加入控制准则的群体运动.由图可知,群体运动比较杂乱,整个群体的运动没有统一的运动朝向,运动过程中容易产生离群现象,随着时间的推移,个体都已独自运动,无法成群.图6为未加入避障规则的群体运动,个体之间不能很好地保持一定的距离,容易产生碰撞现象.图7和图8为加入了控制原则的群体,从仿真结果看,整个群体中的个体都是朝着相同的方向运动,并且保持了一定的距离,没有出现碰撞现象. 本研究所提出的动态虚拟领导算法与文献[8-9]中提出的虚拟领导算法相比,虽然在算法的复杂度上有所增加(具体表现在群体从初始杂乱状态达到稳定状态的时间),但是从整个群体的运动模拟显示中可以看出,本算法可以很好地控制群体中个体的运动状态,达到了群体模拟的预期效果.三种算法的具体比较如表 2所示,其中第二个比较项为本算法选用 25个个体在程序运行 10 s时进行统计的结果. 图6 未加入避障规则的群体运动Fig.6 M ulti-agentsmovement w ithout collision detection and aggregation rules 图7 算法控制下的多群体运动Fig.7 M ulti-agentsmovement w ith vir tual leader algor ithm 图8 算法控制下的三个群体运动Fig.8 Three agen ts m ovem en t w ith v ir tual leader algor ithm 表 2 算法比较Table 2 Algor ithm compar ison 本研究提出的虚拟领导算法可以有效地保证群中个体运动状态变化的一致性,降低了群体运动过程中离群现象产生的概率,减少碰撞现象的发生,实现群体运动中的队列、队形保持.然而,以下方面有待改进:①进一步优化虚拟领导算法,缩短个体达到稳态的运行时间;②尽可能地扩大可视范围,减少自由个体的影响,同时平衡算法的复杂度和稳定性;③解决不同群之间的碰撞检测问题. [1] KENNEDY J,EBERHART R C.Swarm intelligence[M].USA:Academic Press,2001:10-12. [2] OLFATI-SABER R,MURRAY R M.Consensus problems in networks of agents with switching topology and timedelays[J]. IEEE Transactions on Automatic Control,2004,49(9):1520-1533. [3] SHIH,WANG L,CHU T G,et al.Flocking of multiagent systemswith a virtual leader[C]∥Proceeding of the 2007 IEEE Symposium on Artifical Life.2007:287-294. [4] REYNOLDS C W. Flocks, herds, and schools: a distributed behavioral model[C]∥Computer Graphics,SIGGRAPH’87 Conference Proceedings.1987:25-34. [5] GAZI V,PASSINO K M.Stability analysis of swarms[J].IEEE Transactionson Automatic Control,2003,48(4):692-697. [6] TANNER H G. Flocking with obstacle avoidance in switching networks of interconnected vehicles[C]∥IEEE International Conference Robotics and Automation.2004:3006-3011. [7] TANNER H G,JADBABA IE A,PAPPAS G J.Stable flocking of mobile agents[C]∥Proceeding of the 42ndIEEE Conference on Decision and Control.2003:2010-2021. [8] JADBABA IE A,L IN J,MORSE A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control,2003,48(6):998-1001. [9] OLFATI-SABER R. Flocking for multi-agent dynamic systems:algorithms and theory[J].IEEE Transactions on Automatic Control,2006,51(3):401-420. [10] PESRAM I R,GORDON B W.Control and cohesion of energetic swarms[C]∥American Control Conference.2008:129-134. [11] WANG Z Y,GU D B.Distributed cohesion control for leader-follower flocking [C]∥ Fuzzy Systems Conference.2007:1-6. [12] WANG Z Y,GU D B.Fuzzy control of distributed flocking system[C]∥IEEE International Conference on Mechatronics and Automation.2007:2807-2812. [13] SHIH,WANGL,CHU T G,et al.Tracking control for groups of mobile agents[C]∥American Control Conference.2007:3265-3270. (编辑:赵 宇 ) Vir tual L eader Algor ithm for Flock ing M otion Control L IU Wei-xiao, CHEN Jun-li, WAN Wang-gen, HUANGBing TP 391.9 A 1007-2861(2010)04-0349-06 10.3969/j.issn.1007-2861.2010.04.004 2009-01-09 国家高技术研究发展计划(863计划)资助项目 (2007AA01Z319);上海市教委重点学科建设资助项目 (J50104);国家自然科学基金资助项目(60873130) 陈俊丽 (1972~),女,副教授,博士,研究方向为多媒体信息处理.E-mail:jlchen@staff.shu.edu.cn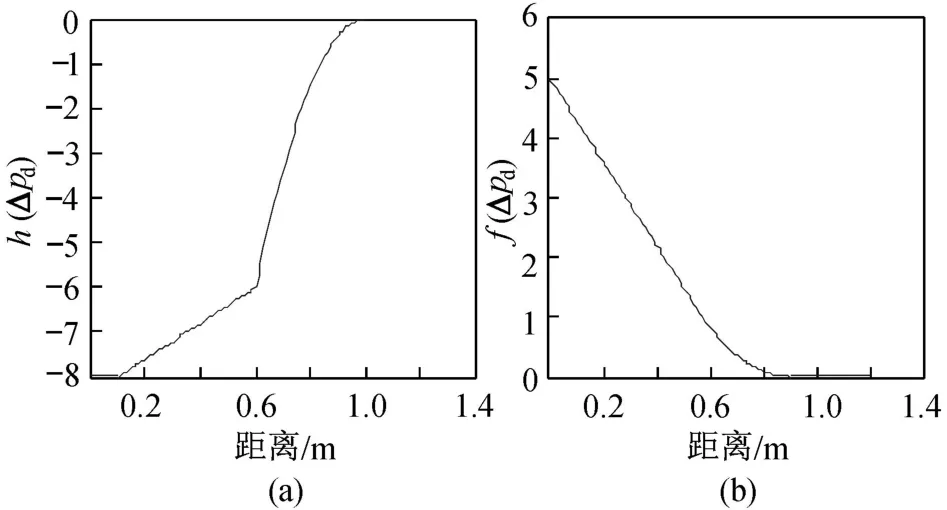
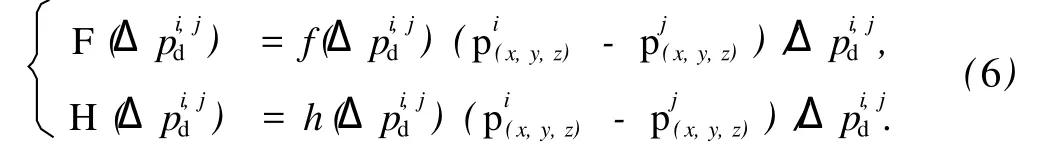

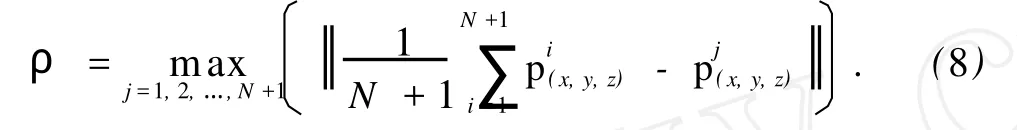
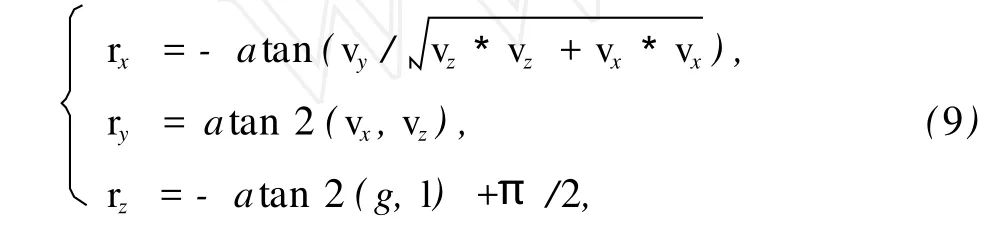
3 仿真结果分析






4 结 束 语
(School of Communication and Information Engineering,Shanghai University,Shanghai 200072,China)
