John基等价条件的推广

郑 敏, 冷岗松

(上海大学 理学院,上海 200444)

John基等价条件的推广

郑 敏, 冷岗松

(上海大学 理学院,上海 200444)

John基在凸体几何分析中占有重要地位,是研究凸体包含最大体积椭球的基础.将 John基的 3个等价条件推广到双 John基,并给出证明.

John基;接触对;极体;双 John基

Abstract:John bases occupy an important place in convex geometry,and are fundamental in studying maximal ellip soid contained in convex.In thispaper,we extend John bases to generalized John bases and p resent the proof.

Key words:John bases;contact pair;polar;double John bases

1 John基及其等价条件

定义 1[8]K表示包含原点的凸体,则 K＊表示K的极体,满足下面条件:K＊={x|〈x,y〉≤1,对于任意的 y∈K}.

定义 2[3]C1是 Rn紧凸集,C2是 Rn中线性形式的紧子集,设 C1⊂C＊2,(x,y)称为 (C1,C2)的接触对,如果满足以下条件:

定义 3[8]集合 T的凸包是 T中所有点的凸组合所组成的集合.

BALL[5]提出的 John定理如下:

定理 1 每一个凸体 K都包含着唯一一个体积最大的椭球Bn2,当且仅当 B2n⊂K,且在 K的边界上存在m个单位向量 u1,u2,…,um和m个正数 c1,c2,…,cm(其中 m是某个正整数)满足

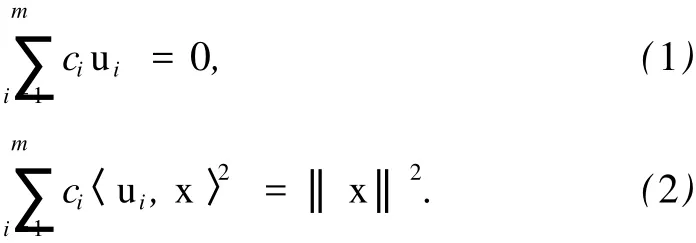
若且对于任意的x都成立,则称{ui}为 John基.

定理 2 设 Rn为 n维空间,ui为 Rn中单位列向量,ci是正实数,i=1,2,…,m,In为 n阶单位矩阵,则下面 3个等式等价:

John定理给出了包含在凸体内的体积最大的椭球为欧氏球的充要条件,Gordon等[6]将 John定理推广到更为普遍的情况.

定理 3 设 C1和 C2为 Rn中的两个紧凸集,并且 C1的凸包有非空内点,o∈conv(C2).如果conv(C1)位于 C＊2中,并且体积最大,则存在 (C1,C2)的 m0,使得

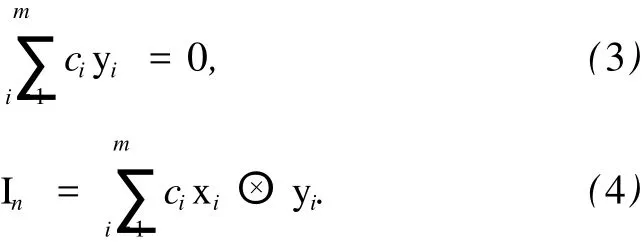
定理 4 设 C1和 C2为 Rn中的两个紧凸集,并且 C1的凸包有非空内点,o∈conv(C2),(xi,yi)1≤i≤m是 (C1,C2)的 m 个接触对 ,则下面 3个等式等价:

2 John基推广形式的等价证明

本节给出推广 John基的等价形式,在证明之前先给出一些引理.

引理 1 A为 n×n的矩阵,x为 Rn中的列向量,若 Ax=0对于任意的 x都成立,则 A=0.

引理 2 A为 n×n的对称矩阵,x为 Rn中的列向量,〈Ax,x〉=0对于任意的 x都成立,则 A=0.

引理 3 α,β,γ表示 Rn中的列向量,则 (α⊗β)γ=〈β,γ〉α.

证明 设 α′=(α1,α2,…,αn),β′=(β1,β2,…,βn),γ′=(γ1,γ2,…,γn)为 Rn中的列向量 ,则

所以 ,(α⊗β)γ=〈β,γ〉α.

定理 4的证明 先由 (2)推导 (3).

由引理 3,可得

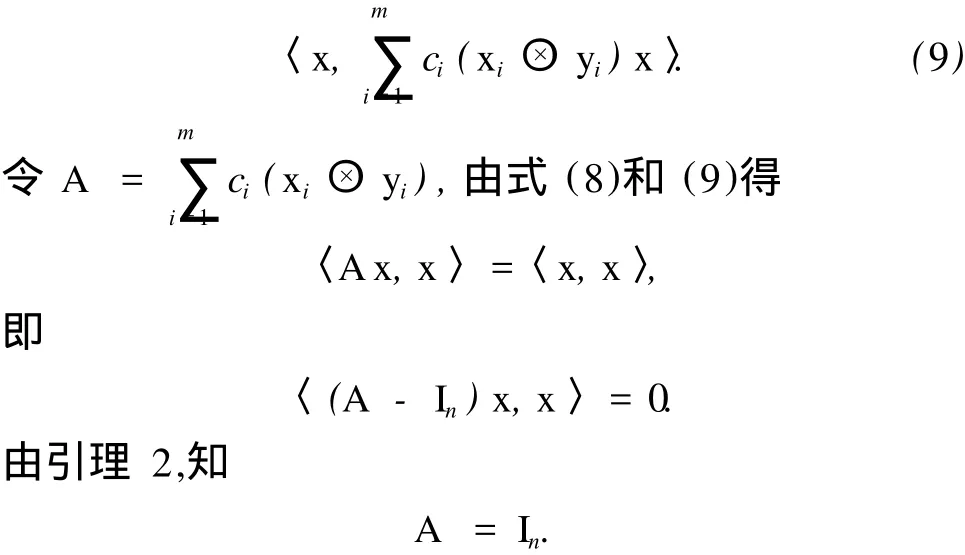
[1] BALL K.Ellipsoids of maximal volume in convex bodies[J].Geometry Dedicata,1992,41(2):241-250.

[2] BALL K.Volumes of sections of cubes and related problems[M]∥ Geometric Aspects of Functional Analysis.Berlin:Springer-Verlag,1989:251-260.

[3] GIANNOPOLOS A,PERISSINAKI I, TSOLOM ITIS A.John’s theorem for an arbitrary pair of convex bodies[J].Geometry Dedicate,2004,84:63-79.

[4] LUTAW E,YANG D,ZHANG G.A new ellip soid associated with convex bodies[J].Duke Mathematical Journal,2000,104(3):248-250.

[5] BALL K.An elementary introduction to modern convex geometry[M]∥ Flavors of Geometry. Cambridge:Cambridge University Press,1997:1-13.

[6] GORDON Y,L IVAK A E,MEYER M,et al.John’s decomposition in the general case and applications[J].Journal Differential Geometry,2004,68(1):99-119.

[7] GRUBER PM,SCHUSTER F E.An arithmetic p roof of John’s ellipsoid theorem[J].Archivder Mathematike,2005,85(1):82-88.

[8] GARDNER R J.Geometric tomography[M].2nd ed.Cambridge:Cambridge University Press,2006:9-10,188.

(编辑:孟庆勋)

Generalization for Equivalence of John Bases

ZHENGM in, LENG Gang-song
(College of Sciences,ShanghaiUniversity,Shanghai200444,China)

O 186.5

A

1007-2861(2010)04-0380-03

10.3969/j.issn.1007-2861.2010.04.010

2009-05-25

冷岗松 (1961～),男,教授,博士生导师,博士,研究方向为凸几何、几何分析.E-mail:gleng@staff.shu.edu.cn