图的逆符号边全控制的性质

黄中升

（廊坊师范学院 数信学院，河北 廊坊 065000）

图的逆符号边全控制的性质

黄中升

（廊坊师范学院 数信学院，河北 廊坊 065000）

本文将图的符号边全控制引申为图的逆符号边全控制，并在此基础上研究图的逆符号边全控制数的性质.

图；逆符号边全控制函数；逆符号边全控制数

1 引言

本文所指的图均为无向简单图，文中未说明的符号和术语同于文献[1].

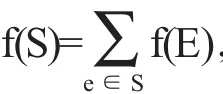
近年来，图的控制概念得到延伸和推广[2-3]，2006年徐宝根教授定义了符号边全控制[4].本文将图的符号边全控制引申为图的逆符号边全控制，并在此基础上研究图的逆符号边全控制数的性质.

定义1[4]设G=(V,E)为一个非空图，一个函数f:E→{-1,1}，如果对每一条边 e∈E，均有 f(N(e))≥1成立，则称f为图G的一个符号边全控制函数，图G的符号边全控制数γ'st(G)=min{f(E)|f为图G的符号边控制函数}.

下面引入图的逆符号边全控制的概念.

定义2 设G=(V,E)为一个非空图，对于图G的一个函数f:E→{-1,1}，如果对任意e∈E(G)，均有f(N(e))≤1成立，则称f为图G的一个逆符号边全控制函数，图G的逆符号边全控制数为γ'st(G)=max{f(E)|f为图G的逆符号边全控制函数}.对于图G的一个逆符号边全控制函数f，如果不存在图G的逆符号边全控制函数g(f≠g)，使得对于任意的e∈E，均有g(e)≥f(e)，则称f是G的一个极大逆符号边全控制函数.如果图G的一个逆符号边全控制函数f的权重 f(E)=γ'st(G)，则称 f是图 G 的一个 γ'st(G)函数.特别地，补充定义 γ'st(K1)=γ'st(K2)=0.

利用定义2能够解决图论中关于边集的一个划分问题：如果将一个给定图G的边集E划分为E1和E2两类，使得G的每条边的边邻域中第一类边至多比第二类边多一条，那么两类边的数目之差|E1|-|E2|的最大值就是这个图的逆符号边全控制数.

2 主要结果

定理1 对任意非空简单图G，均有γ'st(G)≡|E(G)|(mod2)

证明 设f是图G的一个γ'st函数，令P={e∈E|f(e)=1}，M={e∈E|f(e)=-1}，则 |E(G)|=|P|+|M|.

当|E(G)|为奇数时，令|E(G)|=2k+1,则|P|+|M|=2k+1，γ'st(G)=|P|-|M|=|P|-(2k+1-|P|)=2|P|-2k-1为奇数；当|E(G)|为偶数时,令|E(G)|=2k,则|P|+|M|=2k,γ'st(G)+|P|-|M|=|P|-(2k-|P|)=2(|P|-k)为偶数.从而有 γ'st(G)≡|E(G)|(mod2)．

定理2 对任意两个不交的图G1和G2，均有

由定义显然可得.

定理3 设f为图G的一个逆符号边全控制函数，则f为图G的一个极大的逆符号边全控制函数当且仅当对于满足f(e)=-1的任意一条边e∈E，都存在边e0∈N(e),使得f(N(e0))∈{0,1}.

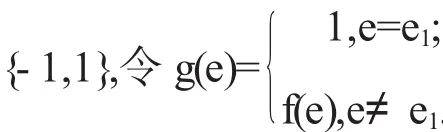
充分性 若f不是极大的逆符号边全控制函数，则存在一个极大的逆符号边全控制函数g，使得g>f,即对任意e∈E，有g(e)≥f(e)，且至少存在一条边 e'∈E，有 g(e')>f(e')成立.因而有 f(e')=-1，g(e')=1.由假设可知存在一条边e0∈N(e'),使得f(N(e0))∈{0,1}，但由于对任意 e∈N(e'))，有 g(e)≥f(e)，且 g(e')=f(e')+2，我们有 g(N(e0))=f(N(e0))+2≥2，与 g为逆符号边全控制函数相矛盾.证毕.

定理4 对于任意非空图G,均有γ'st(G)+γ'st(G)≥2,并且此下界是最好可能的.

证明 设f为G的一个权重最小的符号边全控制函数,则γ'st(G)=f(E).令g=-f,则对于任意e∈E,有g(N(e))=-f(N(e))≤-1,由定义2和定理3可知,g是G的一个逆符号边全控制函数,但不是G的一个极大逆符号.从而 γ'st(G)>g(E)=-f(E)=-γ'st(G),故 γ'st(G)+γ'st(G)>0.由于 γ'st(G)和 γ'st(G)具有相同的奇偶性,因此 γ'st(G)+γ'st(G)≥2.

对于2n阶星图K1,2n-1,由定义1和定义2易知,γ'st(K1,2n-1)=-1，γ'st(K1,2n-1)=3,从而 γ'st(K1,2n-1)+γ'st(K1,2n-1)=2,因此定理给出的下界是最好可能的.证毕.

这样，定理4给出了图G的逆符号边全控制数和符号边全控制数的关系.

〔1〕Bondy J A,Murty V S R.Graph Theory with Applications[M],Elsevier,Amsterdam,1976.

〔2〕Haynes T W,Hedetniemi S T,Slater P J,Fundamentals ofDominationinGraphs[M].New York,1998.

〔3〕Haynes T W,Hedetniemi S T,Slater P J,Domination in Graphs[M].New York,1998.

〔4〕徐宝根.关于图的符号边全控制[J].华东交通大学学报,2006,23(2):129-131.

O157.5

A

1673-260X（2010）06-0010-02

河北省教育厅2009年自然科学研究计划（2009331）;河北省自然科学基金(A2008000128);廊坊师范学院青年项目（LSZQ200225）; 廊坊师范学院科学研究项目（LSZY200901）