浅谈《线性代数》教学改革与实践

邵红梅

（廊坊武警学院 基础部，河北 廊坊 065000）

浅谈《线性代数》教学改革与实践

邵红梅

（廊坊武警学院 基础部，河北 廊坊 065000）

结合《线性代数》课程本身的特点和学生的实际情况,通过对线性代数课程的教学实践,从三个方面阐述了如何提高线性代数的教学效果.

线性代数；形象化；具体化；联系；思维能力

线性代数课程在高等工科学校的教学计划中是一门基础理论课，也是研究生入学考试的一门必考课程.这门课程是中学代数的继续和提高，它的思想和方法如今已经渗透到数学的各个领域中.而且随着计算机的快速发展，用代数方法解决实际问题已渗透到现代科学、技术、经济、管理的各个领域，尤其在计算机、通讯、电子等学科领域其重要性和实用性日渐显现.但线性代数课程也同时存在着概念多、定理多，内容抽象的特点，使得学生在学习时普遍感到抽象、枯燥，缺乏主动学习的积极性，也造成了学生数学应用意识的淡薄.如何上好线性代数课，如何提高线性代数的课堂教学效果，一直受到人们的关注.下面结合自己的教学，通过多年的教学实践，对这门课程的教学进行了改革，收到了很好的效果.主要作了以下几方面的努力和尝试：

1 将抽象的概念具体化、形象化

线性代数一般继一年的微积分课程后开设，此时学生已初步具备高等数学的思维能力.但线性代数的概念一般都比较抽象，大多学生会感到无从入手，适当将抽象的概念具体化，形象化，从他们熟悉的知识或例子入手，可以提高学生的学习兴趣，加深其对基本概念的理解.例如在学习n阶行列式的概念时，对于n阶行列式的含义，学生会感到很抽象，产生畏难情绪.针对这种情况，以学生在中学数学中学过的解二元线性方程组为例引出二阶行列式的定义，则使学生感到轻松易学.然后提出三阶行列式如何定义的问题，让学生参与该定义的过程，学生很快会给出三阶行列式的定义，在这种氛围下，再逐步引出四阶、五阶直至n阶行列式的定义，这样学生就较容易掌握n阶行列式的概念;再例如，在讲解矩阵的运算时，可以利用常用的数的四则运算来推导矩阵的四则运算，矩阵的加法减法运算可以举例为特定人群的工资表作为一个矩阵的同时加薪和减薪问题，然后介绍矩阵的乘法，学生很自然会思考一个数表和另一个数表相乘会遵循什么规则，在给出乘法规则后，学生感觉很难理解，甚至提出为什么不能像矩阵与矩阵的加法那样规定，然后教师举出一例来说明矩阵乘法的用途.例如，设有n个未知数m个方程式的线性方程组:

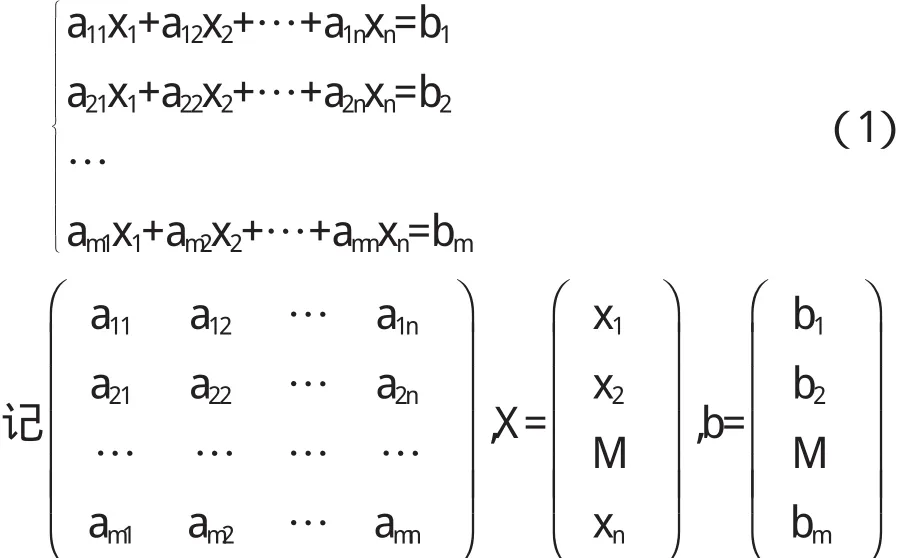
学生们不难自己求出A X，它正好就是b，即A X=b(2).这学生既看到了矩阵乘积的应用，又加深了对该法则的理解，更重要的是它可以使我们可以想象是否可以用矩阵的某些运算来处理线性方程组.通过类似问题的提出，增强了学生探索问题的兴趣，培养了创新意识和素质.

2 串联内容，注意联系

线性代数各章节的内容，不是孤立割裂的，而是相互渗透、紧密联系的，所以教师在授课过程中应注意各章节内容之间的联系，尤其是对各个概念的等价条件，一定要引导学生去总结发现，这样既使学生不会产生概念混淆，条理混乱，又锻炼了学生的逻辑思维能力.如A是n阶方阵，若:|A|≠0(称A为非奇异阵)则以下命题等价：

（1）存在若干个初等阵P1，P2，…，Pn，使得PnPn-1…P1A+E；

（2）A可以经过有限次初等行变换化为单位矩阵；

（3）A是可逆阵；

（4）存在n阶方阵B，使得A B=B A=E；

（5）r(A)=n(称A是满秩)；

（6）A可表示为若干个可逆阵的乘积；

（7）A可表示成若干个初等阵的积；

（8）A的列向量组线性无关(列满秩)；

（9）A的行向量组线性无关(行满秩).

再例如，线性代数的核心问题就是“线性方程组”问题，由此引出矩阵和向量的概念.历年来，学生对“向量组线性相关性”的问题都不能透彻地理解.如果将矩阵和向量组密切地联系起来，则线性方程组既可以看作矩阵方程，又可以看作向量组的线性相关性问题.看清了它们之间的联系对于线性方程组的问题就不仅仅可以从矩阵的初等变换着手，还可以从向量的相关性作为切入点，这样就为学生解决问题提供了方法，拓宽了思路.

3 注重学生思维能力的培养

教与学的过程中，我们除传授数学知识外，更应注重培养学生发现问题的能力和数学思维能力，即所谓“授之与鱼不如授之与渔”.在教学内容中渗透数学思想方法，对学生思维能力的培养是十分重要的.比如：在讨论完矩阵的乘法之后，我们可以讨论这样一个问题：矩阵可不可以有类似于数的除法，如果可以怎样来做？如果不可以为什么？这个问题提出以后，同学们众说纷纭，因为数的除法实质就是被除数乘以除数的倒数，那么矩阵有所谓的“倒数”吗？又因为矩阵的乘法不满足交换律，矩阵这个所谓的“倒数”唯一吗？有了这些想法，我们很自然的就引出了逆矩阵的概念，并且知道逆矩阵是唯一的.

另外，贯穿《线性代数》的突出思想方法之一就是“初等变换”的思想方法.利用初等变换理论作为基础可建立矩阵的秩、逆，向量组与向量空间，线性方程组，矩阵的对角化，线性变换等理论，进而再考虑抽象空间到抽象空间上的线性变换.能够掌握贯穿学科的若干思想方法其实就是找到了攀登整个学科高峰的捷径，学会思想方法对学习线性代数是大有裨益的，而且对自学能力的培养会起到促进作用.

以上是在线性代数教学过程中的一些想法和实践，希望能对教授此门学科的教师起到借鉴作用，也希望对学习线性代数的同学有所帮助.

〔1〕同济大学数学教研室.线性代数:第2版[M].北京:高等教育出版社,1997.

〔2〕赵琼.关于线性代数教学改革和教学实践的思考.科教文汇，2007（8）（上旬刊）.

〔3〕吴天毅.线性代数教学内容改革的研究与实践.天津轻工业学院学报数学专刊，2003（12）.

G642.4

A

1673-260X（2010）08-0207-02