仓库容量有限允许缺货条件下的随机存储模型

霍丽娜

（榆林学院 数学系，陕西 榆林 719000）

仓库容量有限允许缺货条件下的随机存储模型

霍丽娜

（榆林学院 数学系，陕西 榆林 719000）

对允许缺货的随机存储问题，建立了仓库容量有限并可以租赁仓库的存储模型，给出了模型的一般算法，较好地解决了多种商品在允许缺货条件下的最佳订货点的确定问题.

随机存贮；存储销售周期；惩罚函数法

1 问题的提出

企业生产需定期购进各种原料，商家销售要成批地购进各种商品.无论是原料或商品，都存在如何存贮的问题.库存冗余则存贮费用较高，库存短缺则无法满足需求，影响利润，所以许多商家为了满足市场的随机大量需求，采用租借别人仓库的方法，但是一般租借别人仓库都比使用自己仓库的费用高.因此，在这种情况下的实际的生产过程中，采用有效的库存管理方法将起到调节供需余缺、保证生产正常进行的作用，从而有力的降低不利损耗，提高企业效益.显然，在市场经济蓬勃发展的今天，研究这样一个可以服务广大工商界的问题的重要性不容忽视.

2 符号说明

T 商品存贮销售周期

ki第i种商品的库存下降速率（销售速率）

E(X)供货时间的数学期望

s某种商品在一个周期T中的总损失费用

S m种商品在一个周期内的总损失费用

Z 商品在一段时期内的总损失费用

t0某一周期T的开始时刻

t1库存商品量L售完时刻

t2所订商品到位时刻

t3租借仓库中商品售完时刻

t4自己仓库中商品库存量降至L的时刻

Q0i第i种商品在自己仓库中的库存体积容量

Qi第i种商品被补充到的固定体积容量

3 模型基本假设

（1）存贮时先将商品存入自己的仓库，剩余的存入租借的仓库.

（2）出售时先出售租借仓库中的商品，待其被销售完，再销售存在自己仓库中的商品.（3）假设仓库开始库存第i种商品数量为Li.（4）当商品库存下降速率一定时，任一阶段中商品的库存量可取其中间值.

（5）商品供货时间X虽然是随机的，但因其上下波动不大，故可采用其数学期望E(X)作为供货时间进行分析.

4 模型建立与求解

图1

商家存贮销售的商品为m种，就某种商品i而言，其循环过程中的损失费用分析如下：商品的存贮与销售是一个周期的循环过程，故可以就其中一个周期进行分析，商家商品的库存量变化情况如图（1）所示.现将商品的周转周期T分为几个不同的阶段，因各阶段库存商品数量的变化规律不同而导致损失费用变化规律不同，故首先对每个阶段进行分析，分别得出损失费用随商品数量变化的规律，以期通过各阶段损失费用的累加获得整个商品周转周期内损失费用相对商品数量变化的函数.将m种商品中每一种商品采取同样方法进行分析，然后把所有商品的损失费累加即可求得m种商品在一个存储周期存贮销售过程中总的损失费用[1,2,3].

4.1.1 由于商品的销售以体积(rivi)的方式减少，为了方便表述，在此依据上面的思路，定义第 种商品的库存减少速率（销售）为ki，

4.1.3 待货阶段：此阶段商家库存第i种商品数量为Li,为保证正常销售，商家开始订货，但所订货物不能立即到货，故此阶段中，商家卖出自己库存商品，其间损失为商品在自己仓库中的存贮费用：

4.1.4 缺货阶段：此阶段中商家库存商品已售完，预定商品尚未到货，因此，商家此时的损失费用为缺货损失费：

4.1.5 货物库存充盈阶段：在此阶段，商家预订商品已经到货，分别存入自己的仓库和租借的仓库，销售开始正常进行，因要节省费用，故租借仓库中的商品优先出售，至租借仓库中商品售完.此时，商家的损失费用为商品在仓库中的存贮费用.

卖租借仓库中商品时自己仓库的存贮费用：

4.1.6 准备订货阶段：在此阶段，租借仓库中的商品已出售完毕，开始出售自己仓库中所存商品，并在库存降至L i时开始订货，而后进入待货阶段，开始新的循环周期.此阶段中，商家的损失费用为商品在自己仓库中存贮的费用为：

4.1.7 在一个周期中的损失费用为各阶段损失费用的累加.一个周期内的总损失费用：

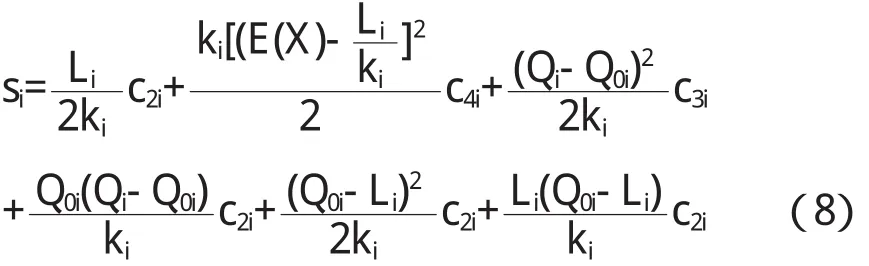
4.1.8 因商家现有m种商品，所以在周期T内总的损失费用为：

4.1.9 现同样以一段时期内商家总损失费用作为最终研究对象，设这一时期为整体1，则总体损失费用为：

4.2 模型的建立

在此将m种商品在一段时间内的总体损失费用最小作为追求的目标，建立模型.

目标函数：min Z

4.3 模型求解

此模型为有等式约束的极值问题，根据优化理论[4]，现采用两种方法对模型进行求解，以保证求解正确性.

4.3.1 拉格朗日乘数法求解

引入拉格朗日函数

对Qi,Q0i,Li(i=1,2,3…m)，λj(j=1,2)分别求导，并令其等于0可得方程组如下：

解以上方程组即可求得模型的最优解.

4.3.2 惩罚函数法求解

4.3.2.1 惩罚函数的引入

引入C o u r a n t罚函数如下：

这就将原模型转化为无约束的极值问题：min p(x)

4.3.2.2 算法步骤说明

步骤一：选定初始点为x0；选取初始惩罚因子δ1>0（可取δ1=1），惩罚因子的放大系数c>1（可取c=10）；置k=1.

步骤四：置xk+1=c δk;k=k+1，转步骤二.

5 仿真计算

假设有三种商品同时订货，其中v1=0.05立方米，v2=0.04立方米，v3=0.10立方米，自己的仓库用于存贮这3种商品的总体积容量Q0=6立方米，每次到货后这3种商品的存贮量总体积补充到固定体积容量Q=10立方米为止，且该供应站从接到订货通知到货物送达商场的天数X服从在1天到3天之间的均匀分布.其余数据同问题2中相应的商品中所列出的数据.按本文给出的模型求出这3种商品的最优订货点L*和自己的仓库用于存贮这3种商品的各自体积容量Q0i(i=1,2,3)以及在订货到达时使这3种商品各自存贮量补充到的固定体积Qi(i=1,2,3).(注：问题2参见2005年全国部分高校研究生数学建模竞赛B题中的问题2)

采用惩罚函数法来求解，依据上述算法，编程计算，迭代结果收敛于下表所示的数据：

Q1 5.29506Q01 4.203582L*1 0.610622Q2 1.76502Q02 0.673542L*2 0.826727Q3 2.94170Q03 1.12257L*3 2.50691

目前，许多商家为了满足市场的随机大量需求，采用租赁别人容量有限的仓库的方法.为降低不利损耗提高企业效益，必须采用有效的库存管理方法.仿真数据表明：通过求解本文建立的模型，可以较好地解决多种商品在允许缺货条件下的最佳订货点确定的问题.

〔1〕李温红.仓库容量有限条件下的不允许缺货存储模型[J].系统工程理论方法与应用，1997，6(3)：68-71.

〔2〕杨益民.仓库容量有限条件下的生产销售存储模型[J].系统工程，2001，19(1)：18-23.

〔3〕钱颂迪.运筹学[M].清华大学出版社，1990.369-385.

〔4〕袁亚湘，孙文瑜.最优化理论与方法[M].科学出版社，1997.

O227

A

1673-260X（2010）03-0008-03