基于提升小波算子的MUSIC法的DOA估计

(江苏省电子产品装备制造工程技术研究开发中心，江苏 淮安 223003)

1 引 言

DOA的估计一直都是移动通信、雷达、水下通信等方面的研究重点，有着极其重要的应用。而本文选用的MUSIC法是子空间DOA估计的经典算法之一，是一种分辨率较高的算法[1]。但这种方法在阵元数少、信噪比低或小样本支撑条件下会有较大的估计误差，且在分辨率上性能也会下降[2]。当前，将小波变换用于阵列信号处理在国内外已经变成研究热点。在高噪环境且不增加阵元数目的条件下，传统小波算子可以利用小波多分辨分析法，将分解出的子带进行DOA的估计，可以得到较高精度的DOA估计,但其算法复杂度和计算量很大，不适合信号的实时处理。针对此问题，本文提出了基于提升小波算子的MUSIC法对DOA的估计，该方法最大的优势在于，通过分解、预测、更新三个过程，对DOA估计性能达到更优。相比传统小波算子，实验结果证明，其计算复杂度要低很多，收敛快，且DOA估计的精度也有所提高。

2 MUSIC算法的经典模型

设有K个信号入射到阵列上，则N元阵列接收到的输入数据向量可以表示为K个入射波形与噪声的线性组合，即：

(1)

具体针对MUSIC算法的论文很多，本文不对该算法的过程进行具体阐述，可以参考文献[1]，本文只给出最后空间谱的表达式，如下：

(2)

在非相关的相同噪声环境下，找出PMUSIC(θ)的峰值对应真实的波达方向。然而，当入射信号在低信噪比环境下或低噪但信源角度间隔相差不大时，MUSIC分辨率会下降，从而影响DOA分辨的性能。因此，本文提出的基于小波子带的DOA估计大大提高了DOA的分辨率。

3 基于小波子带的DOA估计算法

对接收信号u(t)通过子带分解滤波器进行采样，将信号输入到一个M个子带滤波器中，将M个子样进行抽取，则第M个子带信号可以表示如下[3-4]：

(3)

当满足：

(4)

其中，Im为子带。

(5)

Im的全集即构成空间-π,π，且Im之间相互正交。

由于噪声表现为高频信息，而有效信息表现为低频信息，将得到的经过采样后的接收阵列信号y(k)的子带进行小波分解，得到平滑的近似信息和细节信息，因此得到的滤波矩阵可以表示如下：

yk(n)=HAs(n)+nh(k)=

(6)

其中：

(7)

即为阵列的近似信息和细节信息，利用小波的多分辨分析，可以将高频信息滤除。得到重构后的信号为

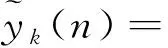
(8)

存在问题：上述算法是基于傅里叶变换的小波多分辨分析算法，该算法复杂度高，计算量大，不适合硬件的实现，在工程上实现有一定的难度。

4 提升小波的原理和应用

4.1 提升小波算法的应用

针对于以上问题，本文在以原有基于子带分解的MUSIC算法不足的基础上，提出基于提升小波算法的DOA估计。

提升小波在1996年由Sweldens[5，6]提出后，被认为是构造第二代小波变换的优质小波算法，目前该提升小波算子在信号处理领域得到了广泛应用，特别是在图像处理[7]和一维信号的去噪方面。

4.2 提升小波处理的阵列信号模型

图1 提升小波处理阵列信号的示意图
Fig.1 The array signal processing by lifting wavelet

提升算法的基本思想是，将现有的小波滤波器分解成基本的构造模块，分步骤完成小波变换。如图1所示，信号处理的过程分为3步。

(1)分解

将阵列信号u(t)经过抽样后得到离散阵列信号：

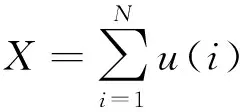
(9)

式中，N为快拍数。

本文令X的原始序列集为X(i)，将X(i)根据奇偶性均分为2个较小的子集X(i-1)和d(i-1)，其中d(i-1)为懒小波子集。

分解过程可以表示如下：

F(X(i))=(X(i-1),d(i-1))

(10)

式中，F(X(i))表示为X(i)的分解过程。

(2)预测

将偶数序列X(i-1)的预测值P(X(i-1))去预测奇数序列，将滤波器P(X)对偶数信号的处理转化为对奇数信号的预测。奇数信号实际值d(i-1)与预测值的误差表示为

d(i-1)=d(i-1)-P(d(i-1))

(11)

将X(i)重复n次迭代得到，我们可以得出，经过n步后的信号集可以表示为

{X(n),d(n),X(n-1),d(n-1),X(n-2),

d(n-2)，…，X(1),d(1)}

(12)

(3)更新

为了确保原有信号X的特性Q(X)不变，即要Q(X(i-1))=Q(X(i))，可利用已有小波子集d(i-1)对X(i-1)进行更新，从而保证特性参数Q(X)不变。采用更新算子U去更新，更新规则如下：

d(i-1)=d(i-1)+U(d(i-1))

(13)

从以上三个步骤可以得出，每个点都可以运用新的数据集根据式(12)代替原有的数据集X(i)。利用提升滤波器可获得小波的交织系数。

信号X(i)通过以上过程的分解，利用滤波器可以分离高低频信号，从而得到信噪比较高信号。

通过以上数学的描述可以看出，本文利用提升小波的优点，与传统小波进行信号分离的方法相比，该提升小波不依赖于傅里叶变换，小波变换后的系数是整数，与传统的基于卷积的离散小波变换的离散小波相比，其具有计算复杂度低、计算量小、速度快、精度高的优点。

5 仿真实验以及结果分析

5.1 单信号DOA的误差的仿真试验

通过单信号DOA的误差比较，验证基于小波域MUSIC算法的优点。

通过单信号的DOA误差仿真试验，可以测定在不同SNR下单信号的DOA的误差。用MUSIC算法接收单信号，通过在传统MUSIC法以及小波域内的MUSIC法对同样的单信号进行接收，并通过误差计算，可以测定出各个算法优劣。

(a)小波处理前

(b)小波处理后图2 不同信噪比下单信号的误差Fig.2 The error of a simple signal under different SNR

通过对单信号的精度仿真可以看到，在通信环境较差，即信噪比较低的环境下，经过小波域处理后，单信号的DOA精度要远大于直接接收的单信号的精度；在通信环境较好的情况下，小波域内的接收的信号精度和MUSIC法相差不大。因此，在一定程度上，小波域内的信号接收，提高了DOA估计的精度。

5.2 相邻角度分辨率的测定

在阵元数目较少情况下，相邻角度的分辨往往比较困难，常常要在高信噪比的环境下才能精确分辨。

通过具有相邻角度的两个信号的DOA的仿真，仿真试验采用3种算法，即：传统MUSIC法、基于小波域的MUSIC法接收、基于提升小波法的MUSIC接收，通过3种算法比较，可以比较出各个算法的优劣。

图3表明，在SNR=14 dB环境下，无法分辨5°、7°两个角度，Matlab中显示只有一个拐点，因此，传统MUSIC法在8阵元条件下，不能将5°、7°分辨开来。在SNR=15环境下，可以分辨5°、7°两个角度，Matlab中显示有两个拐点，因此，传统MUSIC法在8阵元条件下，能将5°、7°分辨开来。Matlab仿真的时间消耗为0.95 s。

(a)SNR=14 dB

(b)SNR=15 dB图3 传统MUSIC法对DOA的估计Fig.3 DOA estimation with traditional MUSIC algorithm

图4表明，在SNR=14环境下，可以分辨5°、7°两个角度。Matlab仿真的时间消耗为1.25 s。

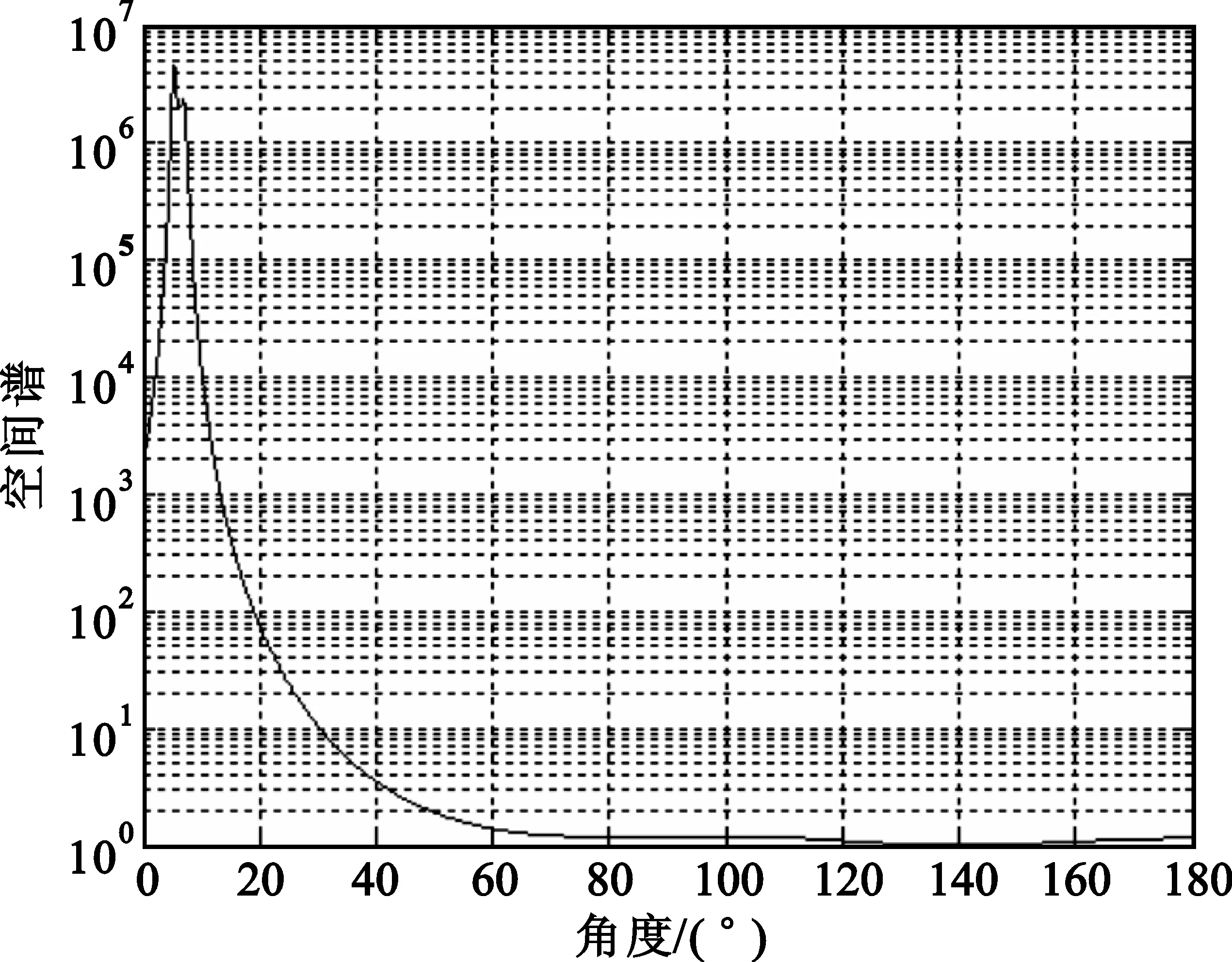
图4 基于小波域的MUSIC法的估计Fig.4 Estimation of MUSIC algorithm based on wavelet

图5表明，在SNR=12环境下，可以分辨5°、7°两个角度。Matlab仿真的时间消耗为1.05 s。

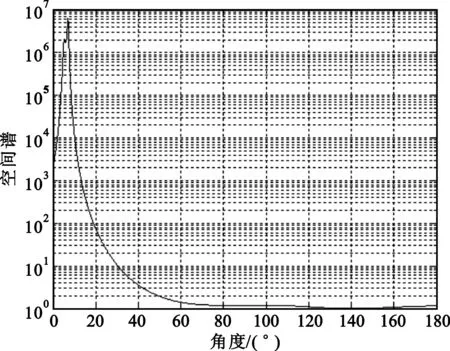
图5 基于提升小波法的MUSIC法的估计Fig.5 Estimation of MUSIC algorithm based on the lifting wavelet method

5.1节已经说明，在高信噪比条件下，传统MUSIC和基于小波域的MUSIC法的估计法的性能相差不大。通过5.2节可以看出，基于小波域的MUSIC法的估计法必须在信噪比为14 dB条件下才可以分辨，甚至，传统的MUSIC法则需要在信噪比为15 dB条件下才能分辨，而基于提升小波法的MUSIC法在信噪比为12 dB的环境下已经可以将5°、7°。通过各个仿真试验的Matlab仿真时间对比看出，传统MUSIC法需要0.95 s，基于小波域的MUSIC法需要1.25 s，而基于提升小波法的MUSIC法则需要1.05 s。相比传统MUSIC法，选用小波域法进行处理数据，必然会增加算法的复杂度和计算时间，而基于提升小波法的MUSIC法，算法复杂度相对来说较低，且收敛速度快，精度高。

5.3 多信号接收的误差仿真

在多个目标信号同时接收的情况下,研究在不同信噪比条件下，利用这3种算法，即传统MUSIC法、基于小波域的MUSIC法接收、基于提升小波法的MUSIC接收，通过多个信号接收的平均误差比较，可以比较出各个算法的优劣。

图6为在不同信噪比环境下，传统MUSIC法的接收，选用30°、60°、90°、120°的平均误差为指标进行仿真。在SNR=30 dB左右时，平均误差近似为0.075，Matlab计算所耗时间为0.657 0 s。

图6 4个信号的传统MUSIC法的平均误差Fig.6 The average error of the four signals by traditional MUSIC algorithm

图7为在不同信噪比环境下，基于小波域的MUSIC法的接收，选用30°、60°、90°、120°的平均误差为指标进行仿真。且在SNR=28 dB左右时，平均误差近似为0，Matlab计算所耗时间为0.922 0 s。

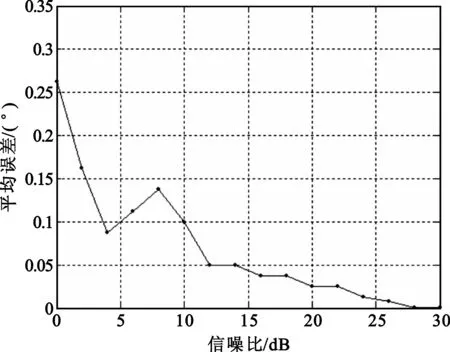
图7 4个信号的小波域的MUSIC法的平均误差Fig.7 The average error of the four signals by MUSIC algorithm based on wavelet

图8为在不同信噪比环境下，基于提升小波的MUSIC法的接收，选用30°、60°、90°、120°的平均误差为指标进行仿真。Matlab计算所耗时间为0.812 0 s。

图8 4个信号的提升小波法的MUSIC法的平均误差Fig.8 The average error of the four signals by MUSIC algorithm based on lifting wavelet

图6～8说明，相比另两个算法，在同样信噪比下，基于提升小波的MUSIC法具有更高的精度，且算法运行时间比基于小波域的算法短，更加适合硬件实现，对实现信号DOA实时性估计有着重要的意义。

5.4 小 结

通过以上仿真可以得出如下结论：

(1)在信噪比较低时，基于小波域的MUSIC估计算法比传统MUSIC算法的精度要高；

(2)在阵元数目较少的情况，即使处于高信噪比条件下，传统MUSIC算法对相邻角度的分辨仍然有限；基于小波域的MUSIC法在一定程度上提高了相邻角度分辨的性能，但算法复杂性增加很多；而基于提升小波法的MUSIC法既提高了算法性能，在分辨率上又有较大提高，且算法收敛较快；

(3)多个接收信号的DOA的平均误差中，基于提升小波的MUSIC法要优于传统MUSIC法和基于小波域的MUSIC法，且算法计算量小，更加适合硬件实现，对实现信号DOA实时性估计有着重要的意义。

6 结 论

本文提出了一种新的DOA估计算法，将提升小波算子成功应用到DOA估计的算法中。新算法利用小波多分辨分析的特点，提高了DOA的分辨率。同时，提升小波算子的特性得到重要应用，算法计算量比传统的小波算子大大降低，且精度比传统小波算子更高，为未来第四代移动通信技术提供了一种非常重要的信号处理手段，具有一定的理论价值和现实意义。

参考文献：

[1] KAVEH M, BARABELL A. Statistical performance of the MUSIC and minimum-normal algorithms in resolving plane waves in noise [J]. IEEE Tranactions on Acoust, Speech, Signal Processing, 1986,ASSP-34(2): 331-341.

[2] 樊祥， 程正东， 马东辉， 等. 两信号源的相关性对MUSIC算法分辨性能的影响[J]. 电子学报, 2008,36(12)：2315-2318.

FAN Xiang，CHENG Zheng-dong,MA Dong-hui,et al. Effect of Correlation of Two Signal Sources on Resolution Performance of MUSIC Algorithm[J]. ACTA Electronica Sinica,2008,36(12)：2315-2318.(in Chinese)

[3] SHU Xiang-lan, HAN Shu-ping. Improvement of DOA Estimation using Wavelet Denoising[C]//Proceedings of the 1st International Conference on Information Science and Engineering.Nanjing:IEEE,2009:587-590.

[4] 薛延波，汪晋宽,刘志刚，等.一种多分辨率 DOA估计的小波包算法[J].东北大学学报(自然科学版),2005, 26(7)：625-628.

XUE Yan-bo,WANG Jin-kuan,LIU Zhi-gang，et al. A Novel Multiresolution DOA Estimation Method with Wavelet Packet[J]. Journal o f Northeastern University (Natural Science), 2005, 26(7):625-628.(in Chinese)

[5] SWELDEN W.The lifting Scheme:A Custom-Design construction of Biorthogonal Wavelets[J]. Applied and Computational Harmonic Analysis,1996(3):186-200.

[6] SWELDEN W.The lifting Scheme:A construction of Second Generation Wavelets[J].SIAM Journal on Mathematical Analysis,1997,29(2)：511-546.

[7] Chang S G,Cvetkovic Z,Vetterli M．Locally Adaptive Wavelet-Based Image Interpolation[J]．IEEE Transactions on Image Proessing,2006，15(6):1471-1485.