基于MSN准则的自适应脉冲压缩修复处理
2010-09-26
(中国西南电子技术研究所,成都610036)
1 引 言
脉冲压缩技术通过发射一个具有大时宽带宽积的信号,在保证作用距离的同时获得了更好的距离分辨力。实现脉冲压缩的传统方法是采用匹配滤波器,它对于输入为单点目标加白噪声的情况,可以得到最大的信噪比。但是当大目标近邻距离单元有小目标时,大目标的旁瓣就会遮蔽其附近的小目标,从而影响小目标的正常检测。
为了解决大目标的旁瓣遮蔽邻近小目标的问题,已经提出过一些替代算法,包括时域加窗、频域加窗和LS算法。时域加窗[1]可以较好地抑制旁瓣,但是它需要对发射波形进行严格的调制,对发射机提出了更高的要求。频域加窗[1]可以依据所加窗函数做到旁瓣的抑制,但这种改善是以主瓣展宽为代价的。LS算法[2]在加性白噪声条件下是均方误差意义上最佳的,但是只要x(0)之前的N-1个距离单元中出现大的散射体就会对处理窗中的估计造成显著而且有害的影响。针对这种情况,Shannon D. Blunt 和Karl Gerlach提出了基于最小均方误差(MMSE)准则的迭代算法RMMSE[3],通过2~3次迭代可以将距离旁瓣抑制到噪声水平附近,大大改善了旁瓣抑制性能。利用这种迭代的思想,文献[4]提出基于最大输出信噪比(MSN)准则的RMSN算法,较之RMMSE其稳健性更好。
然而,很多在役雷达没有办法获取脉冲压缩前的接收回波,或者不能简单地更换已有的脉冲压缩系统,在这些情况下,以上提到的算法就不再适用。针对这种情况,Shannon D. Blunt 和Karl Gerlach又提出了脉冲压缩修复(PCR)[5]作为一种在匹配滤波器后抑制距离旁瓣的方法,算法对标准匹配滤波后的信号进行处理,获得了很好的旁瓣抑制。
结合RMSN算法和PCR算法,本文提出基于MSN准则的PCR算法。首先推导出算法的原理,其次给出了该算法的具体实现步骤,最后对单、多以及存在多普勒的目标进行仿真,以验证算法的适用性。
2 接收信号模型
因为算法要对匹配滤波器的输出信号进行处理,所以先从建立匹配滤波器信号模型开始。在数字域中,雷达照射的距离像可表示为与发射波形卷积的离散冲激响应,因此,接收回波的匹配滤波器输出可以表示为[5]
(1)
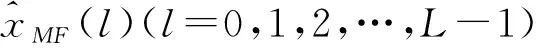
y(l)=xT(l)s+v(l)
(2)
其中x(l)=[x(l)x(l-1)…x(l-N+1)]T组成雷达实际冲激响应的样本,而v(l)是加性噪声。那么,匹配滤波器的输出可以写成:
(3)
其中:
v(l)=[v(l)v(l+1)…v(l+N-1)]T
A(l)=
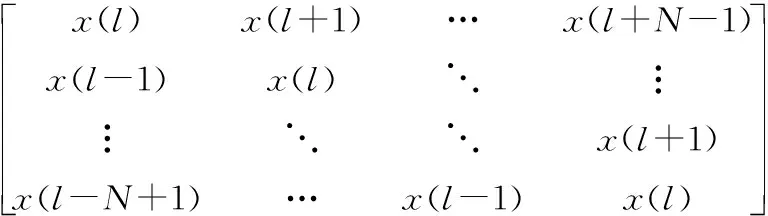
(4)
式中,A(l)是雷达冲激响应滑动采样组成的集合。
由式(4)可以看出,当A(l)对角线外部分中任何一个相对较大时通过匹配滤波器的估计都将受到影响,从而可能会引起距离旁瓣遮蔽较小目标。
将式(2)中发射波形和雷达冲激响应的卷积运算与式(1)中接收回波与时域反向、复数共轭波形的卷积运算合并,从而式(3)可以表示为
(5)
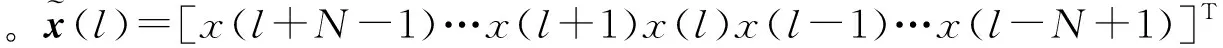
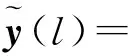
可表示为
(6)
其中:
B(l)=
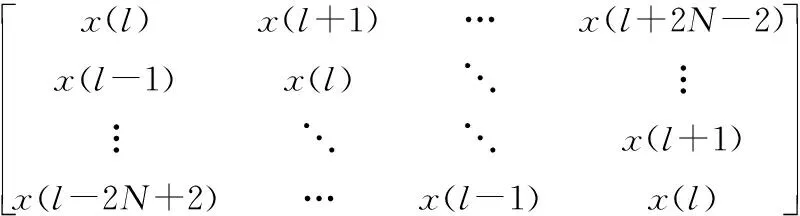
(7)
由式(7)可以看到对角线即当前距离单元的估计会受到对角线外,即其它距离单元的影响,因此将矩阵分解为对角矩阵B1(l)=x(l)I2N-1和非对角矩阵B2(l)=B(l)-B1(l)。式(6)可以重新表示为
(8)
式中,第一项为当前距离单元信号分量,第二项为近邻距离单元信号分量,第三项为噪声分量。在下一节将详细描述基于MSN的脉冲压缩修复滤波器。
3 基于MSN准则的脉冲压缩修复
为了实现对距离旁瓣的有效抑制,设计基于最大输出信噪比准则的滤波器w(l),对于每一个距离单元它都是特定的、不同的。经过w(l)滤波后,输出信噪比表示为
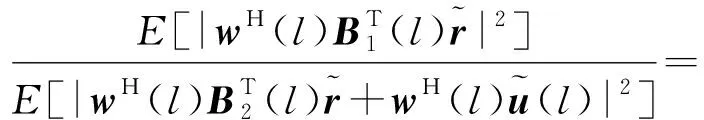
(9)
式中,
E[·]代表求期望。使式(9)输出信噪比达到最大的最优滤波器w(l)为
[Rc(l)+Rn]-1Rs(l)w(l)=λmaxw(l)
(10)
它是矩阵[Rc(l)+Rn]-1Rs(l)的最大特征值λmax所对应的特征向量。矩阵Rc(l)可定义为
(11)

(12)
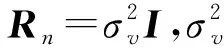
(13)
图1给出了两次迭代的脉冲压缩修复算法过程,其中下标用来表明迭代的次序。通常,递归脉冲压缩修复滤波器进行如下操作:
(1)采集匹配滤波器输出的信号样本,包括L长距离窗,及窗前的2M(N-1)个样本和窗后2M(N-1)个样本:{y(-2M(N-1)),…,y(L-1+2M(N-1))};
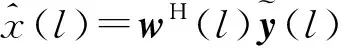
(4)重复步骤3,改成适当的标号,直到达到期望的L长距离窗。
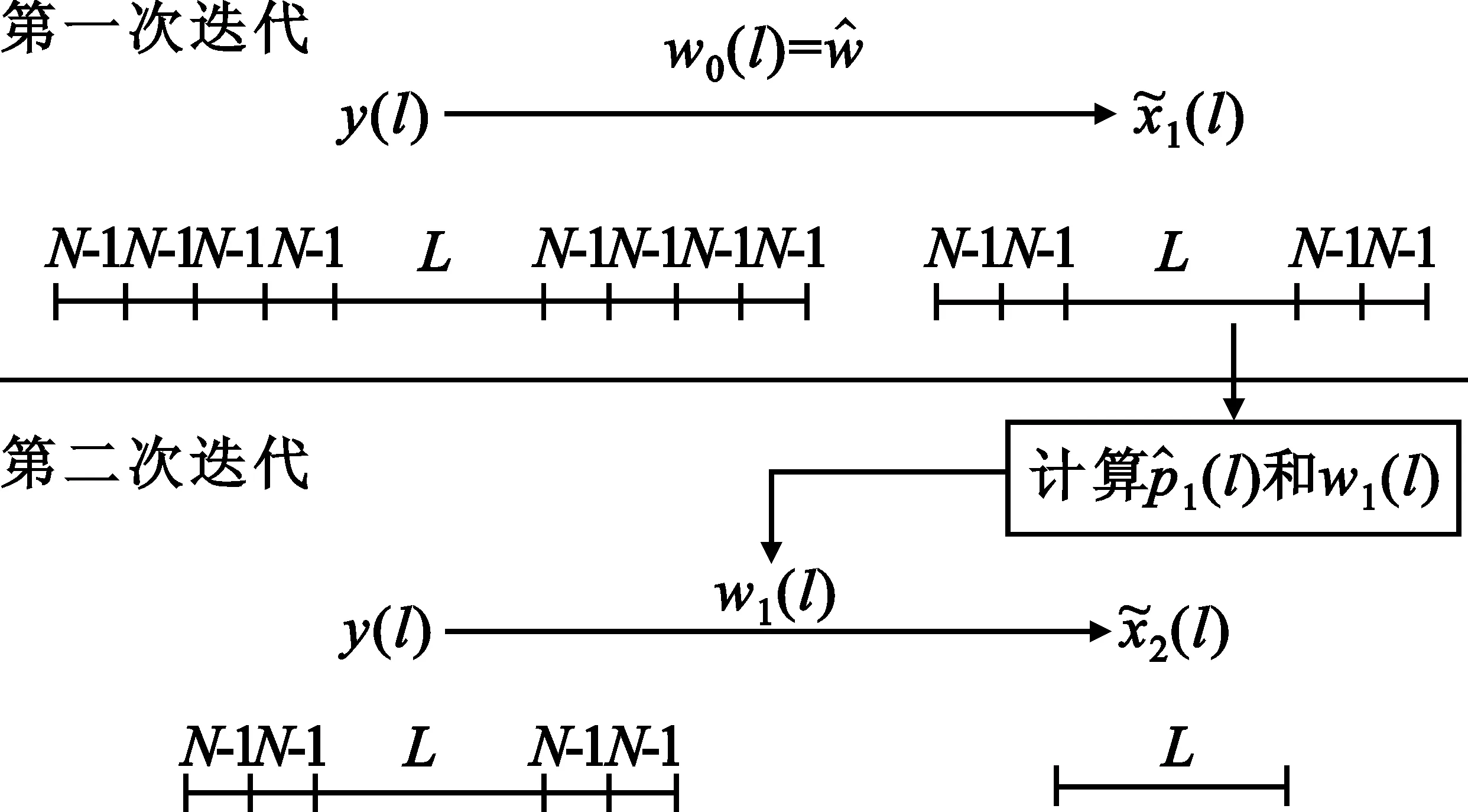
图1 算法过程示意Fig.1 Operation of the algorithm
从图中可以看出,每一个迭代阶段都要在距离窗外减少4(N-1)个距离单元估计,其中窗前2(N-1)个,窗后2(N-1)个,它们用来估计处理窗内的距离单元,并不是丢失了,而只是不再更新。所以,需要在距离窗的窗前和结尾各增加2M(N-1)个样本,M是迭代步骤的次数。
4 算法分析
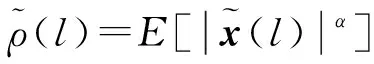
为了进一步优化算法,将式(10)变换可以得到:
Rs(l)-1[Rc(l)+Rn]w(l)=uminw(l)
(14)
式(12)两边求逆可得:
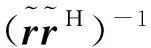
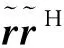
5 仿真结果
我们考虑4种情况来进行仿真,以验证算法的适用性和稳健性:单个大信噪比目标的提取;多个相邻目标的提取;单个大目标存在多普勒频移的情况;多目标存在多普勒频移的情况,并与匹配滤波器的输出进行比较。在4种情况下均采用脉宽10 μs、带宽5 MHz的LFM信号。噪声功率设为相对于最大目标-70 dB。匹配滤波输出进行归一化处理。
(1)假设在距离窗口中第51个距离单元有一个0 dB的目标,图2显示脉冲压缩修复算法通过两个阶段就可以收敛到真实的目标距离像。初始阶段即为标准匹配滤波器输出结果,也是修复算法所要处理的信号。第一阶段已经大大抑制了旁瓣,第二阶段则可以使旁瓣减小到噪声水平,形成“钉”形的目标估计。

图2 单目标,无多普勒Fig.2 Single target without Doppler
(2)假设在距离窗口中距离单元28、36、51、78、109各有一个目标,大小分别为-24 dB、-46 dB、0 dB、-34 dB、0 dB。图3给出了经过匹配滤波、一次迭代、二次迭代得到的目标估计。第一次迭代已经将旁瓣抑制到-50 dB左右,第二次迭代进一步将旁瓣抑制到噪声附近,小目标得以清晰地提取出来。相对匹配滤波器来讲,有了约50 dB的改善,大大提高了对大目标邻近的小目标的检测能力。

图3 多目标,无多普勒Fig.3 Multiple targets without Doppler
(3)为研究多普勒失配对算法的影响,对单、多目标分别进行分析。对于情况1,在目标的波形加上3°的相移。这个相移相当于速度为1马赫的目标被1 μs的S频段脉冲照射的情况。图4给出了仿真结果,可以发现由于多普勒的存在,引起了主瓣的展宽,以及旁瓣抬升10 dB左右,但是算法效果仍比匹配滤波提高了近40 dB。通过多次仿真发现,这个影响随着多普勒的增大而增大,随多普勒的减小而减小。

图4 单目标,有多普勒Fig.4 Single target with Doppler
(4)对于存在多普勒频移的多目标,目标存在情况与情况2相同,同时设置各目标存在-3°~3°之间的随机多普勒频移。图5显示经过两次迭代,主瓣展宽,同时引起旁瓣抬升20 dB左右,但是仍然可以清楚地显示出各目标的位置。同样,这个影响随着多普勒的变化而成正比变化。
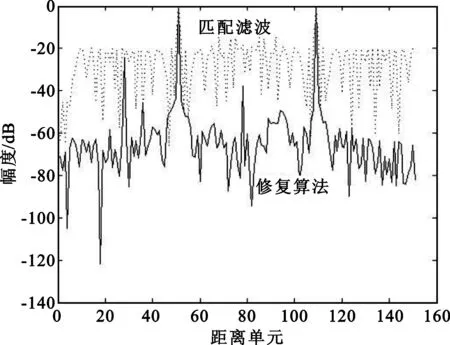
图5 多目标,有多普勒Fig.5 Multiple targets with Doppler
6 结 论
基于最大信噪比准则的自适应脉冲压缩算法,得到了良好的旁瓣抑制性能,但是对于很多在役雷达系统不能更换已有的脉冲压缩设备,这种算法就不再适用。本文提出的修复算法则把匹配滤波结果看作接收信号来处理,以抑制距离旁瓣。通过仿真发现,算法可以将旁瓣抑制到噪声附近,提高了对小目标的检测能力。当存在多普勒频移时,算法性能有所下降,表现为主瓣下部展宽,旁瓣肩比无多普勒时有所抬升,但较之匹配滤波仍然有很大性能提升。未来研究的方向是该算法在杂波环境下的适用性和性能分析。
参考文献:
[1] Mark A Richards. 雷达信号处理基础[M].北京:电子工业出版社,2008.
Mark A Richards. Fundamentals of Radar Signal Processing [M]. Beijing: Publishing House of Electronics Industry, 2008. (in Chinese)
[2] Zric B,Zejak A. Rang sidelobe suppression for pulse compression radars utilizing modifies RIS algorithm [C]//Proceedings of IEEE Spread Techniques and Applications.South Africa:IEEE, 1998: 1008-1010.
[3] Blunt S D, Gerlach K. A novel pulse compression scheme based on minimum mean square error reiteration [C]//Proceedings of IEEE International Conference on Radar.[S.l.]:IEEE, 2003: 349-353.
[4] 张劲东,王海青,朱晓华,等. 基于最大输出信噪比准则的自适应脉冲压缩[J].电子与信息学报,2009,31(4):790-793.
ZHANG Jin-dong, WANG Hai-qing, ZHU Xiao-hua, et al. Adaptive Pulse Compression via MSN Criteria [J]. Journal of Electronic & Information Technology,2009,31(4):790-793. (in Chinese)
[5] Gerlach K, Blunt S D. Adaptive radar pulse co-mpression repair processing[C]//Proceedings of 2005 IEEE International Conference on Radar.[S.l.]:IEEE,2005:519-523.
