基于长游程二次编码的测试数据压缩方法
2010-09-25于海涛程晓旭
于海涛,程晓旭,李 梓
(大庆师范学院 计算机科学与信息技术学院,黑龙江 大庆 163712)
0 引言
随着超深亚微米技术的广泛应用,集成电路的尺寸变得越来越小,而芯片内部的结构变得更加复杂,一个芯片上可能集成数亿个晶体管,芯片的复杂性和测试数据量的不断增加使得芯片的测试费用不断上升,而测试数据量也变得越来越庞大。一方面,需要测试设备具有较大的存储容量来存储测试数据,另一方面将测试数据从测试设备传输到测试芯片需要更多的测试通道[1]。所有这些问题,如果仅通过更大容量、更高频率的测试设备来解决,必然会造成测试成本的巨幅增加。因此,单纯地提高测试设备的性能并不是一个好的解决方案,而探索高效的、快速的测试技术无疑是解决这些问题的重要途径。提高测试数据压缩技术是解决这一问题的有效手段,是近年来大量学者们广泛关注的热点,其中编码方法是测试数据压缩的主要技术之一。编码方法主要有Run-length[2],Golomb编码[3],FDR码[4]和Variable-tail编码[5]等。
Run-length 编码方法对于游程长度特别大的串进行编码时,需要进行分组,例如码字长度为3的Run-length 编码,最多有23=8个编码字。如果测试向量中的游程长度大于8,就需要分组进行编码。此时的压缩效果不是很理想;Golomb编码则是变长-变长的编码,对于游程长度没有限制,不需要对长游程的串进行分组。但是这种编码方法的缺点是每个前缀所对应的编码字的个数不变。所以前缀不能得到有效的利用;FDR码是一种变长-变长的编码,但是该种编码的尾部是变长的,尾部的长度等于头部的长度,因此每个前缀对应编码字的个数随着前缀长度的增加而增加;Variable-tail编码也是基于游程的编码技术,每组编码的后缀不相同,并且一次增加一位,所以每组包含的编码字总是上一组所含编码字数的2倍。该种编码中每组的编码字都比上组的编码字多两位,所以随着组号的增加,每组所包含的编码字的数量增加很快,呈指数级增加速度。因此前缀得到有效的利用。使用以上这些方法,长游程的压缩率不是很高,因此本文针对长游程编码字,进行二次编码压缩,从而进一步提高了长游程的编码压缩率。
1 长游程二次编码的压缩方法
通过研究提出了一种长游程编码进行二次编码的方法,通过该方法使得长游程的编码得到了进一步的压缩。
1.1 预处理
在进行压缩之前,首先应对测试集合进行如下过程预处理:①对测试向量中的无关位X进行处理和相容的测试向量的合并;②对测试向量进行排序;③对测试向量进行差分变换。
1.1.1 对无关位进行处理和相容测试向量的合并
大量的实验表明测试向量中存在大量的无关位X, 无关位取0或取1不影响故障的覆盖率。我们对无关位进行赋值的原则是尽量增加游程0的长度,从而起到增加压缩率与减少测试功耗的目的。两个测试向量相容,是指两个测试向量对应位相同,或者至少其中一位为无关位。通过相容测试向量合并能够减少测试向量的数量。
1.1.2 测试向量进行排序
鉴于测试向量之间不同数值位较少的事实,为了获得更高的压缩率,我们需要把原始的测试向量集进行排序,经过排序的测试向量集合中相邻的测试向量的海明码距最小。排序的方法利用图论中的Hammilton图[5]的方法。实现过程:设完全有向图G=(V,E),节点vi∈V表示S的测试向量,每一条边(vi,vj)∈E,表示测试向量对。边上的权值表示向量之间的海明码距,然后我们找到一条路径,使得边上的权值和最小,这类似于Hammilton的旅行商问题。求解该问题是一个NP问题,我们利用贪婪算法可以解决这一问题,该方法虽然不能得到最优解,但是得到的解接近最优解[6]。
1.1.3 向量的差分变换
由于经过排序的测试向量之间数值位的差别较少,所以把经过排序的测试向量集合TD转换为差分向量序列Tdiff={t1,t1⨁t2,t2⨁t3…..tn-1⨁tn},经过差分变化后Tdiff中的差分向量就含有较多的0位,这样有利于进行“0”游程长度的编码,编码的压缩效果比较好。
1.2 一次编码
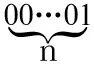
1.3 进行二次编码的压缩方法
设表1共有2n个游程编码字,我们对前n个编码字保持不变,而对后n个(n+1)~2编码字进行重新编码,将它们编码为以0为前缀的编码字。编码的方法如下:
第n+1个编码字为010(01为前缀) 第n+2个编码字为011(01为前缀)
第n+3个编码字为00100(001为前缀) 第n+4个编码字为00101(001为前缀)
……
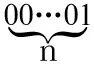
例如某个测试集合中最大的游程长度为26,如果按照游程压缩编码方法进行编码,那么从第14~26个(即按照游程长度进行升序排序,排在后50%的游程)游程长度的编码字分别为:111100000,111100001,111100010,111100011,111100100,111100101,111100110,111100111,111101000,111101001,111101010,111101011,111101100,编码的长度都为9。那么经过二次编码后的编码为:010,011,00100,00101,00110,00111,0001000,0001001,0001001,0001010,0001011,0001100,0001101,那么经过二次编码后的长度的减少为:9-3=6,9-3=6,9-5=4,9-5=4,9-5=4,9-5=4,9-7=2,9-7=2,9-7=2,9-7=2,9-7=2,9-7=2,9-7=2。减少的总长度为:6*2+4*4+2*7=42。减少的百分比为42/(9*13)=35%。随着游程的最大长度的增加,压缩的百分比也会增加。
2 解压缩算法与解压缩电路的设计
2.1长游程二次编码的解压缩算法
解压算法如下:
①输入压缩编码;
②读取前缀,如果前缀为一连串的1与表示结束标志的0字组成,那么按照如下方法解压缩,否则转向③;
i)求出前缀的长度Lpre,确定编码所在的组,所在的组号=Lfirst-1,该组的第1个编码字所对应的编码字的游程长度为Lfirst=2Lpre-1-2;
ii)根据前缀的长度Lpre,读取相应的后缀,后缀的长度=Lpre-1,后缀即为该编码在该组中的相对位置Lpos,游程长度Llen=Lfirst+Lpos;转向④;
③如果前缀为一连串的0与表示结束标志的1字组成,那说明该编码字是经过二次压缩的编码字,按照如下步骤进行解压:
i)求出前缀的长度Lpre,确定编码所在的组,所在的组号=Lpre-1,该组的第1个编码字所对应的编码字的游程长度为Lfirst=2Lpre-1-2;
ii)根据前缀的长度Lpre,读取相应的后缀,后缀的长度=Lpre-1,后缀即为该编码在该组中的相对位置Lpos,游程长度L’len=Lfirst+Lpos, 该长度值不是真正的游程长度值,因为此时的游程长度与实际的游程长度存在一个偏差n(n-L/2,L为最大的游程长度),所以实际的游程程度为Llen=L’len+n,转向④;
④输出Llen个0,然后输出一个1,该编码字解压解压结束;
⑤如果存在下一个编码字,读取下一个编码字并转向②,否则转向⑥;
⑥该测试向量的压缩编码解压结束。
2.2解码器电路
解码器的设计类似FDR解码器,它是基于有限状态机(FSM)的设计。该解码器的结构简单,电路规模小,只是增加了一个S_bit计数器,其中S=int(log2N)+1(int为取整函数)(N=L/2,L为最大游程长度)。图1为解码器框图。该电路由1个有限状态机,一个K_bit计数器,一个(log2K-1)_bit计数器,一个S_bit计数器。“bit-in”和“en”分别是位输入和使能信号,当有限状态机准备就绪时,输入编码数据。“counter_in”是到K_bit计数器的位输出,dec1控制计数器减1,rs1表明K_bit计数器复0状态。(Log2k-1)计数器用作识别后缀长度,信号”inc”和“dec2”分别控制计数器加1和减1计数。”rs2”指示完成计数。“dec3”和”rs3”分别用于计数器减1和标明计数器复0状态。
工作原理如下:
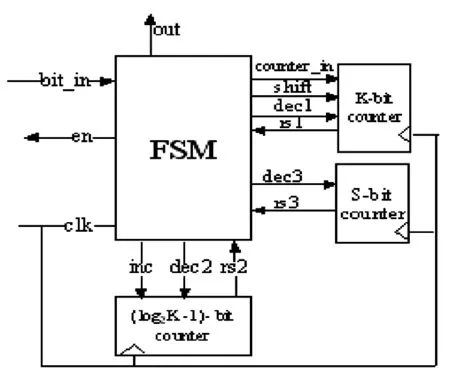
图1 解码器框图
1)首先,有限状态机发出使能信号“en”为1,然后“shift”和“inc”均为高电平,控制“bit_in”和“counter_in”移入前缀进入K_bit计数器,(log2K-1)_bit计数器加1(由于后缀比前缀少1位,所以当前缀为0时,就停止加1)。当“bit_in”为0时,前缀输入结束。如果输入前缀以1开始的,则编码没有经过2次编码,将0移入S_bit计数器(此时游程的偏移量为0),如果输入前缀以0开始的,则说明编码经过2次编码,将n移入S-bit计数器(此时游程的偏移量为n);
2)“dec1”为高电平控制计数器减1,out连续输出0,直至K_bit计数器为0。此时前缀解码结束;
3)然后S_bit的“dec3”为高电平控制计数器减1,out连续输出0,直至S_bit计数器为0。此时二次编码的解码结束;
4)接下来,输入后缀进入K_bit计数器,(log2K-1)_bit计数器控制后缀长度,“dec2”为高电平控制计数器减1,out连续输出0,当(log2K-1)_bit计数器为0,返回“rs2”高电平。后缀输入结束;
5)“dec1”为高电平控制计数器减1,out连续输出0,直至K_bit计数器为0,此时后缀解码结束。
3 实验结果
实验的硬件平台包括Intel P4 3.0G CPU,512M内存的PC工作站。编码算法是在PC工作站上完成的,测试向量数据是在SUN工作站上产生的,采用的MINTEST产生测试向量,这些测试向量对固定型故障的覆盖率均为100%。
我们先对测试向量先进行如下处理:相容合并、向量排序、差分变换。测试数据压缩率实验结果如表2所示。由表2可以看出,本文提出的方法使测试数据的压缩率得到了进一步的提高。在表中S13207电路的压缩率最高,原因是该电路中测试矢量集的长度最大,因此测试矢量之间的相关性比较高,经过排序和差分变换后,测试矢量中0的个数较多,所以导致长游程的比率较大,因此该电路的编码压缩率最高。相反S5378电路测试集合的长度最小,因此该电路的编码压缩率最低。

表2 测试编码压缩率的比较
4 结论
本文提出了一种长游程编码的二次编码的压缩方案,该方法是对经过一次编码后的编码字中编码字长度较大的编码进行了二次编码压缩,实验结果表明该压缩方法有效地提高了测试数据的压缩率。该方法的压缩率高,解压电路简单,硬件开销小,该方法对于长游程比率较高的测试数据的压缩效果较好。在今后的工作中,应重点进行增加长游程比率的预处理的研究工作。
[参考文献]
[1] A.Khoche, J.Rivoir.I/O bandwidth bottleneck for test:Is it real?[C]. USA:Proceeding International Workshop Test Resource Partitioning,2000: 231-236.
[2] A Jas and N.A. Touba. Test vector compression via Cyclical Scan Chain and Its Application to Testing Core-Based Designs[C]. USA:Proceedings of IEEE International Test Conference, 1998:458-464.
[3] Chandra A,Chakrabarty K.System-on-a-chip test data compression and decompression architectures based on Golomb codes[J]. IEEE Transactions on CAD of Integrated Circuits and System,2001,20(3):355-368.
[4] Chandra A,Chakrabarty K.Frequency—directed run length (FDR) codes with application to system—on—a—chip test data compression [C].USA :Proceedings of VLSI Test Symposium.Marina Del Rey,2001:2-47.
[5] 韩银河,李晓维.测试数据压缩和测试功耗协同优化技术[J].计算机辅助设计与图形学学报,2005, 17(6):1307-1311.
[6] 王健波,曾成碧,苗虹.减小数字电路测试功耗的方法—测试向量排序方法[J].四川大学学报:工程科学版,2000(6):89-91.
