希尔伯特-黄变换在谐波和间谐波检测中的应用

王海露

(滁州城郊供电公司,安徽滁州239000))

谐波是由于电力系统中某些设备和负荷的非线性特性所造成的波形畸变。如今,随着大量非线性电力元件的应用,电网中的谐波情况越来越复杂,不仅存在频率是工频整数倍的谐波,而且存在大量的非整数倍的间谐波,给电力系统的安全经济运行带来了危害,同时间谐波的存在也增加了谐波分析的难度。

现行国家标准《电能质量公用电网谐波》(GB/T 14549-1993)只对谐波规定了限值和测试方法。IEC-61000-2-2将间谐波定义为：在电压和电流信号的谐波之间存在频率与基波频率不成整数倍关系的信号。

电力系统中的谐波检测方法主要有基于傅里叶变换的谐波检测、基于瞬时无功功率的谐波检测、基于小波分析的谐波检测和基于神经网络的谐波检测方法等。基于傅里叶变换的谐波检测是目前应用最广泛的一种方法,使用该方法检测谐波,精度较高,使用方便,但存在频谱泄漏和栅栏效应[1]。

利用加窗、插值算法可以较好地消除频谱泄漏和栅栏效应,提高了非整数次谐波的检测精度,但该算法会导致谐波分辨率降低。小波变换因其良好的时频局部化特性,可用来分析谐波,通常利用连续小波变换(CWT)系数的幅值来检测谐波频率,但由于不同尺度的小波函数在频率中存在相互干扰,当被检测信号中含有频率相近的谐波分量时,无法将频率相近的谐波分离[2]。

希尔伯特-黄变换(Hilbert-Huang Transform,HHT)是近年来用于分析平稳和非平稳信号的新方法。与上述两种方法比较,该方法具有如下特点：

(1)通过EMD分解的信号展开,幅度和频率调制也被清楚地分开,从而打破了固定幅度和固定频率的傅里叶变换的限制,得到了一个可变幅度和可变频率的信号描述方法;

(2)EMD分解的基函数是一系列可变幅度和可变频率的正余弦函数,它是由信号分解中自适应得到的;

(3)基于信号局部特征的分解方法——EMD的引入使得瞬时频率这一概念具有了实际的物理意义,而且与频率的经典定义方法(信号相位的导数)相一致,从而可以给出信号频率变化的精确表达[3]。

1 希尔伯特-黄变换理论方法

对一列时间序列数据先进行经验模态分解,然后对各个分量做希尔伯特变换的信号处理方法,是由美国国家宇航局的Norden E.Huang于1998年首次提出的,称之为希尔伯特黄变换(HHT),该方法被认为是近年来对以傅里叶变换为基础的线性和稳态谱分析的一个重大突破。由于时间序列的信号经过EMD,分解成一组本征模函数,而不是像傅里叶变换把信号分解成正弦或余弦函数,因此,该方法既能对线性稳态信号进行分析,又能对非线性非稳态信号进行分析。

1.1 经验模态分解(EMD)

经验模态分解(EMD)方法能把复杂的信号分解成一组稳态和线性的数据序列集,即固有模态函数(intrinsic mode function,IMF)。所谓固有模态函数,必须满足2个条件：(1)对于一列数据,极值点和过零点数目必须相等或至多相差一点;(2)在任意点,由局部极大点构成的包络线和局部极小点构成的包络线的平均值为零。EMD算法的计算步骤叙述如下[4]：

步骤1：计算出信号s(t)所有的局部极值点。

步骤2：求出所有的极大值点构成的上包络线和所有的极小值点构成的下包络线,分别记为v 1(t)和v2(t)。

步骤3：记上、下包络线的均值为m11(t)=[v1(t)+v2(t)]/2,并记信号与上、下包络线的均值的差为h11(t)=s(t)-m11(t)。

步骤4：判断h11(t)是否满足IMF的上述两条性质。若满足,则 h11(t)为IMF;否则,记 h11(t)为s(t)重复步骤1～步骤3,直至得到一个IMF,记为c1(t)。

步骤5：记r1(t)=s(t)-c1(t)为新的待分析信号重复步骤1～步骤4,以得到第二个IMF,记为c2(t),此时,余项r2(t)=r1(t)-c2(t)。重复上述步骤,直至得到的余项rn(t)是一个单调信号或者成为仅有一个极点的函数时,分解结束。

如此,最终可得到n个IMF分量,c1(t),c2(t),…cn(t),余项为rn(t),因此,原始信号s(t)可表示为

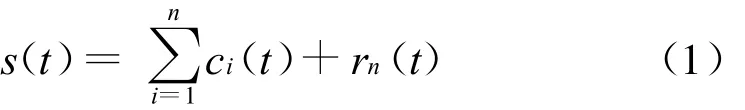
1.2 希尔伯特(Hilbert)变换

实信号X(t)的Hilbert变换定义为

其反变换为

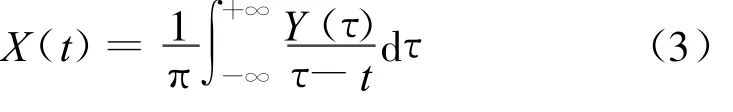
得到的解析信号为

式中,a(t)为瞬时幅值;θ(t)为相位;其表达式分别为

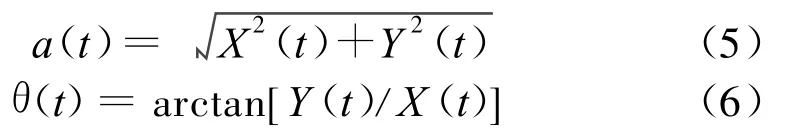
瞬时频率的计算公式为

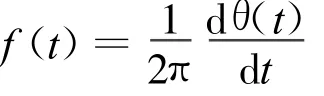
以上的EMD和与之相应的Hilbert变换的分析方法统称为Hilbert-Huang变换(HHT)。

2 谐波和间谐波检测步骤

含有谐波和间谐波的信号经EMD后得到一系列IMF,每个IMF为平稳的单频信号,在此基础上借助希尔伯特变换进一步得到信号的频谱图,因此基于IMF分量进行希尔伯特变换后的结果能够反映真实的物理过程,从而实现谐波和间谐波的检测。其检测步骤为：(1)对含有谐波的信号进行EMD分解,得到一组平稳的单频IMF分量;(2)对每个IMF分量进行希尔伯特(Hilbert)变换,得到解析信号;(3)利用式(5)～(7)得到每个模态分量的瞬时幅值和瞬时频率,实现对谐波和间谐波的检测。

3 算例仿真结果与分析

3.1 算例1

参照文献[5]的算例,设仿真谐波信号s(t)=2sin50πt+sin100πt+sin170πt+sin400πt,采样频率为6 400 Hz(每个工频周期采样128个点)。信号中含有基波信号和三个频率为25 Hz、85 Hz和200 Hz的谐波信号,其原始信号见图1。

现在对上面的信号进行EMD分解,得到4个单频的IMF 分量,c1、c2、c3和c4,以及余量r,见图2。从图2中,我们可以看出含有谐波的信号被分解成一组平稳的信号,c1分量的频率最高,而c4分量的频率最低,故而几个频率的信号经过EMD分解可以将其分解开来。

图2 EMD分解结果(算例1)

现对每个IMF分量做Hilbert变换,求其各IMF分量的幅值和频率,如图3、图4所示。HHT变换的结果见表1所示。

图3 IMF分量的幅值(算例1)

图4 IMF分量的频率(算例1)

表1 信号经HHT变换的结果

从图3、图4可知,EMD可以将信号准确地分解为一组稳定的单频分量,各分量就是信号中的各谐波成分,以及基波成分。从表1可以看出,HH T方法可以检测出谐波、间谐波的幅值和频率,准确度比较高。

3.2 算例2

设一仿真谐波信号为

采样频率为6 400 Hz(每个工频周期采样128个点)。信号中含有基波信号和三个频率为100 Hz、250 Hz和400 Hz的谐波信号,并且三个谐波信号的发生时间不相同,其原始信号见图5。对信号进行EMD分解,得到IMF分量,见图6所示。

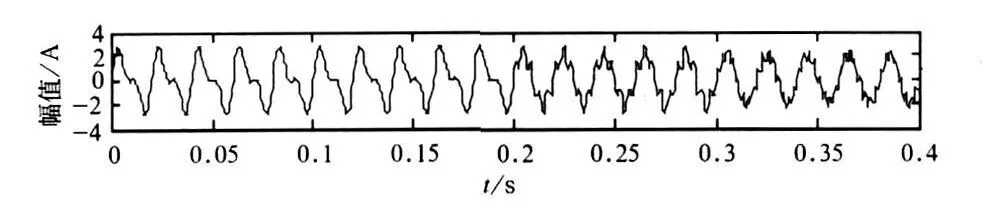
图5 原始信号(算例2)

图6 EMD分解结果(算例2)

从图6中,我们可以看出,c1包含2次、5次和8次谐波,c2是基波。在此基础上求出瞬时幅值和频率,如图7、图8所示。

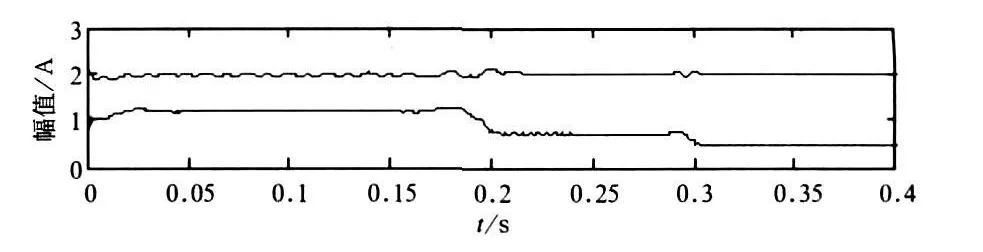
图7 IMF分量的幅值(算例2)

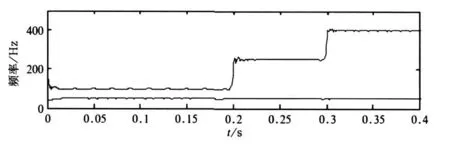
图8 IMF分量的频率(算例2)

从图7中,可以看出各次谐波的幅值、基波的幅值和原信号一致。从图8中,可以得知c1分量的频率包含了100 Hz、250 Hz和400 Hz,而且可以清晰地看出这三个频率的分界处(对应于0.2 s和0.3 s)。显然,HHT变换可以准确地检测出谐波发生、终止和突变的时刻。

4 总 结

在上面的仿真中,我们可以发现在端点处波形有略不规则现象,瞬时频率和幅值也会受到影响,这是由于在EMD分解过程中,首先要找出信号的极大值和极小值,并分别用两条包络线把极值连接起来,这时左右两个端点的包络线会出现所谓“端点飞翼”,造成分解结果发生偏差。端点问题正是EMD分解所存在的问题,也是大家所研究的重点,待解决的难题。

希尔伯特-黄变换方法用于非平稳、突变的谐波检测和分析,能够方便准确的通过EMD分解得到固有模态分量IMF,并测定各个谐波的瞬时频率和幅值,以及谐波发生、终止时刻,以及谐波突变时刻,与现有方法相比更为灵活、准确和有效,是电力系统谐波分析的一种新的有力工具。

[1] 张伏生,耿中行,葛耀中.电力系统谐波分析的高精度FFT算法[J].中国电机工程学报,1999,19(3)：63-66.

[2] 薛 蕙,杨仁刚.基于连续小波变换的非整数次谐波测量方法[J].电力系统自动化,2003,27(5)：49-53.

[3] 李天云,赵 妍,李 楠,等.基于 HHT的电能质量检测新方法[J].中国电机工程学报,2005,25(17)：52-56.

[4] 刘霖雯,刘 超,江成顺.EMD新算法及其应用[J].系统仿真学报,2007,19(2)：446-447,464.

[5] 赵成勇,何明锋.基于复小波变换相位信息的谐波检测算法[J].中国电机工程学报,2005,25(1)：38-42.