三相电压型PWM整流器控制新技术的研究

焦春雷,严登俊

(河海大学 电气工程学院,江苏 南京210098)

0 引 言

与传统二极管和晶闸管移相整流相比,三相电压型PWM 整流器具有网侧电流谐波低、功率因数高、能量双向流动及恒定直流电压控制等优点,符合“绿色电能变换”的要求,得到了广泛的应用和研究。但由于电压型PWM整流器模型是一个典型非线性多输入多输出系统,模型中含有状态变量和控制变量的乘积,并且状态变量间存在耦合,所以常规的控制策略难以满足快速动态响应、输入电流畸变小和单位功率因数的要求。现行用于该系统的控制策略主要分成两类：一类是间接电流控制;另一类就是目前占主导地位的直接电流控制。直接电流控制策略采用了交流电流内环、直流电压外环控制结构,具有网侧电流动态响应快易实现单位功率的优点;其不足是直流电压响应较慢、抗扰性较差。对此,本文根据电压型PWM整流器的数学模型,建立了整流器的直接电流控制数学模型,提出了基于电流前馈解耦控制的电压型PWM整流器控制策略,采用了dq坐标系下的电流内环、基于滑模控制电压外环的控制结构,而电流内环输出的控制信号则采用SVPWM技术调制。此方案实现了对有功电流和无功电流的解耦;提高了直流电压的响应速度和鲁棒性,增强了系统的抗扰能力。计算机仿真证明了该策略的可行性。

1 基于滑模控制的电压外环设计

图1为三相电压型整流器主电路拓扑图。

其中定义开关函数

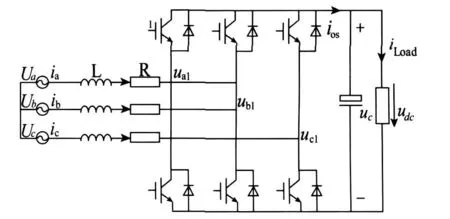
图1 三相Boost型PWM整流器主电路拓扑

则采用功率三相转同步dq坐标变换,三相PWM整流器dq模型[1]为

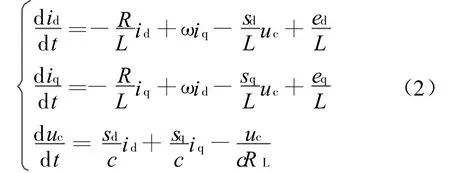
忽略输入电感损耗和三相整流桥路自身损耗,则三相空间矢量变换器交流侧有功Psa与直流侧功率Pdc相等,即

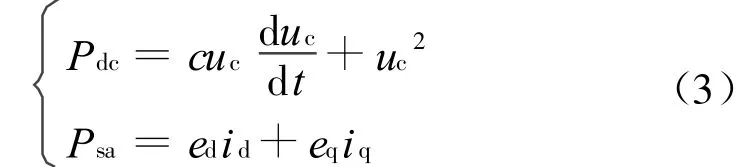
由式(1)的第三个方程可得

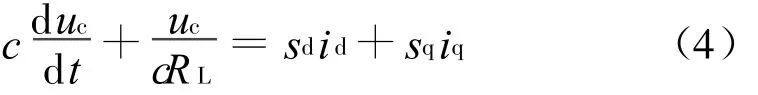
把式(3)和(4)联立,则式(2)第三个方程可改写为

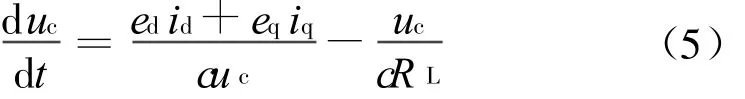
从式(2)和式(5)可以看出,该系统有两个控制量sd和sq。sd通常用来控制输出直流电压uc,sq用来控制无功电流i q以获得给定功率因数。故可以选取u c和iq为系统输出。定义误差变量 σ=[σ1σ2σ3]=[iLqiLq*u c-u c*u c],根据滑模控制理论[2],可选择滑模面s1(σ1,t)和 s2(σ1,σ2,t)为

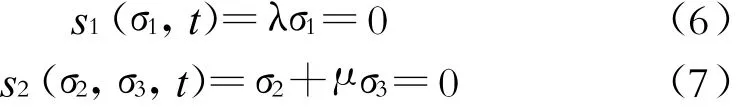
式中,λ,μ为反馈系数。

因此,通过设置以上滑模面及适当的反馈系数即可获得期望的动态响应和系统的稳定性及鲁棒性。理论上反馈系数μ越小,直流电压响应越快,但其不能太小,否则将激发系统未建模动态[3]。把式(5)代入式(7)可得

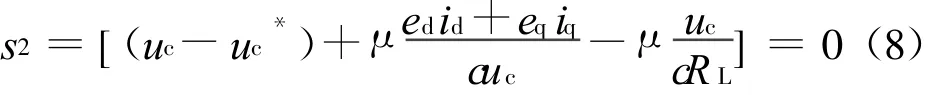
进一步变形式(8),可以得到

由于稳态时e q=0,则这时可以定义

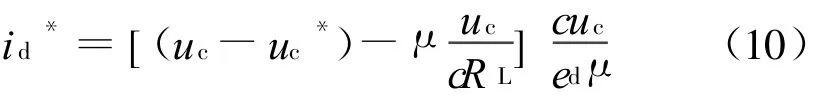
这里的i d*就是有功电流内环所需要的参考指令值,而系统的滑模面式(6)、(7)可重新定义为

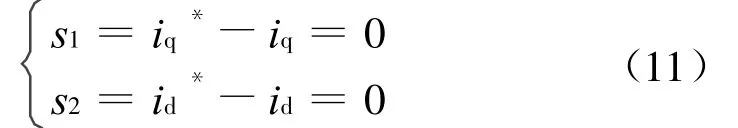
常规滑模控制在定义滑模面式(11)后[2],均采用滞环控制,由此带来开关频率不固定的缺点。因此本文仅采用滑模控制外环,以获得有功电流内环所需要的参考有功电流,即式(10),然后经电流内环控制后给出整流器的电压矢量指令,利用定频SVPWM技术即可实现开关的定频控制。

2 前馈电流解耦控制系统设计

根据式(1)前两个方程可得以i d,i q为变量的直接电流控制数学模型

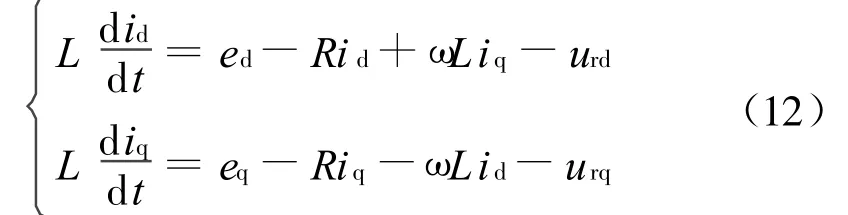
式中,u rd、u rq为整流器输入电压矢量(其中u rd=s d u c,urq=squc)。

由式(12)的两个方程可以看出,数学模型中的d轴和q轴是互相耦合的,因此无法对两方程单独控制,这对控制器的设计造成一定程度的困难。对一个耦合系统进行控制,工程上希望实现某一个输出量仅受某一个输入量的控制,这种控制方式称为解耦控制[4]。线性定常系统的解耦一般有串联补偿器实现解耦和前馈补偿器进行解耦,这里采用前馈解耦控制。为此,引入i d,i q的前馈解耦控制,对e d,e q进行前馈补偿,且采用PI调节器作为电流内环控制器,则有方程

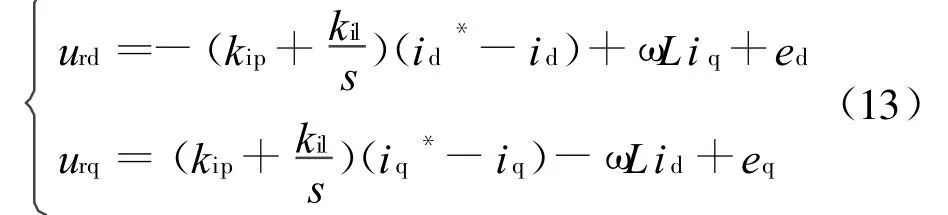
根据式(13)得整流器电流前馈解耦控制结构如图2所示。

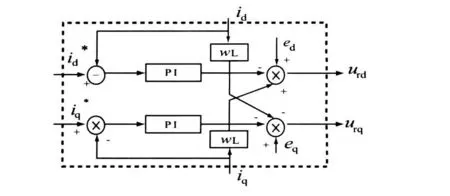
图2 电流前馈解耦控制结构图

3 本文所提方案控制原理图

系统控制框图如图3所示,与传统的直接电流控制系统不同之处在于本系统电压外环采用了滑模控制,具有滑模控制固有的响应快、鲁棒性强,抗扰性强等优点;另外采用固定开关频率的SVPWM技术对电流内环输出的控制信号进行调制,继承了SVPWM电压利用率高,动态响应快,容易数字实现的优点。具体SVPWM实施算法可参见文献[5],不再赘述。

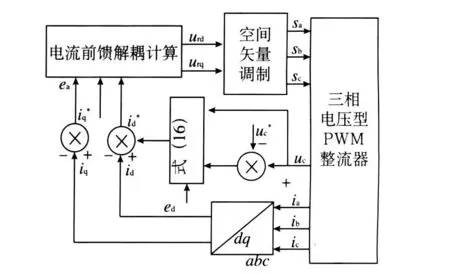
图3 系统控制原理图

4 系统仿真波形及分析

4.1 系统参数设置

为验证本文所提控制策略的可行性,利用Matlab对系统进行了数值仿真。系统仿真参数为：输入电源相电压幅值为311 V,输出直流电压u dc*=700 V,单位功率因数运行即i q=0,输入电感L=100 mH,线路等效阻抗为R=0.1Ω,直流侧电容为c=3 000μF,负载R=40Ω。开关频率 f=10 k Hz。控制系数参数为：μ=0.0015,k p=13,k i=50。

4.2 系统启动响应

图4分别为直流电压启动响应波形,电源输入a相电压和电流波形。从图4(a)可以看出直流电压响应速度快(0.01 s左右),无超调,无稳态误差;输入电流为正弦,电流总畸变率为2.99%,与电源电压相位一致,实现了单位功率因数的要求。

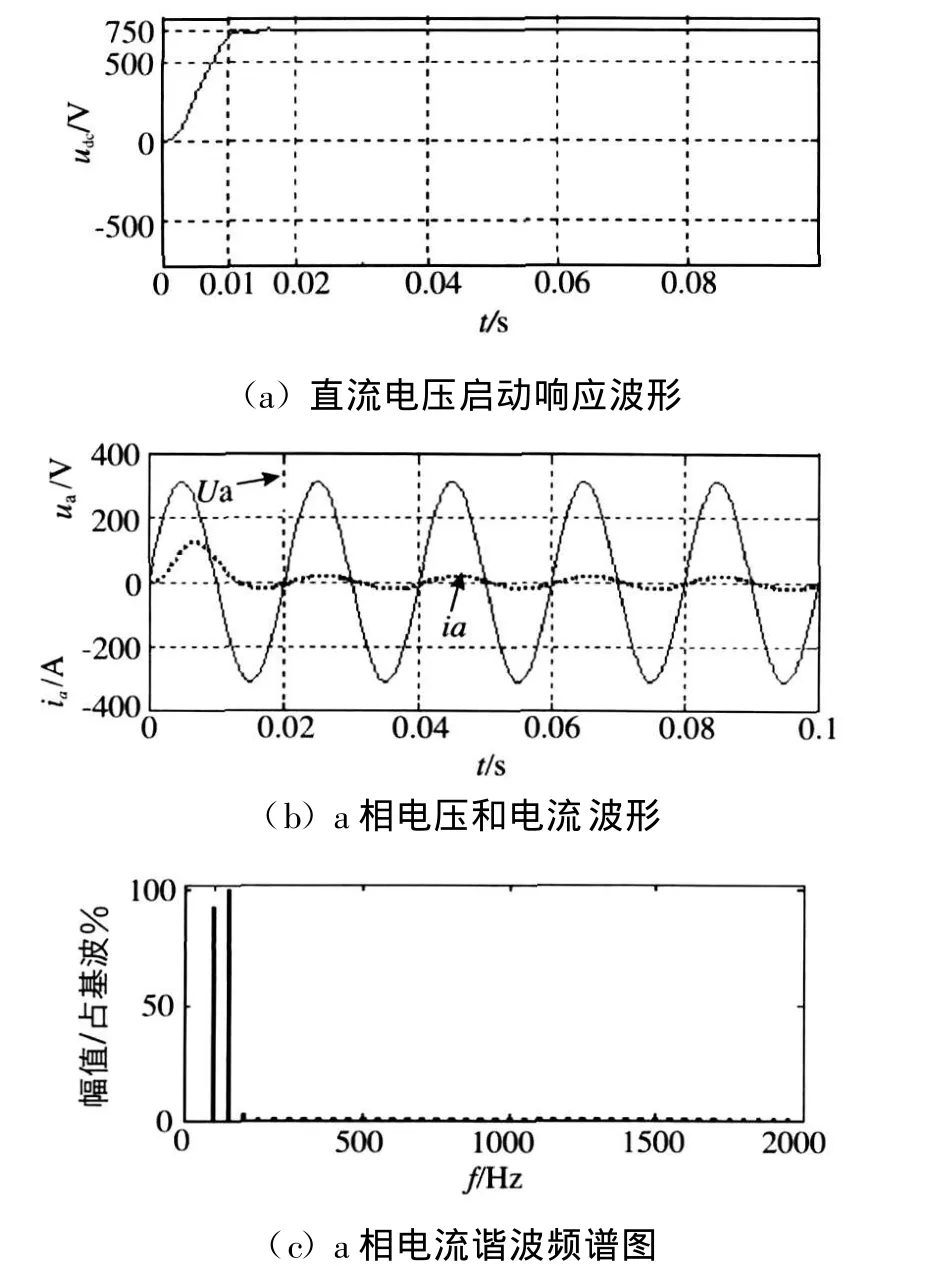
图4 系统启动响应波形

4.3 指令电压变化时系统动态响应

考虑输出电压指令值u dc*变化,周期性(0.1 s)由700 V调整到600 V,并且考虑负载在此时也发生突变,系统的动态响应波形如图5所示。可以看出直流侧电压较好地跟踪了指令输出值也即直流侧功率较好地跟踪了给定功率,其响应平滑,超调振荡几乎为0,鲁棒性强,响应在0.02 s左右。

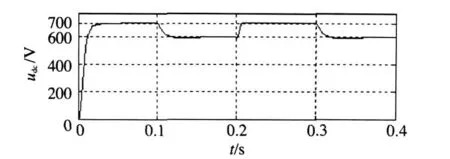
图5 直流电压响应波形

4.4 负载变化时系统的动态响应

考虑负载变化时,直流侧的电压响应情况。系统初始运行负载功率为12.25 k W,当系统运行在0.1 s时,突然把负载功率增到40 kW 运行,直到0.3 s,在0.3 s时负载功率减小到初始值一直运行,此过程系统的动态响应波形如图6所示。可以看出直流侧的电压随着负载的变化波动很小,无稳态误差,负载变动时系统恢复到稳定值的时间很短,在0.02 s左右。

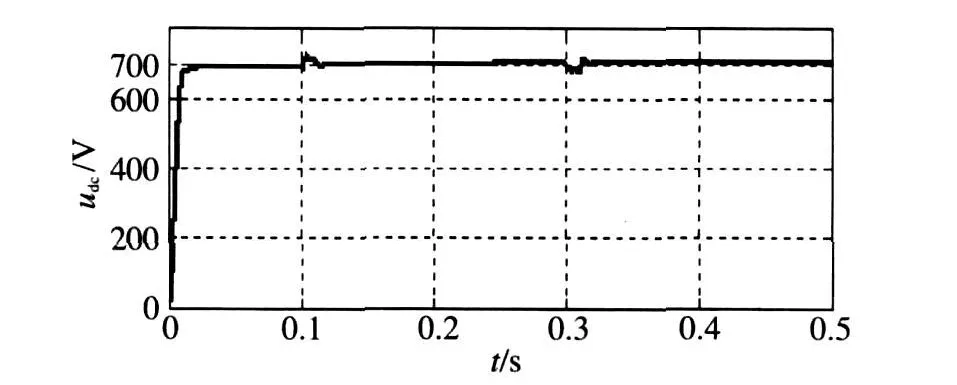
图6 负载变化时直流电压波形

5 结 论

根据电压型PWM整流器dq坐标系下的电流控制数学模型,提出了基于前馈解耦控制的电流内环、滑模控制的电压外环新控制策略。本系统采用了前馈解耦控制,实现了无功电流和有功电流的独立控制和单位功率因数;采用了滑模控制的电压外环,实现了直流电压的快速跟踪,增强了直流侧电压的稳定性和鲁棒性。新控制策略改善了传统直接电流控制的不足,具有系统响应快、稳定性好、抗负载扰动能力强等优点,计算机仿真证明了新控制策略的可行性和优越性。鉴于以上优点,本系统具有实际的开发研究价值。

[1] 张崇巍,张 兴.PWM 整流器及其控制[M].北京：机械工业版社,2003.

[2] 高为柄.变结构控制的理论及其设计方法[M].北京：科学出版社,1996.

[3] Lee T.Iuput-output linearization andzero-dynamics control of three-phaseac/dc voltage-sourceconverters[J].IEEE Transactions on Power Electronics,2003,18(1)：11-22.

[4] 张 强.基于的三相电压源型整流器系统设计[D].合肥：合肥工业大学,2003.

[5] 李 波,安群涛,孙兵成.空间矢量脉宽调制的仿真研究及其实现[J].电机与控制应用,2006,33(6)：40-44.

[6] 赵葵银.PWM整流器的模糊滑模变结构控[J].电工技术学报,2006,21(7)：49-53.