基于Newton法改进的BFGS迭代算法与Newton-CG算法

欧谦宁

（镇江高等职业技术学校，江苏镇江212016）

基于Newton法改进的BFGS迭代算法与Newton-CG算法

欧谦宁

（镇江高等职业技术学校，江苏镇江212016）

本文主要研究了数值分析中数值优化与非线性方程组求解这两个重要问题.文中首先概述了数值优化与非线性方程组的关系，然后对BFGS法的算法公式进行了改进，并对非线性方程组求解问题提出了一种改进的算法——Newton-CG算法.

数值分析；非线性方程组；Newton-CG算法

1 引言

建立合适的模型后，计算结果可能求不出来；但是我们可以根据目标函数和约束条件的特点，设计某种算法在计算机上给出一个近似的数值解.

一个好的算法应至少具备下面的标准.首先应该是一个收敛的算法，即该方法从某个合适的初始点启动，终止于问题的一个近似解；其次应该具有较快的收敛速度，这要求从迭代开始直到一个满足精度要求的近似解被找到的过程中，需要的迭代次数较少且每次迭代的运算量不大；最后，应具备较好的适用性，即解决同类问题中的大多数问题的能力.

数值优化和非线性方程组[1-3]的求解是数值分析的两个难点问题.本文介绍了改进的BFGS迭代算法，并且对非线性方程组的求解问题提出了一种新的算法——改进的Newton—CG算法.

2 数值优化与非线性方程组的关系

一般情况下fi=(x1,x2,…，xn)=0，i=(1,2,…,n)是非线性方程，于是无约束优化问题便可转化为求解非线性方程组方程组(1.1).

但是，文献[4]证明了非线性方程组问题通常是无法转化为无约束优化问题的.为此，本文的改进探讨意义重大.

3 改进的BFGS迭代算法

算法3.1(新BFGS法)

步1选取初始点x1∈Rn，初始矩阵B1酆0；

步2如果||塄f(xk)||<ε，迭代终止；

步3解方程Bkdk+塄f(xk)=0，得到一个新的下降方向dk；

步4利用黄金分割法确定步长αk；

步5计算新的迭代点xk+1=xk+αkdk，计算矩阵Ak，Bk+1；

步6令k+1←1，返回步1

可以证明：对于任何k，考虑由本算法生成的Bk,Ak，只要skTy*'k>0，则矩阵Vk+1一定正定.从而确保得到的dk一定是下降方向.并且可以证明此算法具有全局收敛性，通过此改进，使得拟Newton算法——BFGS更加有效.

4 非线性方程组的改进Newton-CG法

4.1 Newton法

n个变量n个方程的非线性方程组的一般形式为：

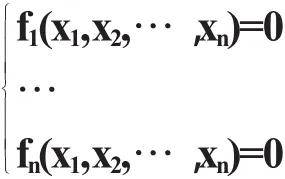
其中fi是定义在n维Euclid空间Rn中开域D上的实值函数.若用向量记号，令

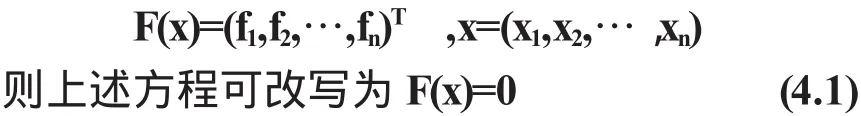
将非线性映像F：D奂Rn→Rn逐步线性化，在每个迭代中解一个线性方程组，这样的迭代法称为线性化方法.对方程(4.1)可构造线性方程组Lk(x)=Ak(x-xk)+F(xk)=0，其解为xk+1，并可以作为方程(1.1)的新近似，即xk+1=xk-Ak-1F(xk),k=0,1,…

通常Ak与xk及F，F'等有关，文献[3]指出Ak的取法不同对应着不同的方法

当Ak=F'(x0)，xk+1=xk-[F'(x0)]-1F(xk)，称为简化Newton法；kk+1kk-1k

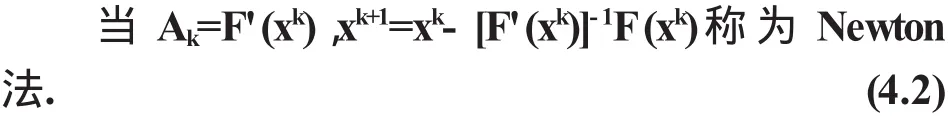
Newton法(4.2)式当n很大时计算比较困难，常采用下面形式

这样每步解一个n阶线性方程组，称(4.3)为Newton方程组，并且可以证明Newton法是局部二阶收敛的.

算法4.1(Newton法)[3]

步1给出初始近似x0及其计算精度ε1,ε2；

步2假定已进行了k次迭代，已求出xk及F (xk)，计算Ak=F'(xk)；

步3解线性方程组F'(xk)△xk+F(xk)=0，得到△xk；

步4求xk+1=xk+△xk及F(xk+1)；

步5若||xk+1-xk||≤ε1或||F(xk+1)||≤ε2，x*=xk+1；否则，k+1→k，转步2；

从上面算法可以看出，Newton法具有收敛快，自校正的优点；它的缺点是(1)局部收敛，要求初试近似x0与x*充分靠近；(2)当n较大时，每步都计算Jacobi阵，工作量大；(3)解(4.3)线性方程组时，F' (xk)可能非奇异或者病态.

4.2 改进的Newton-CG法

用Newton法求解Newton方程组时，常用的方法是Newton-SOR迭代法和非线性SOR-N方法.本文提出一种改进的Newton法，即方程组F'(xk)△xk+F (xk)=0是关于△xk的线性方程组，当F'(xk)对称正定时，可以用共轭梯度法求此方程，但一般情况下F' (xk)不能达到如此高的要求，故必须对Newton方程组改进,对(4.3)式两边同时做矩阵乘法运算，即得到新的Newton方程：

记A=(F'(xk))TF'(xk)·b=-(F'(xk))TF(xk)，可以证明A是对称正定矩阵，故满足共轭梯度法的条件，可以使用共轭梯度法，避免求逆运算，提高算法的有效性.

算法4.2(改进的Newton-CG法)

步1给出初始近似x0及其计算精度ε1,ε2；

步2假定已进行了k次迭代，已求出xk及F (xk)，计算Ak=F'(xk)；

步3对线性方程组F'(xk)△xk+F(xk)=0变形，得到新的Newton方程(F'(xk))TF'(xk)△xk+(F'(xk))TF(xk)=0，用共轭梯度法得到△xk；

步4求xk+1=xk+△xk及F(xk+1)；

步5若||xk+1-xk||≤ε1||xk||或||F(xk+1)||≤ε2，x*=xk+1；否则，k+1→k，转步2.

可以证明，改进的Newton-CG法总体上仍然具有Newton法的二阶敛速，每步迭代计算2n个分量函数值和n2个函数乘法，但避免了矩阵求逆，计算量相对减少，存储空间也随之减少，与N—SOR法相比，不需要进行矩阵分解，因此很大程度上提高了算法的有效性.

〔1〕冯果枕.非线性方程组迭代解法[M].上海:上海科学技术出版社,1986.

〔2〕晁玉翠.求解非线性方程组的修正牛顿法研究[D].哈尔滨:哈尔滨工业大学,2007.

〔3〕李庆扬,莫孜中,祈力群.非线性方程组的数值解法[M].北京:科学出版社,1987.

〔4〕王德人.非线性方程组解法与最优化方法[M].北京:人民教育出版社,1979.

〔5〕Z Wei,G Li,L Qi.Newton quasi-Newton method for unconstrained optimization problem [J],AppliedMathematicsandComputation, 2006,175:1156-1188

〔6〕Y Dai.Convergence properities of the BFGS algorithm[J].SIMA journal on optimization, 2003,13:693-701.

O29

A

1673-260X（2010）11-0006-02