利用向量方法探求“线性回归方程”新路,并用“Scilab”新工具验证
2010-09-21苏艳华史秀英
苏艳华,史秀英
(1.沈阳大学理学院,辽宁沈阳110044;2.赤峰学院继续教育部,内蒙古赤峰024000)
利用向量方法探求“线性回归方程”新路,并用“Scilab”新工具验证
苏艳华1,史秀英2
(1.沈阳大学理学院,辽宁沈阳110044;2.赤峰学院继续教育部,内蒙古赤峰024000)
本文把高中课本中向量的有关概念作了推广,利用向量方法探求“线性回归方程”新路,并用“Scilab”新工具验证.
向量方法;线性回归方程;Scilab
本文推广了高中课本中向量有关概念,然后利用向量方法探求“线性回归方程”新路,并用“Scilab”新工具给予验证.
1 向量有关概念的推广
在平面解析几何中,两个点A和B间的距离等于以点O为起点的两个向量O!"A,O!"B的端点之间的距离,这个长度就是两个向量O!"A,O!"B的差O!"A-O!"B的模,它也可以理解为两个向量O!"A,O!"B的距离.那么在空间两个向量的距离不妨也可以类似定义:
定义1设α与β是空间任意两个向量,|α-β|称为向量α和β的距离,记为d(α,β).
在平面向量中我们学过平行(共线)向量的概念,对于空间向量,不难理解任何两个向量都是共面的,共面向量我们不妨这样定义:
定义2在空间中存在一个向量β若与一个向量集合W中的每一个向量都垂直,则称向量集合W中的向量共面.
定义3上面集合W中的每一个向量经过平移后都能平移到某一个平面α中,平面α与向量集合W的并集称为向量平面L,在满足定义2的条件下,称向量β垂直于向量平面.
在立体几何中,平面外一点到平面内一点的距离,连接两点的线段与该平面垂直时距离最短,由此不难想到:
结论在空间向量中的一个向量β到一个向量平面L中一向量α的距离,当向量α-β与向量平面L垂直时最短.
先设向量平面为L,它是由若干向量α1,α2,…,αk所生成,表示为
L(α1,α2,…,αk),设α是L中的向量,如图1.
分析可知:若向量α-β垂直于向量α,则有|α-β|≤|αi-β|.
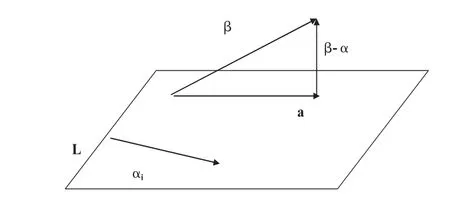
图1
在人教版B版第二册教材“阅读材料”第51页“向量概念的推广”中,将向量空间扩充到了n维,因此猜想有以下结论成立.
结论1在n维空间中上面的三个定义仍然成立,且在n维空间中两个向量垂直,则有这两个向量的数量积为0.
结论2在n维空间中的一个向量β到一个向量平面L中一向量α的距离,当向量α-β与该向量平面L垂直时最短.
2探求“线性回归方程”新路
下面分析人教版第一章第六节“线性回归”中的例题:一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万元)之间有如下一组数据(如表1):

表1
(1)画出散点图(2)求月总成本与月产量之间的回归方程.
通过图形分析可以看出两个数量关系接近直线关系,下面用向量的方法求解
解:设求出的方程为y=bx+a,即a+bx-y=0
列出表2:
i由此根据以上给出的数据可以构造以下方程组
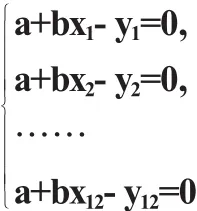
下面求a,b使最小即可.

表2

由以上的猜想,构造向量β=(y1,y2,y3,……,y12),可以设一个向量集合W,构造向量α=(a+bx1,a+bx2,a+bx3,……a+bx12)∈W.
向量集W中的向量是否共面,还不知道,若不共面就不能用以上的结论处理,在这里可以先做一个假设,设W中的向量共面,它们的向量平面为L,这样要使(1)式最小只要使|β-α|2取最小值即可,即在共面向量W中找一个向量α0=(a0+b0x1,a0b0x2,……,a0b0x12),使得向量β-α0与平面向量L中的任何一个向量都垂直,即(β-α0)·W=0.

所以每月的总成本与该月产量的关系近似方程可为: 0.9583+1.2283x-y=0,在这里因为找到了一个向量与向量空间W中的任何向量都垂直,也间接证明了向量集合W共面.
3 “Scilab”新工具验证
Scilab是一个科学计算软件,它主要有两个功能:数值计算和计算结果可视化.在高中数学人教新教材B版的教材中,在算法的学习与算法思想的渗透等很多方面使用Scilab来体现.下面就上面的问题在“Scilab”环境下通过算法的思想给予验证.
根据给出的数据可以在“Scilab”的“编辑”视窗下编写以下的程序:
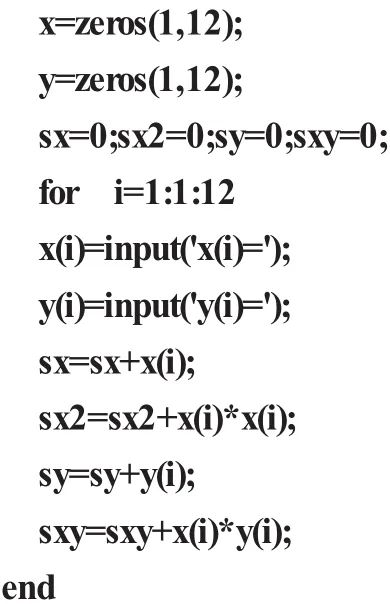
而后再到主窗口下运行(将以上程序复制到主窗口):并输入输入以下数据(x,

x1.081.121.191.281.361.481.591.681.801.871.982.07 y2.252.372.402.552.642.752.923.033.143.263.363.50


〔1〕人民教育出版社课程教材研究所中学数学课程教材研究开发中心.普通高中课程标准实验教科书数学2(必修B版).人民教育出版社,2007.
〔2〕人民教育出版社课程教材研究所中学数学课程教材研究开发中心.普通高中课程标准实验教科书数学2(选修Ⅱ).人民教育出版社,2007.
〔3〕马现岭.让scilab走进高中数学教学.人教网,2009-2-27.
O151
A
1673-260X(2010)11-0008-02
