三阶KdV方程一般形式的精确解

郝艳花

(山西大同大学数学与计算机科学学院，山西大同037009)

三阶KdV方程一般形式的精确解

郝艳花

(山西大同大学数学与计算机科学学院，山西大同037009)

对求解非线性数学物理方程的F-展开法进行了扩展，并利用齐次平衡原则求出KdV方程的椭圆函数表示的精确解，在极限情形下，得到该方程的三角函数表示的周期波解.

KdV方程 F-展开法 齐次平衡原则 精确解

非线性数学物理方程的精确解在非线性问题中占有重要的地位，现在已有诸多求非线性数学物理方程精确解的新方法，例如齐次平衡方法，F-展开法，Jacobi椭圆函数展开法等等.本文利用F-展开法，结合齐次平衡原则求得了KdV方程一般形式的精确解.本方法可以用来求解其他的非线性数学物理方程.

1 方法简介

考察非线性偏微分方程

其中等式左端为u及其各阶导数的多项式.

利用F-展开法求解方程(1)的步骤如下：

1)先求方程(1)的行波解，即令

其中c为波速.将(2)式代入方程(1)，则方程(1)可化为常微分方程

设u(ξ)可表示为F(ξ)的有限幂级数

其中a-N,…,aN为待定常数,F(ξ)满足方程

这里P,Q,R为待定常数，正整数N由具有支配地位的非线性项与最高阶导数项齐次平衡确定.

2)将(4)式代入方程(3)，再利用(5)式，即可将方程(3)的左端化简为F(ξ)的多项式.再令F(ξ)的各次幂项的系数为零，即可得到关于a-N,…,aN和c的代数多项式.

3)解上述方程组 (可借助 Mathematica或Maple)，可求得由P,Q,R表示的a-N,…,aN和c，将在线结果代入(4)式，即可得方程(1)的行波浓缩公式.

4)给P,Q,R赋值，使方程(5)的解F(ξ)是Jacobi椭圆函数，代入方程(1)的行波浓缩公式，在极限情形下，得到该方程的三角函数表示的周期波解.

2 KdV方程一般形式的行波浓缩公式

考虑KdV方程

将(2)式代入方程(6)得

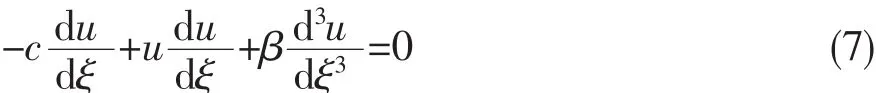
方程(7)两边对ξ积分，并取积分常数为零，得

设方程(7)的解具有

的形式.其中a-N,…,aN为待定常数.

由(8)式可知

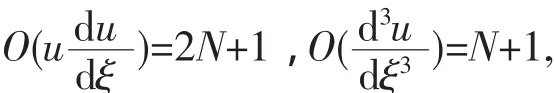
再由u″与u2齐次平衡可确定正整数N=2.故设方程(7)的解为:

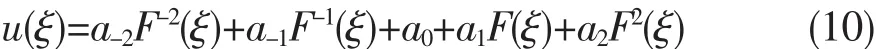
其中a2≠0，F(ξ)满足方程

易求的

将(10)式代入到方程(8)，并利用方程(11)(12)，可将方程(7)的左端变为F(ξ)的多项式

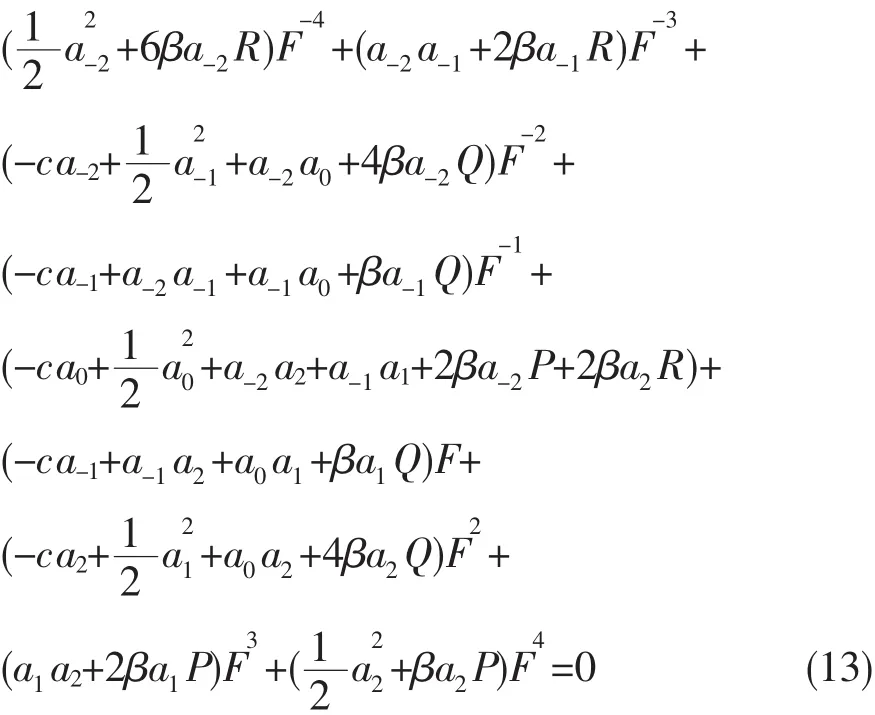
令(13)式中的各次幂的系数为0，则可得到关于a-2, a-1,a0,a1,a2的代数方程组，令求的其解有以下4种情况：

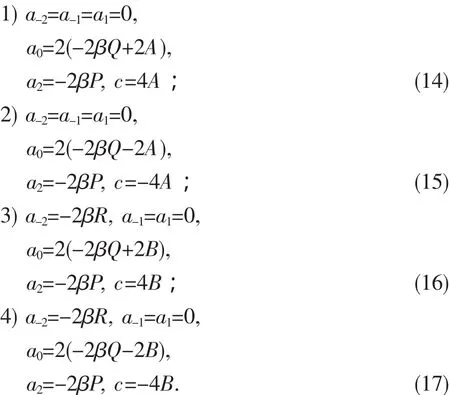
将以上4组解(14)-(17)代入到(10)式中，即可得到方程(6)四个行波浓缩公式：

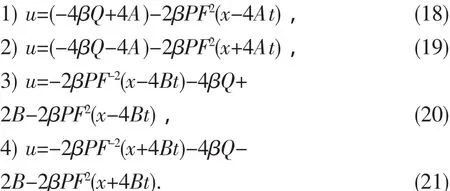
3 KdV方程的周期波解

选取适当的P,Q,R，利用P,Q,R与F的对应关系，m为模，记

由式(18)-(21)即可得到KdV方程的周期波解：

1)取P=m2,Q=-(1+m2),R=1则F=snξ，F=cdξ,得周期波解有：

2)取P=1,Q=-(1+m2),R=m2则F=nsξ，F=cdξ,得周期波解有：

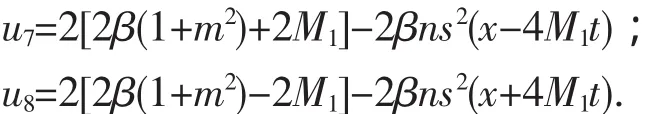
3)取P=m2-1,Q=2-m2,R=-1,则F=ndξ,得周期波解有：

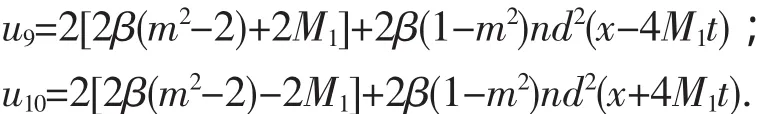
4)取P=1-m2,Q=2m2-1,R=-m2,则F=ndξ,得周期波解有：

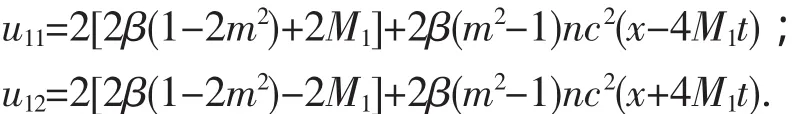
5)取P=-m2,Q=2m2-1,R=1-m2,则得周期波解有：

6)取P=-1,Q=2-m2,R=m2,则F=dnξ,得周期波解有：

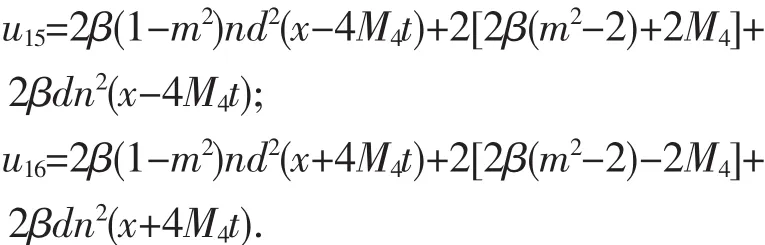
7)取P=1-m2,Q=2-m2,R=1,则F=scξ,得周期波解有：

8)取P=-m2(2-m2),Q=2m2-1,R=1,则F=sdξ,得周期波解有：

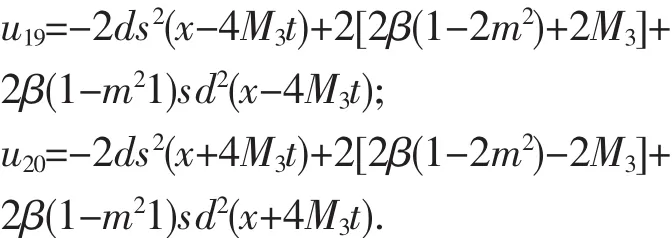
4 三角函数表示的周期波解

1)当m→0时，得到方程(6)的三角函数表示的周期波解有：

2)当m→1时，得到方程(6)的三角函数表示的周期波解有：

综上所述，本文将F-展开法变化到正负幂的形式，不仅丰富了F-展开法，而且求得了KdV方程的精确解，尤其是用两个Jacobi椭圆函数表示的精确解，该方法还可以用来求解一大类数学物理方程.

[1]Wang Mingliang.Exact Solution for a Compound KdV-Burgers Equation[J].Phys Lett A，1996,213:279-287.

[2]张金良，李向正，王明亮.变系数Burgers方程的一些新的精确解[J].河南科技大学学报：自然科学版，2004，25(1)：86-89.

[3]刘式适,傅遵涛,刘式达,等.Jacobi椭圆函数展开法及其在求解非线性波动方程中的应用[J].物理学报，2001，50(11)：2068-2073.

[4]李向正，王跃明，李晓燕，等.组合KdV-Burgers方程的一种解法[J].河南科技大学学报：自然科学版，2003，24(4)：104-107.

[5]付遵涛，刘式适，刘式达.非波动方程求解的新方法[J].物理学报，2004,53(2):343-348.

[6]李向正，闫杰生.KdV方程的一种新解法[J].河南科技大学学报：自然科学版，2005，26(3)：73-75.

[7]李保安，李向正，罗娜，等.n维Klein-Gorden方程的一种解法[J].河南科技大学学报：自然科学版，2004，25(1)：82-85.

[8]李保安，李修勇，李晓燕，等.变形Boussibesq方程组的周期波解和孤立波解[J].河南科技大学学报：自然科学版，2004，25(2)：91-94.

Abstract:The F-expansion method is extended on solving nonlinear mathematical physics equations,and exact solutions of KdV equation expressed elliptic functions are obtained by using the homogeneous balance principle.In the limit cases,the equation of the trigonometric functions are expressed in periodic wave solutions.

Key words:KdV equation;F-expansion method;homogeneous balance principle;exact solutions

〔编辑 高海〕

Exact Solutions to Third-order KdV General Form Equation

HAO Yan-hua
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)

O13

A

1674-0874(2010)05-0010-03

2010-06-06

郝艳花(1973-)，女，山西广灵人，硕士，讲师，研究方向：计算数学.