一类二阶微分方程最终正解的单调性
2010-09-20陈慧琴赵香兰
陈慧琴,赵香兰
(山西大同大学数学与计算机科学学院,山西大同037009)
一类二阶微分方程最终正解的单调性
陈慧琴,赵香兰
(山西大同大学数学与计算机科学学院,山西大同037009)
研究了一类二阶非线性微分方程(a(t)x′)′+P(t,x)=Q(t,x,x′)最终正解的单调性,给出了判断其最终正解单调的充分条件,并用例说明了主要结论.
二阶非线性微分方程 最终正解 单调性
近几年,许多专家学者研究了微分方程的渐近性、振动性及其应用,如文献 [1-5],在此影响下,本文研究了二阶非线性微分方程
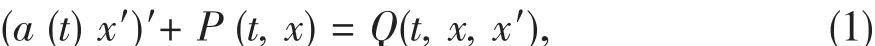
其中a(t)∶[t0,∞)→R,a(t)>0,P∶[t0,∞)×R→R,Q∶[t0,∞)×R2→R,Q为连续函数.文[1]研究的是方程(1)的振动性,而本文给出了判别方程(1)最终正解具有单调性的充分条件.为此,设存在连续函数f∶R→R满足:
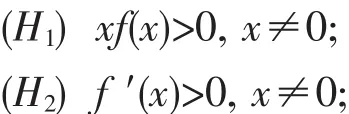
(H3)存在两个函数p(t),q(t),使得
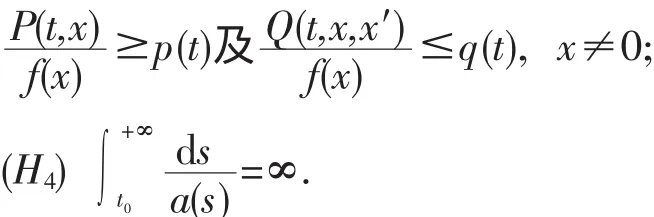
下面我们给出主要定理,并用例题说明.
定理1设(H1)—(H4)成立,且

对所有t0成立,则方程(1)的最终正解是最终单增的.
证明 设x(t)为方程(1)的最终正解,即存在T,当t>T>t0时,x(t)>0.如果结论不成立,不失一般性,可设x′(T)≤0,由方程(1)及条件得对(2)式积分,得
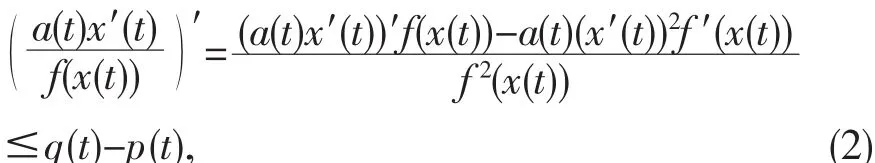
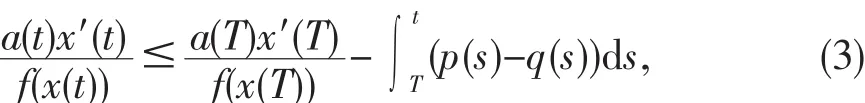
由条件可知,当t≥T时,x′(t)<0.由方程(1)积分并利用条件(H3),有
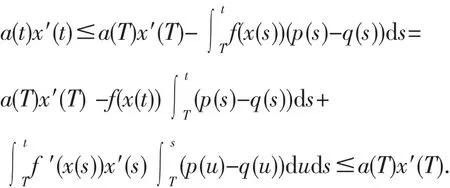
两边同时除以a(t)并积分,有
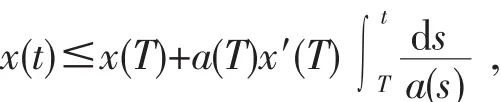
由(H4)知,当t→∞时,x(t)→-∞,这与x(t)>0矛盾.
例1考虑方程
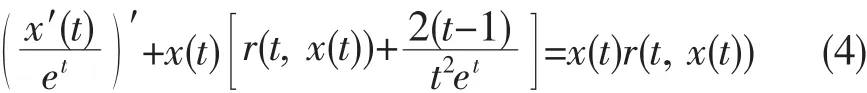
这里r(t,x)为任意的函数,取f(x)=x,则

定理2 若 (H1)-(H4)成立,且存在T>0,t1≥T,使得对每一个t0≥0,使得则方程(1)最终正解x(t)最终单增或满足
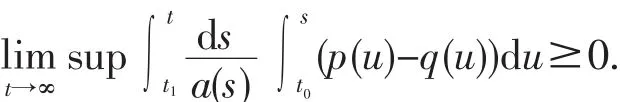
证明设x(t)为方程(1)的最终正解,即存在T,当t>T>t0时,x(t)>0.如果结论不成立,不失一般性,可设x′(T)≤0,且
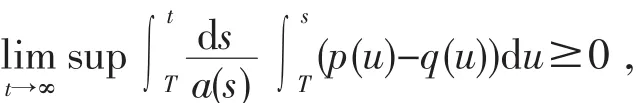

对上式积分,可得
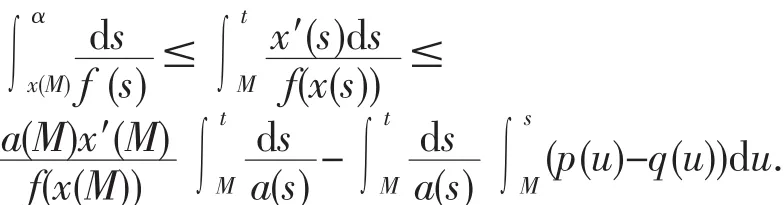
由条件可知矛盾.
例2考虑方程
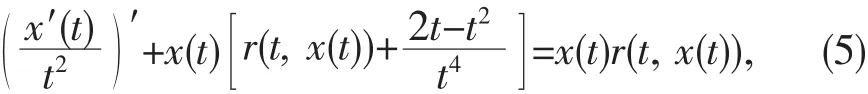
这里r(t,x)为任意的函数,取f(x)=x,则
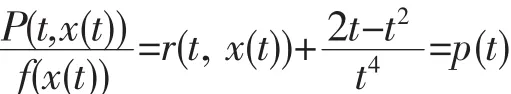
及
Q(t,x,x′)=r(t,x(t))=q(t),
f(x(t))
定理3设(H1)-(H3)成立,且
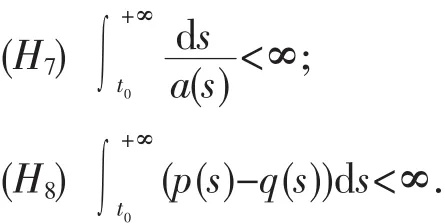
对所有t0成立,则方程(1)的最终正解是最终单减的.
证明假设结论不成立,不妨设x(t)为方程(1)的最终正解,即存在T,当t>T>t0时,x(t)>0,而且x′(t) >0,x′(T)>0.则由(3)得
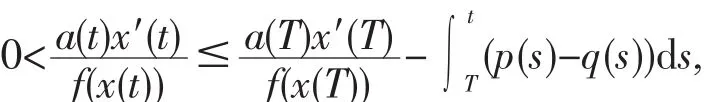
即有
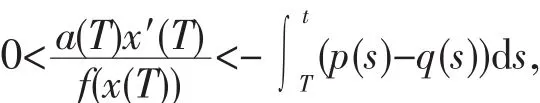
这是一个矛盾式.
例3考虑方程

这里r(t,x)为任意的函数,取f(x)=x,则

所以p(t)-q(t)=et(2t-1-6t-2),而a(t)=et,则方程(6)满足定理3的条件,所以方程(6)有一个单减正解
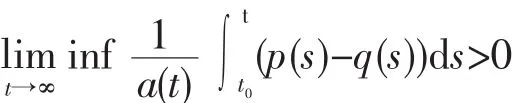
对所有t0成立,则方程(1)的最终正解x(t)或最终单增或最终单减且满足
定理4若(H1)-(H3)成立,且
证明 设x(t)为方程(1)的最终正解,即存在T>t0,当t>T>t0时,有x(t)>0.如果结论不成立,不失一般性,可设x′(T)≤0,且
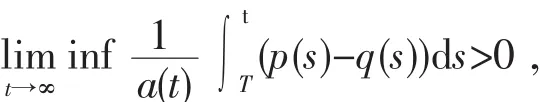
则存在实数β>0,使得

由(3)式,得

所以

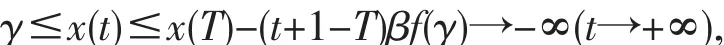
这是个矛盾式.
[1]Zhang G,Cheng S S.Existence of solutions for a nonlinear system with a parameter[J].J Math Anal Appl,2006,314(1):311-319.
[2]Zhang G,Yan J R.Solutions On an Impulsive compartmental system,Dynamics of Continuous,Discrete and Impulsive Systems, Series A,2009,16:725-735.
[3]崔亚琼,宋海竟.二阶微分方程解的存在唯一性及解得性质[J].山西大同大学学报:自然科学版,2009,25(5):24-25.
[4]张英.时间模上二阶3-点边值问题的两个正解[J].山西大同大学学报:自然科学版,2008,24(6):1-4.
[5]张广,高英.差分方程的振动理论[M].北京:高等教育出版社,2001.
[6]Grakf J R,Rankin S M,Spikes P W.Oscillation theorems for perturbed nonlinear differential equations[J].J Math Appl,1978,65: 375-390.
Abstract:In this paper,we derive several sufficient conditions for monotonicity of eventually positive solutions on a class of second order nonlinear differential equation(a(t)x′)′+P(t,x)=Q(t,x,x′).We also provide example to illustrate our main results.
Key words:second order nonlinear differential equation;eventually positive solution;monotonicity
〔编辑 高海〕
Motnotonicity of Eventually Postive Solutions on a Class of Secord Order Nonlinear Diffevential Equation
CHEN Hui-qin,ZHAO Xiang-lan
(School of Mathematics and Computer Sciences,Shanxi Datong Universty,Datong Shanxi,037008)
O177
A
1674-0874(2010)05-0003-02
2010-04-20
陈慧琴(1964-),女,山西大同人,副教授,研究方向:差分方程.
