最优路径查询的研究与实现
2010-09-20周志富
杨 莉,周志富
(山西大同大学工学院,山西大同037003)
最优路径查询的研究与实现
杨 莉,周志富
(山西大同大学工学院,山西大同037003)
车辆导航正成为现代交通的一种服务趋势,而其中重要的、必不可少的一部分就是最优路径的查询.对最优路径查询的原理、数据组织、数据结构和查询算法进行了研究,然后利用实验数据,实现了最优路径查询功能,证实了实现最优路径查询的方法是有效的.
最优路径查询 ARC-NODE结构 启发式算法
随着城市道路系统日益增加及复杂,自驾车的数量和困难也随之增加,车辆导航成为一种重要的服务手段,因而导航地图日渐成为现代交通中的一个重要部分,而其中最优路径查询功能又是其核心,因此,研究最优路径查询的实现对于车辆导航具有重要的现实意义,同时该产业也具有巨大的经济前景.
目前,国外在导航方面做得已经比较成熟,相比之下,我国还有一定的差距,不论是数据库建立还是实际应用研究都还不够,市场上的专门公司也较少,产品仅处于推广阶段.
1 最优路径查询原理
最优路径查询,如距离最短或时间最短或费用最低的路径查询是车载导航系统中常见的一种查询方式.一般是通过输入目的地而得到想要的最优路线,车辆在导航系统的辅助下,能够尽快到达目的地.该查询最终落实到对地图数据库的检索,即根据给定条件确定相应地物集合的数据库逻辑地址.对于最优路径查询来说主要就是对道路信息数据的检索,车辆在行进中,借助GPS卫星提供的定位数据,将车辆现在的位置反映到导航地图中,一旦指定了目的地后,系统在后台进行包含这两个特殊位置的图搜索,即将复杂的道路网转换为数学意义上的图,这样就可借助图搜索算法找到一条满足用户要求的最优路径,车辆借助卫星导航系统和惯性导航仪就可以较快地到达目的地.其中搜索数据库的过程中需要将结果的数据库坐标转化为用户坐标,提交给用户[1].该过程涉及到坐标系统的转换,图搜索算法的高效运行和地图匹配等问题,但核心是图搜索算法的高效运行.
2 数据的组织
在美国,NavTech为许多主要城市区域提供可用的导航数据库.数据库中的信息包括道路网几何形状、道路等级、道路特征 (如方向性)、转弯和限制、制图和地理政治边界、感兴趣的点、路标和服务设施[2].这对我们建立最优路径查询用的数据库具有很好的参考价值.
数据结构方面,ARC-NODE结构能表示完整的矢量弧段-结点拓扑关系,每个地物用一个编码标识置于选定的位置,地物的属性存储于关系表中,它非常适合路网的表示,我们可以将路网抽象为点和线组成的网,将一条路分割为几段,每段表示为一条线,线间接点及道路交叉口可用点表示,而这些点和线的属性信息可以存储在关系表中,反映连通性和方向性,这样即储存了主要的交通信息,又表示出了路段间的拓扑关系,将复杂的道路网表示成数学意义上的一个图,该图可以是有向的,还可以是被赋权的,从而作为车辆导航系统核心技术确定某两地间的最优行驶路线问题便可以转化为在赋权图上求两点间的最短路径问题[3].
3 最优路径查询算法
传统Dijstra[4]算法是一种按路径长度递增的顺序产生最短路径的方法,是寻找最短路径的传统方法.它把所有结点分成两组,OPEN表存储已经产生但还没扩展的结点,CLOSED表存储已经扩展的结点 (最短路径点),按最短路径长度递增的顺序,逐个把OPEN表的结点加到CLOSED表中,直到从图中第一个结点出发可以到达的所有结点都已经包括在CLOSED表中,在该过程中,总保持从第一个结点到CLOSED表各结点的最短路径都不大于从第一个结点到OPEN表的任何结点的最短路径长度.此外,每个结点对应一个距离值,CLOSED表的结点对应的距离就是从第一个结点到此结点的只包括CLOSED表的结点为中间结点的最短路径长度,OPEN表的结点对应的距离值是从第一个结点到此结点的只包括CLOSED表的结点为中间结点的最短路径长度.该算法能得到最短路径的最优解,但由于它遍历的结点很多,所以效率低.不能满足导航快速反馈的要求,一种解决方法是采用启发式算法A*提高其效率,即提供一个结点距离目标点有多远的估计,以使搜索算法优先考虑最有希望的结点.对每个结点定义一个估价函数,A*[5]算法优先搜索具有最小估价函数值的结点,每个结点的估价函数值为从原点到当前结点的实际距离与当前结点到目标结点的最短距离之和.
实际中最优路径还可以是时间最短或费用最低的路径,操作起来和搜索距离最短路径是原理一样,只是各个结点上的距离变成时间或费用.
4 实验
获取某市矢量地图,确保投影为经纬度投影,坐标系为WGS84的,符合车载电子地图服务系统的要求.保留河流、建筑物、绿地等基础信息图层.下面按照前面介绍的数据组织策略存储数据.
为满足路径信息的查询,采用ARC-NODE结构建立了道路信息数据库,存储内容为:道路类型(首级道路标记为1,次级道路标记为2)、道路名称、路段的起始点标记、路段的长度、路段起止点的标志、估计的行车时间 (利用路程除以平均速度得到)这些信息.道路信息表存储道路图层中各个路段结点的坐标和代码.具体如表1、表2所示.
对组织好的数据,应用前面介绍的A*算法,实现了小范围内的距离最短和时间最短的最优路径查询,结果如图1、图2所示.图1中指定起始位置和目的地后,给出最短行车距离为4.79km的路线为:保健街-求真路-建设路-兴胜街-前进路-爱国街-中华路-人民大街-八一路-工业街-东风路-东环路.图2中指定起始位置和目的地后,给出估计的行车时间为5.73 min,具体路线为:保健街-求真路-兴胜街-前进路-常青街.
对于大范围、大数据量的最优路径查询时,对数据的组织还会应用到分尺度、分区域、地图分幅组织及索引等策略,并注意到地图匹配等问题,鉴于本文的实验数据量小、范围小,因此没有进行这些方面的研究.
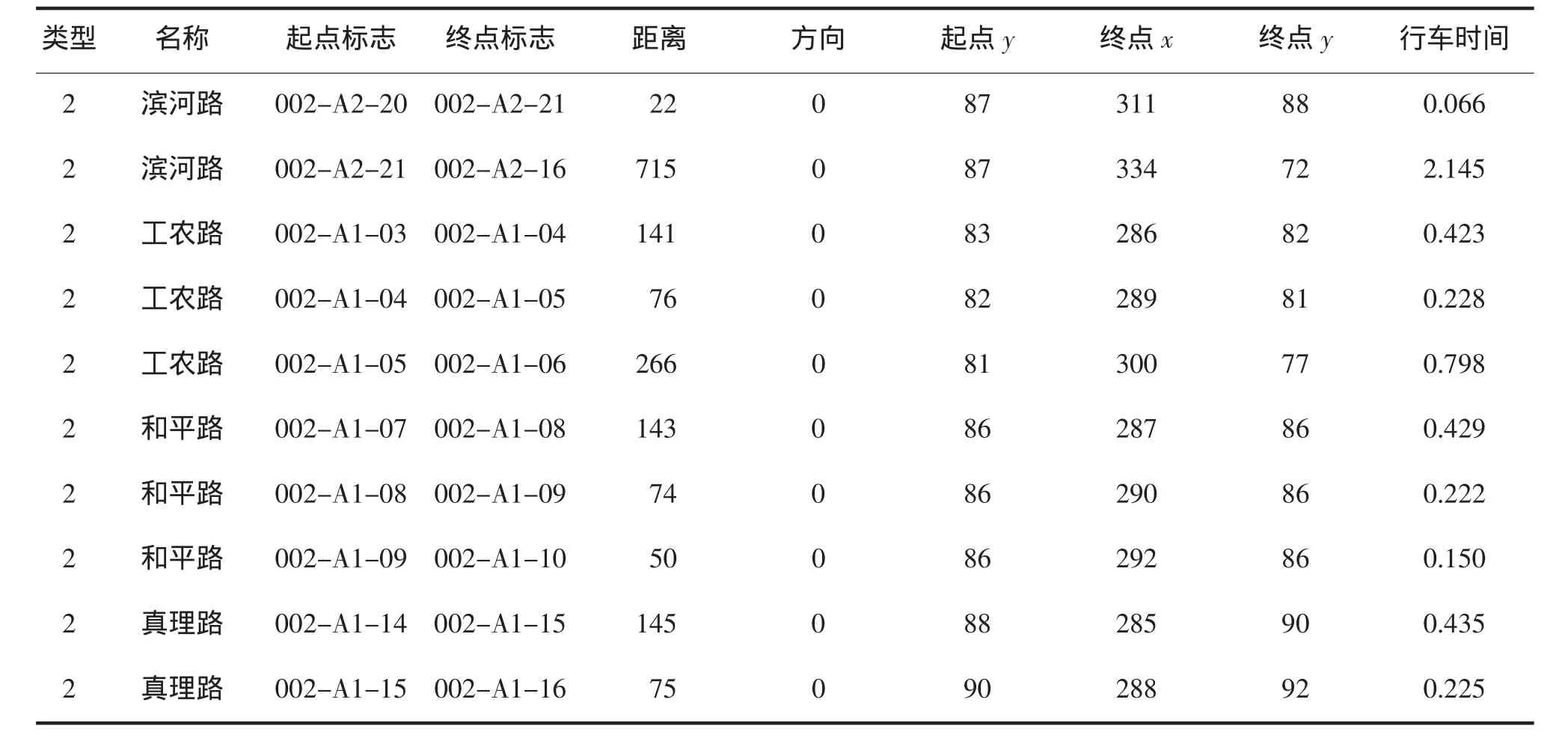
表1 道路关系表
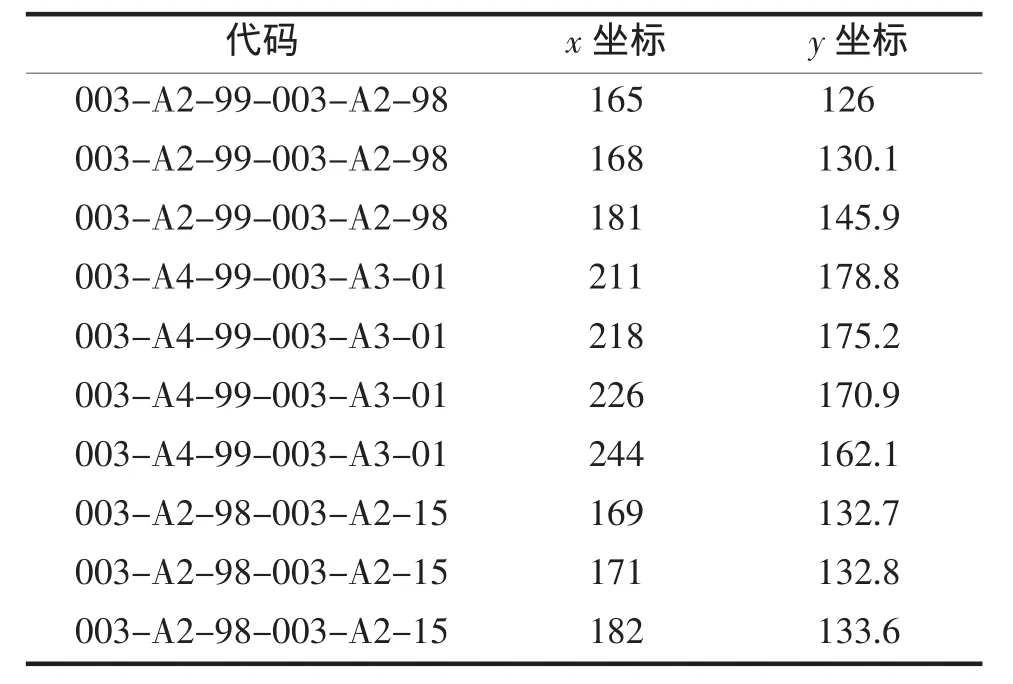
表2 道路信息表
5 结论
本文针对导航服务中的最优路径查询功能,进行了一系列理论研究,后采用ARC-NODE结构、对实验数据进行了合理的分层和组织及处理,采用启发式Dijstra算法或A*算法,最终实现了小范围内的最优路径查询功能.大范围、大数据量的最优路径查询还有许多问题有待进一步研究.
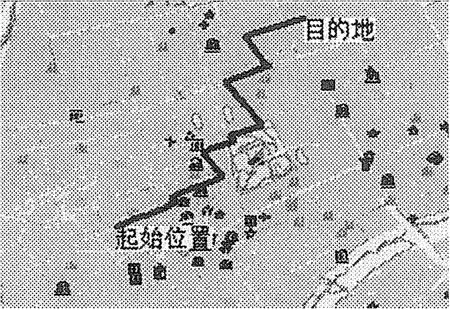
图1 距离最短路径查询

图2 时间最短路径查询
[1]毋河海.地图数据库系统[M].北京:测绘出版社,1991.
[2]蒋捷,韩刚,陈军.导航地理数据库[M].北京:科学出版社,2003.
[3]杨长保,于银辉.基于VC++的ARC/INFO集成二次开发[J].吉林大学学报:科学信息版,2003,21(2):162-166.
[4]唐策善,立龙澎,黄刘生.数据结构-用C语言描述[M].北京:高等教育出版社,2002.
[5]LEE TIAN SZE,TAN KAR ENG.Vehicle navigation and route guidance[D].Nan yang Technological University:School of electrical and electronic engineering,2002.
Abstract:Vehical navigation is becoming a serving trend in modern traffic and the important and the necessary part is the optimal rout query.It did some research on the principle of the optimal rout query,data organization,data structure and query algorithm. Then it realizes the optimal rout query using the experimental data.The result confirms the effectiveness of the method of the optimal rout query realized in the paper.
Key words:The Optimal Rout Query;ARC-NODE structure;Heuristics Algorithm
〔编辑 高海〕
Research and Realization of the Optimal Route Query
YANG Li,ZHOU Zhi-fu
(School of Engineering,Shanxi Datong University,Datong Shanxi,037003)
P28
A
1674-0874(2010)05-0023-03
2010-04-20
杨莉(1983-),女,河北安国人,硕士,助教,研究方向:地理信息系统.
