关于正态分布,偏态分布的等距分组
2010-09-20贾振声
贾振声
(重庆三峡学院经管学院,重庆万州404000)
关于正态分布,偏态分布的等距分组
贾振声
(重庆三峡学院经管学院,重庆万州404000)
一组数据进行等距分组,到底分多少组?为此我们对正态分布进行研究,通过公式得出了计算分组的算法.
均值 方差 拟合函数 全距 四分之一距
各种统计方面的书,在讨论等距分组的时候,对经验公式或者只把它当作参考,或者干脆不用.原因是经验公式,组距只与数据个数有关,而与数据拟合的函数形状无关.
对服从正态分布的数列,我们进行了研究,得出求组距的方法,这个方法简单适用.其次,推出的公式对偏态分布也适用.
1 直方图及组距的上界
1.1 直方图
(1)观测量x1,x2,…,xN;找出其最小值x*1和最大值
R为全距.一般的l≥2,即分组,分5个组或5个组以上.d-c记为
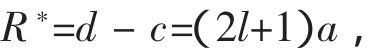
我们把R*叫做闭全距.
分布数列呈钟形分布,表现对称分布.设对称轴x=μ,它拟合的密度函数为
根据样本值的情况,将其分为2i+1组,各组的范围为

并记mi为区间

内的样本数,i=0,1,…,l
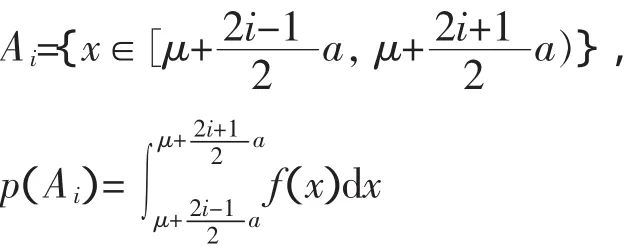
作表
此表称为样本分组频数分布表.显然
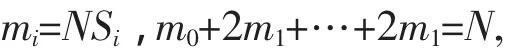
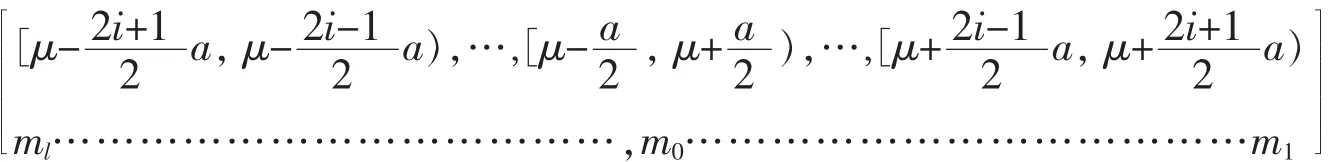
得到的直方图见图1.

图1 直方图
且有
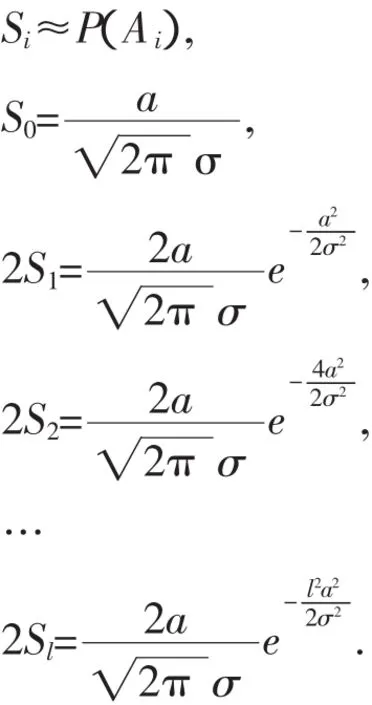
取对数:
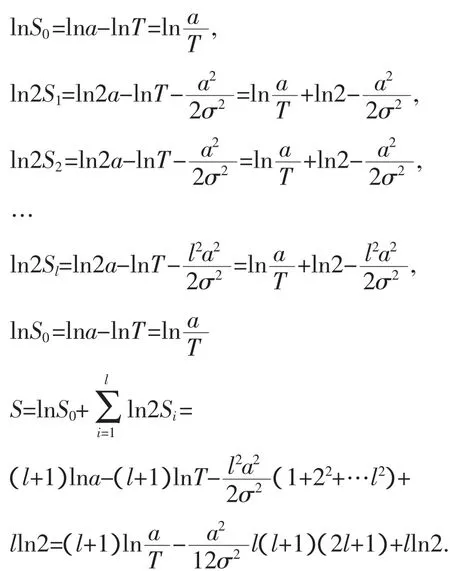
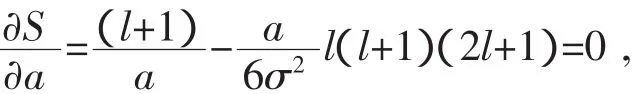
得
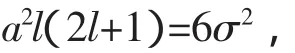
由此等式

这里a取极大值,应满足的条件:
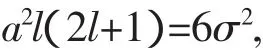
a取一般值可写为:

(1)两边同乘以2得:
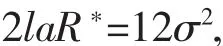
又
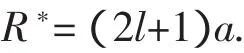
进而有
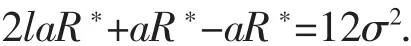
即
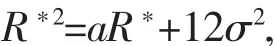
当然有

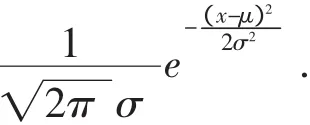
定理1一组数据呈正态分布,它拟合得密度为单调递减的函数.l固定,S有极大值,而没有极小值对a求偏导:
已知闭全距为R*,等距分类,组距极大值满足(1).
1.2 由等式(1)推导a的上界
由直方图,共2l+1个;Si(0,1,…,2l)中,所有数据分布在内,99.7%分布在(μ-3σ,μ+3σ)内.所以有

因为l≥2,故

进一步

又因为(1),又有

当l≥3时,有

当l≥4时,有

2 主要定理的证明
2.1 定义
定义3N个数据分布R*上表示每个数据所占平均距离.
2.2 主要定理的证明
E.贝肯巴赫所著《不等式入门》,有些不等式我们常用,故作为一个引理.
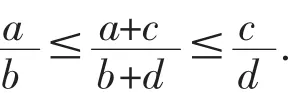
引理2N个数据依正态分布,R*是闭全距,每个数据所占的平均距离为.则有i,使得
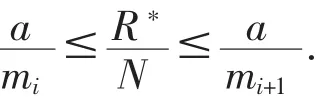
定理1一列正态分布的数列,则至少有2个相似区间.
证明依引理2,有

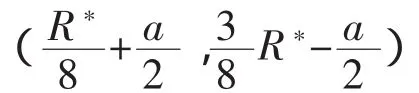
定理2正态分布的树立在中存在一个相似区间,这里a表示组距.
所以M内有一个相似区间.由于对称性还有一个相似区间.
3 利用定理3,可找出求组距方法
1)把资料从小到大排列.并计算资料组的平均数μ,方差σ.
2)求出闭的全距R*并计算
3)s1…sn个数分别为.不妨设满足
5)一份资料分组的时候,应注意组与组的衔接.衔接好了,体现整体的趋势.设数据链为:b0≤b1≤…≤bn≤bn+1…其中一组包括了b1,b2,bn,如何截取才能使这一段嵌入数据链中去呢?我们规定:这一组应包括在(a,c)内,其中:
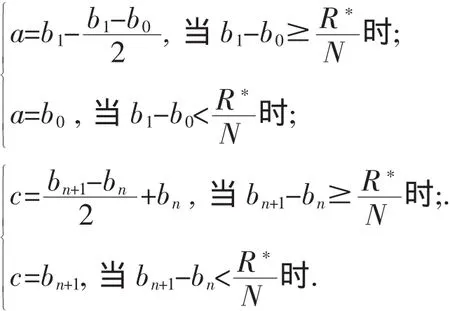
6)若遇到偏态分布,也用上面的方法处理,也不过作两次,可参看下列例子.
4 例子
对城市居民的家庭生活情况抽样调查,得到54户家庭人均月收入的资料.
1) 已排列的54户家庭人均月收入资料


本组资料最小值为810,最大值为2380.本组资料均值

c=800,d=2400,闭全距为
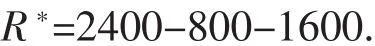
2)因为它不是完全对称,分成两个步骤.从800到1497.2共有27个数据,27个数据之间的平均距离
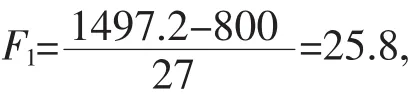

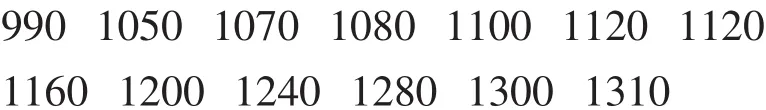
这13个点每个点所占平均距离,应考虑区间为

说明选相似区间时,向右倾斜.所以在下面的讨论中删去990.
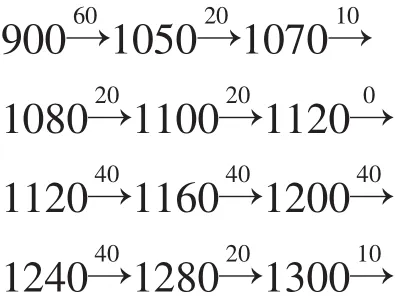
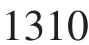
等价于:
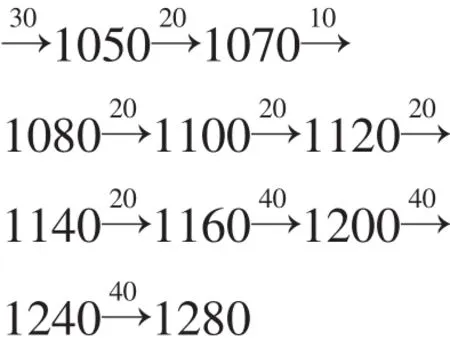
进一步我们可以确定:1148.6右边的点至多是2个点.即1160,1200
若不然,右边有3个点,那么左边的点必须有3×2.45=7.35个点才能平衡,而这是不能的.
因为左边的点共有6个点:1050,1070,1080, 1100,1120,1120
不难发现在(1020,1220)内共有8个数据,它们是:1050,1070,1080,1100,1120,1120,1160 1200.
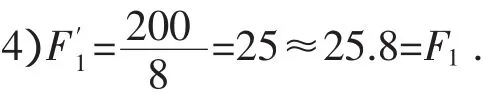
故(1020,1220)为相似区间.S=8,a可选200.
5)令y=x-μ从1497.2到2400,共有27个数据,27个数据之间平均距离:

半全距
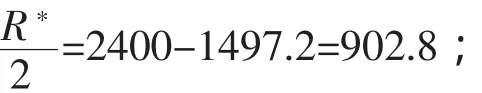
而这个点在资料数据中没有,所以叫做虚坐标,它位于1940与1970之间.
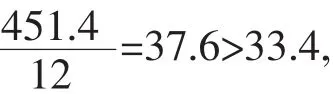
不难看出在1800~2000之间共有六个数据,1840,1860,1870,1880,1940,1970,
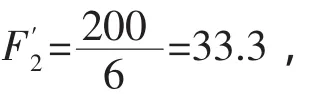
它与F2=33.4相似(F′2≈F2).
故1800~2000之间的六个数据组成相似区间.S=6.相似区间应选(1805~2015),可结合取整的方式进行可选(1800~2000).此种方法已被多数人认可.
7)设a′为组距,那么6×33.4=200.4,为a′的估值.而a′的上界为
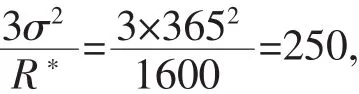
a′取值为200.
总之:由上面的结论.取200.通过进一步整理,得到分布数列:

表1 某市居民家庭人均月生活费收入次数分布表
[1]E.贝肯巴赫,R.贝尔曼.不等式入门[M].北京:北京大学出版社,1985:23.
[2]谢启南,韩兆洲.统计学原理[M].6版.广州:暨南大学出版社,1991:53-64.
[3]吴传生.概率论与数理统计[M].北京:高等教育出版社,2004:128-144.
Abstract:Because of thinking only the number of data but not fitting function,we would be adequate to take a farther afield when calculating group data with empirical formula.We have proved the three theorems based on studying the normal distribution,and then reach the conclusion there is a better method to do the same work.The method is simpler and more practical than empirical method and also work well with any skewed distribution.
key words:mean value;variance;fitting fuction;vange;quarter range
〔编辑 高海〕
The Isometric Group about Normal and the Skewed Distribution
JIA Zhen-sheng
(School of Economical Trade,Chongqing Three Gorges University,Chongqing,404000)
O213
A
1674-0874(2010)05-0005-05
2010-01-25
贾振声(1952-),男,河北徐水人,教授,硕士生导师,研究方向:数理统计.
