无序对二维声子晶体平板负折射成像的影响＊

李晓春 高俊丽 刘绍娥 周科朝 黄伯云

1)(中南大学物理科学与技术学院,长沙 410083) 2)(中南大学粉末冶金研究院,长沙 410083)

无序对二维声子晶体平板负折射成像的影响＊

李晓春1)2)†高俊丽1)刘绍娥1)周科朝2)黄伯云2)

1)(中南大学物理科学与技术学院,长沙 410083) 2)(中南大学粉末冶金研究院,长沙 410083)

(2009年1月5日收到;2009年5月4日收到修改稿)

利用多重散射理论分析了位置无序对钢/水声子晶体负折射成像的影响.发现声子晶体负折射成像与周期结构中的方向性通路有关;该方向性通路不同于一般意义上的位置波导,它是声子晶体周期散射的结果;通路中的障碍对成像有较大影响;随着散射体位置无序程度的增加,周期性散射减弱,方向性通路被破坏,成像也随之减弱,甚至消失.

声子晶体,负折射,无序,多重散射

PACC:4320,4335

1.引言

1968年,Veselago提出了左手物质的概念[1], 2000年,Smith等人从实验上实现了负折射[2,3],而Pendry关于负折射介质平板可以突破衍射极限完美成像的建议[4],更是激起了科学工作者对负折射研究的空前兴趣.近年来,光子晶体中的负折射现象也被陆续发现和实验证实[5,6],并进一步地,将负折射研究推广到了声子晶体[7—9].传统的球面透镜不能把光/声汇聚到小于波长平方的区域内,利用负折射制成的透镜则可以克服这个局限,而且,平板透镜的加工精度也远高于普通的球面透镜,因此,通过负折射实现平板成像的应用前景是非常诱人的.

但是,对于负折射成像的机理目前尚无定论.负折射是作为介质的属性存在,还是一种特定条件下的偶然现象,这个问题还没有明确的答案.若负折射作为介质的属性存在,即存在所谓的负折射物质,那么它是否与物质的其他属性一样,只与物质的种类有关,而与物质的结构无关呢?若这样,它应该是均匀的、各向同性的(至少相对于入射波的波长尺寸来说是这样的).但是,到目前为止,文献[10]报道的负折射物质是具有周期结构的,其他报道的具有负折射现象的光子晶体、声子晶体也是周期结构的[7,8].周期结构具有各向异性,但各向异性不是周期结构独有的特性.若负折射物质只能是各向异性的介质,则各向异性的情况就太多了.而且,各项异性是如何导致负折射的,也不甚清楚.有人认为光子晶体中的负折射现象是一种普通的波导行为,或自准直效应,只是它们在效果上表现出负折射的特征[11].如果各向异性是形成负折射现象的决定因素,那么,散射,特别是周期性散射的作用何在?为此,本文通过在周期结构中引入无序,减少结构的各向异性,分析无序对负折射成像的影响,以期对二维声子晶体平板成像机理进行探讨.

2.基本模型

以二维钢/水声子晶体为模型,钢圆柱按正三角形方式排列在基体水中.材料参数为ρ水=1.0×103kg·m-3,cl=1.49×103m·s-1,ct=0 m·s-1;ρ铁= 7.67×103kg-3,cl=6.01×103m·s-1,ct=3.23×103m·s-1.用多重散射方法[7]计算无限周期情况下钢/水声子晶体的带结构.结果如图1(a)所示:体系具有部分带隙,在频率0.65—0.98范围,M—K方向为带隙,Γ—M方向为通带.图1(b)是对应结构的第一布里渊区等频线.负折射可以根据带结构和等频线来推断,接近圆形的等频线能得到负折射成像[8].从图1(b)可以看出,在频率0.65—0.95之间,声子晶体第二条带中的等频线都接近圆形,且这些等频线随频率的增加朝圆心移动,在这个频率范围内,声子晶体有效折射率为负值.

实际应用的声子晶体都是有限的.为此,以9层声子晶体平板为模拟对象,计算声场的分布.y方向单层板沿水平方向上(即x方向),按正三角形排列成9层,并置于水中.单层有44/45个散射柱体,9层板共400个柱体,柱体大小同图1.空间上,从左到右,依次为水、平板、水.图2给出了声波通过9层声子晶体平板后的透射情况,其中,lnT=ln(P/P0). P(r)为空间任意处的声压,P0为无平板时该处的声压[9],实际计算lnT时,取该点P,P0的平均值.可以看出,图2(a)中,0.66—0.90频带对应Γ—M方向的导带:图2(b)中,0.68—1.1和1.24—1.45频带对应M—K方向的禁带.这表明9层声子晶体平板具有部分带隙.对比图1(a)中的Ⅰ,Ⅱ区和图2 (b)中的Ⅰ,Ⅱ区,发现9层平面板与无限周期情况下的带结构基本相同.这种一致性说明了本文使用的有限场理论是合适的.图2中的带隙位置与图1 (a)比较,存在些许差异,可认为是有限层板和无限层板之间的差异造成的.

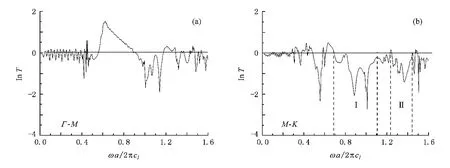
图2 三角形排列铁/水声子晶体9层平板透射谱 (a)Γ—M方向;(b)M—K方向(填充率F=0.403.cl为水的纵波波速)

图3(a)给出了声波通过9层声子晶体平板的声场分布图.点声源位于(0,0)处,沿Γ—M方向穿过声子晶体平板.从图中可以看出:在平板内部和平板后面都有一个像点,其成像过程可由图3(b)示意.对于0.685频率的声波,9层声子晶体平板给出了负折射特点的成像.像在x方向有一定的强度分布,这可能与不同入射角成像位置[12]不同有关,与几何光学成像中,近轴光线和远轴光线成像会有像差是一致的.

无疑,频率0.685附近的部分带隙,对于此处的负折射成像起了重要作用,但Γ—M方向的导带是否意味着存在该方向的波导呢?若存在,这样的波导性质如何?为此,改变周期结构中柱体的位置,在可能的通路上引入路障,直至引入位置的随机无序,考察成像的变化.

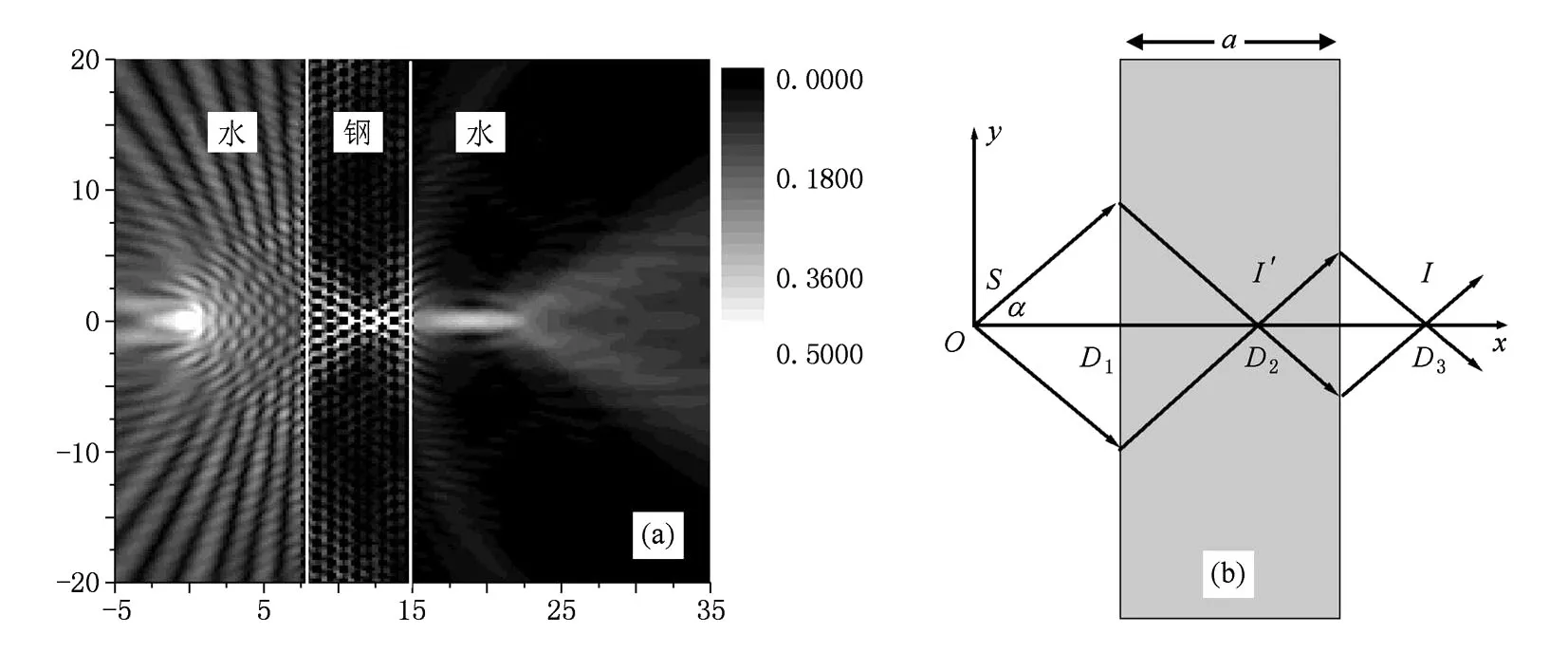
图3 9层声子晶体负折射成像图 (a)点声源通过9层声子晶体声场分布图;(b)成像波路示意图(填充率F= 0.403;频率f=0.685)

3.路障模型

由于Γ—M方向为导带,在声波可能的通路上,有针对性地设置路径障碍.为此,将靠近x轴的,关于x轴对称的第2层某些柱体,向x轴移动半个长度单位(晶格常数a为一个长度单位),形成通路中央障碍,考察其成像情况.图4是几种典型路障下的成像情况.

图4 路障模型成像 (a)无路障规则模型;(b)两柱体路障;(c)四柱体路障(填充率F=0.403,频率f=0.685)

图4表明,从规则排列到两柱体障碍、四柱体障碍,随着第二层形成障碍的柱体增多,成像逐渐变得模糊.近x轴、关于x轴对称的4个柱体(x轴上下方共8个柱体),向x轴移动半个长度单位,形成障碍后,像基本消失(见图4(c)).进一步分析表明,远离x轴的柱体移动对像的影响不大.这可能与大角度信号在远轴处耦合进入平板的信号较弱有关.由于信号耦合进入平板的程度不一样,近轴信号对像的贡献要远大于远轴信号的贡献.

以上结果似乎说明了波导的存在.但仔细分析,这样的通路不同于一般的位置波导(通路在某个特定位置上).它更象是方向性波导,即在某个方向上都存在通路.仔细查看图3(a)和图4中的像,发现它们都已显示出了‘线’像的特征.这正是方向性波导的特点.因为,在方向性波导中,对于在y方向有足够长度的声子晶体平板,一定范围内的小角度入射信号耦合进入平板的能量相差不大,这样,不同位置同一方向的通路就会会聚成一‘线’像.随着入射角度的增大,耦合进入平板的能量减少,所以大角度信号对像的贡献大为减少,造成‘线’的截断.但是,这样的方向性波导似更应该归于周期性散射的结果,而不同于一般意义上的位置波导.因为只有周期性散射,才会出现通带和带隙.而部分带隙的存在,意味着同一频率的信号,在不同方向上出现了导通和禁通的传播差异,这就为出现负折射特征的成像提供了可能.因此,周期性散射及部分带隙才是负折射特征成像的根本原因.周期性减弱,成像变差,甚至像消失.下面关于随机无序的分析也认证了这一点.

4.随机无序模型

设某柱体的原位置为r0,引入无序后,该柱体的位置变为r=r0+δ,δ为无序平移量,亦即无序度.体系给定某个δ值后,各柱体在δ值范围内,可向空间各个方向任意移动,具体移动情况由随机函数确定.δ最大取值受柱体不重叠限制,因此,低填充率系统,δ取值范围大.本文中的平板结构,在填充率F=0.2时,对频率f=0.7的信号也有比较好的负折射成像,见图5(a).且其最大无序度(δmax= 0.265)较填充率F=0.403的体系大,更适合调查无序对成像的影响.因此,以填充率F=0.2的体系为模型,考察其9层声子晶体平板在不同无序度下的成像情况.结果见图5.

图5 填充率F=0.2体系在不同无序度下的点源成像(δ为无序度,点源频率f=0.7) (a)δ=0;(b)δ= 0.106;(c)δ=0.212;(d)δ=0.265

从图5(b),(c),(d)中可以明显看出,随着无序程度的增加,负折射成像逐渐减弱.在最大无序δmax=0.265时,图5(d)中的像基本消失.对不同填充率体系的调查发现:不同的填充率结构,负折射像消失的速度是不一样的.对高、低填充率模型的比较发现,随着无序度增大,小填充率模型的像更容易受到破坏.这可能与小填充率模型半径较小,无序变化幅度大,周期性结构更容易被破坏有关.

5.结 论

通过本文模型中的负折射成像研究发现,声子晶体中负折射特征的成像与周期性结构和方向性带隙有密切关系.周期性结构导致导带和带隙的出现,而部分带隙的存在,导致了入射波传播的各向异性.这种各向异性,表现为在晶体中出现一些方向性通路.这种方向性通路是周期散射的结果,方向性通路不仅与结构的排列有关,而且与插入体、基体的材料,以及材料弹性性质有关.无序结构通过破坏结构的周期性而影响部分带隙,并因此影响方向性通路,进而影响成像.随着无序程度的增加,周期性减弱,负折射特征的成像也随之减弱,甚至消失.材料及其结构的周期性散射是负折射成像的主要原因.针对带隙材料,设计适当的周期结构和部分带隙,可以实现在某些频段的负折射特征的平板成像.

[1]Veselago V G1968Sov.Phys.Usp.10 509

[2]Smith D R,Padilla WJ,Vier D C,Nemat-Nasser S C,Schultz S 2000Phys.Rev.Lett.84 4184

[3]Shelby R A,Smith D R,Schultz S 2001Science292 77

[4]PendryJ B 2000Phys.Rev.Lett.85 3966

[5]Cubukcu E,Aydin K,Ozbay E,Foteinopoulou S,Soukoulis C M 2003Nature423 604

[6]Moussa R,Foteinopoulou S,Zhang L,Tuttle G,Guven K,Ozbay E,Soukoulis C M 2005Phys.Rev.B 71 085106

[7]Qiu C Y,Liu Z Y,Mei J,Ke M Z2005Solid State Commun.134 765

[8]Ke M Z,Liu Z Y,Qiu C Y,Wang W G 2005Phys.Rev.B 72 064306

[9]Li S,George Thomas F,Chen L S,Sun X,Kuo C H 2006Phys. Rev.E 73 056615

[10]Zhang Y,Fluegel B,Mascarenhas A 2003Phys.Rev.Lett.91 157404

[11]Kuo C H,Ye Z 2004 cond-mat/0312288

[12]Li GJ,Kang X L,Li Y P 2007Acta Phys.Sin.56 6403(in Chinese)[李国俊、康学亮、李永平2007物理学报56 6403]

PACC:4320,4335

Disorder effect on the focus image of phononic crystal panel with negative refraction＊

Li Xiao-Chun1)2)†Gao Jun-Li1)Liu Shao-E1)Zhou Ke-Chao2)Huang Bo-Yun2)

1)(School of Physics and Technology,Central South University,Changsha 410083,China)
2)(Powder Metallurgy Research Institute,Central South University,Changsha 410083,China)

5 January 2009;revised manuscript

4 May 2009)

By multiple-scattering theory(MST),disorder effect on the focus image in steel/water phononic crystal panel with negative refraction was investigated.It wasfound that sonic waves within certainfrequency range can propagate along certain directions in periodic crystal andform a focus image with negative refraction characteristics.These directional pathways dependon the periodic scattering in the crystal and are different from the ordinary positional guide.Obstacles in pathways have a deep influence on the focus image.With the increasing of degrec of positional disorder of cylinders,the periodic scattering decreases,pathways are broken,and the focus image becomes blurred or disappears.

phononic crystal,negative refraction,disorder,multiple-scattering

＊中南大学博士后科学基金资助的课题.

†E-mail:lxc4805@mail.csu.edu.cn

＊Project supported by the Central South University Science Foundation for Post-doctoral Scientists of China.

†E-mail:lxc4805@mail.csu.edu.cn