关于Birkhoff表示的Lagrange像的研究

丁光涛

(安徽师范大学物理与电子信息学院,芜湖 241000)

关于Birkhoff表示的Lagrange像的研究

丁光涛†

(安徽师范大学物理与电子信息学院,芜湖 241000)

(2009年3月14日收到;2009年3月27日收到修改稿)

研究运动微分方程Birkhoff表示的Lagrange像.得出二阶Lagrange函数应满足的条件,在此条件下广义Lagrange方程为二阶微分方程组;提出新的求解Lagrange力学逆问题路线;指出在此问题研究中曾发生过的失误.举例说明所得结果的应用.

Birkhoff表示,Lagrange像,逆问题,二阶Lagrange函数

PACC:0320

1.引言

Birkhoff提出一类新型动力学方程,Santilli建议命名为Birkhoff方程并进行了深入研究[1,2].20多年来,对Birkhoff方程的研究成为国内外数学力学界一个重要的热门课题,特别是我国学者在此领域进行了多方面多层次的深入研究,并取得一系列丰硕的成果[3—18],文献[4]及其所附的大量参考文献系统总结又全面展示Birkhoff系统动力学的研究进展.

文献[2]中提出了关于Birkhoff表示的Lagrange像的问题,把Birkhoff动力学函数与二阶Lagrange函数以及Lagrange力学逆问题联系起来,但在研究中有值得商榷之处.本文继续研究这方面的问题,结果表明作为Birkhoff表示的Lagrange像的二阶Lagrange函数,满足一定条件时,导出的广义Lagrange方程仍为二阶微分方程组,而且这种二阶Lagrange函数容易变换成传统的Lagrange函数,从而构成解决Lagrange力学逆问题新的路线图,此外,讨论中对文献[2]中的失误进行了修正.最后,举例说明得到的结果.

2.Birkhoff表示及其Lagrange像[2]

设系统的运动微分方程为

引入新变量使方程降阶,取

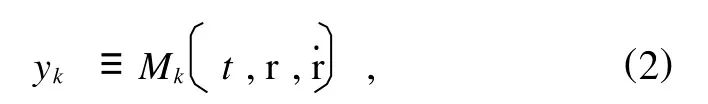
变换满足规则性条件,即

故由(2)式能反解出

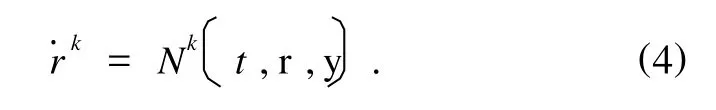
代入(1)式得到

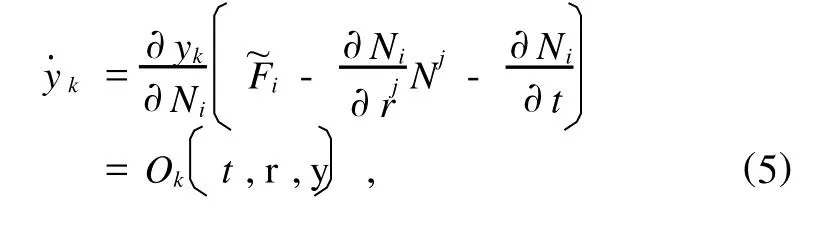
式中

这样二阶微分方程组就变换成一阶微分方程组,引入统一的变量将(4)和(5)式写成

方程(7)可以表示成Birkhoff方程形式[2,3,18],即

式中B为Birkhoff函数,Rμ为Birkhoff函数组.定义Birkhoff张量

规则的Birkhoff系统满足下列条件:

则由(10)式可以解出

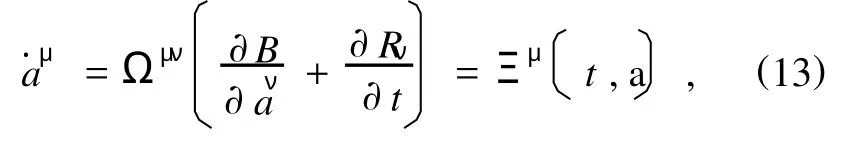
其中Ωμν为Birkhoff逆变张量,满足下列条件:

将变量aμ分解成原来的两组变量rk和yk,并设Birkhoff系统满足下列条件:

则该系统为严格规则系统,对此系统可解得(2)式的结果.

对严格规则的Birkhoff系统,Pfaff-Birkhoff作用量可以作如下变换[2]:

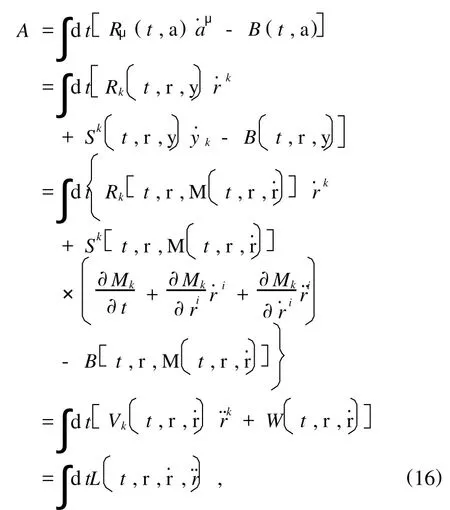
式中L为二阶Lagrange函数

(16)式的过程,完成了Birkhoff系统的Pfaff-Birkhoff作用量到等价的二阶Lagrange作用量的变换,即得到了Birkhoff表示的Lagrange像.

3.广义Lagrange方程为二阶微分方程组的条件

将(17)式中L代入广义力学的Lagrange方程,得到

在一般情况下,方程(21)是三阶微分方程,而且含有加速度的非线性项.如果L满足下列条件[19]:

则方程(21)中的三阶微商项和二阶微商非线性项同时抵消为零,即广义力学的Lagrange方程仍然为二阶线性微分方程

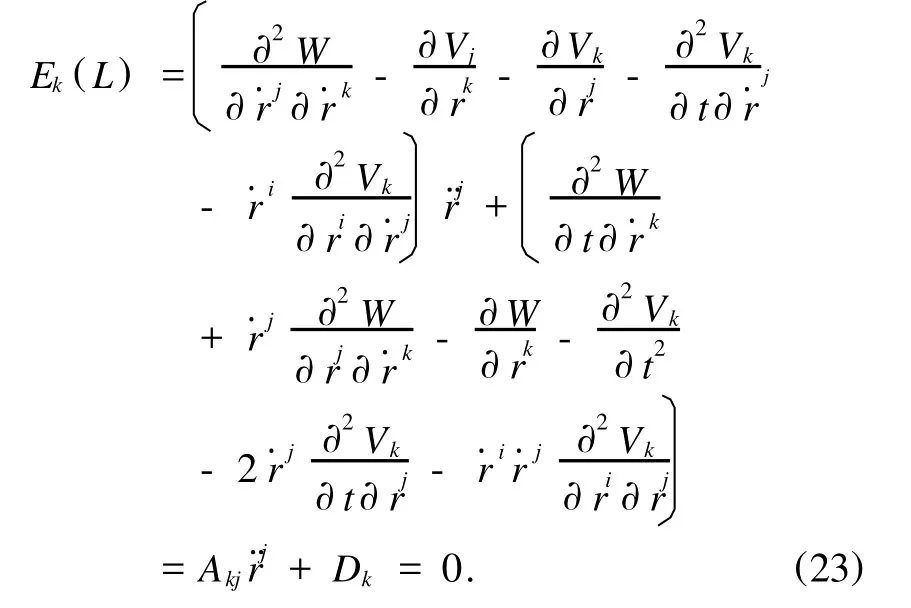
条件(22)成立,意味着

反之,若(25)式满足,则条件(22)成立.(25)式成立表明(17)式L中r¨i的线性项可以利用广义力学中规范变换消去,从而得到通常位形空间中传统的Lagrange函数[19,20],即

Lagrange力学逆问题研究对给定的微分方程能否导出相对应的Lagrange函数,从而将方程改写成等价的Lagrange方程形式.上述结果给出了二阶微分方程组Lagrange化的一种新的路线图:二阶微分方程组—一阶微分方程组—Birkhoff表示—Lagrange像(二阶Lagrange函数)—位形空间中Lagrange函数.

应当指出,文献[2]中提出了Birkhoff表示的Lagrange像问题,也指出了与Lagrange逆问题相关,但是研究过程中有失误.在计算与二阶Lagrange函数对应的Lagrange方程时,文献[2]中写成

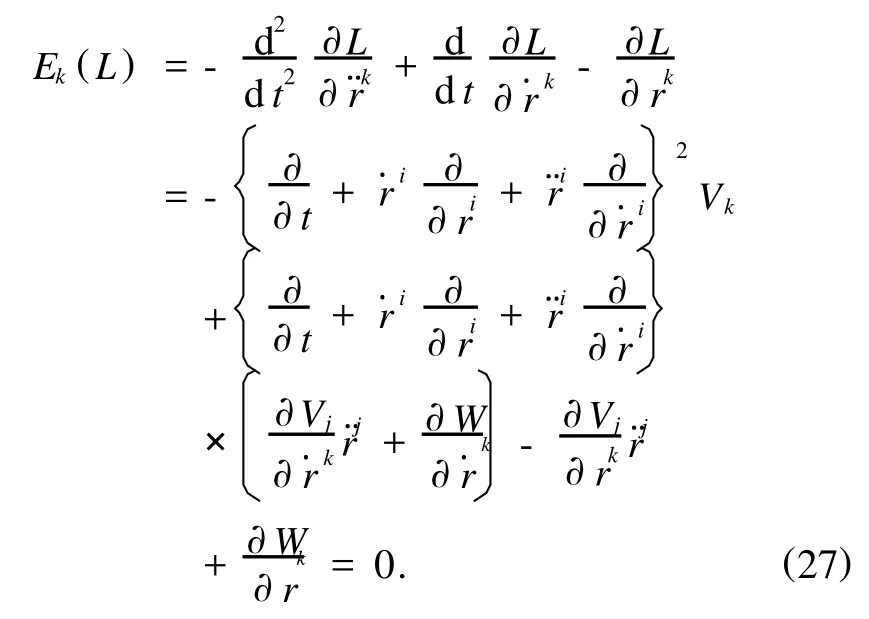
然后据此指出上述展开式是二阶微分方程组,而不是预期的三阶微分方程组;进一步又指出,当全部Vk均与速度无关时,上述展开式才是加速度的线性方程组.事实上,方程式(27)不能成立,直接将它开展得到的结果与(21)式相比较,恰恰缺失了含r…j的项.产生这个错误的根源在于(27)式中将对t的全微商写成

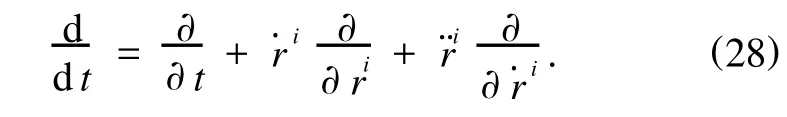
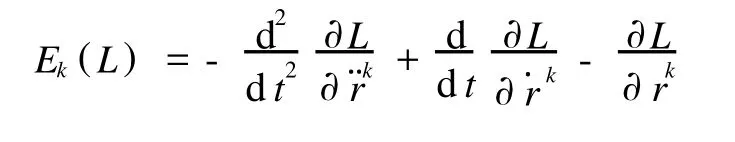
将上式直接计算展开,得到的结果与(21)式一致,在一般情况下,是三阶微分方程组,只有在满足条件(22)时,(29)式才是二阶线性微分方程组.文献[2]中要求全部Vk均与速度无关过于严格了,因为这个要求只是使条件(22)成立的特殊情况.

4.算例

例1 微分方程为

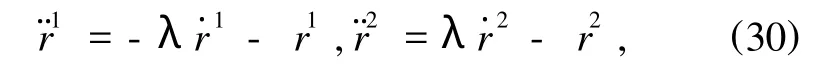
引入变量y1和y2,将上述方程化为一阶方程组

引入统一的变量

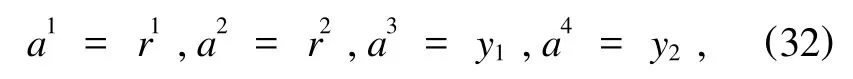
将方程(31)改写为

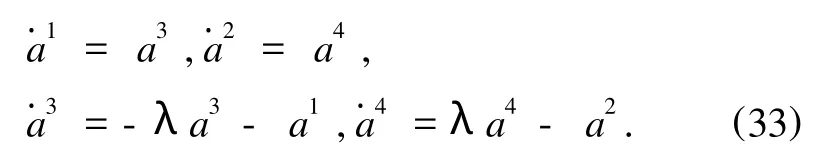
利用文献[18]的方法一,容易求得Birkhoff函数和Birkhoff函数组为

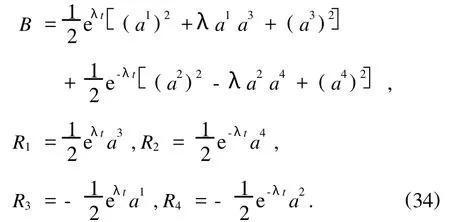
容易证明这是严格规则的Birkhoff系统,其Pfaff-Birkhoff系统作用量为

按照(16)式中程序,得到上述作用量的Lagrange像为

即系统的二阶Lagrange函数为

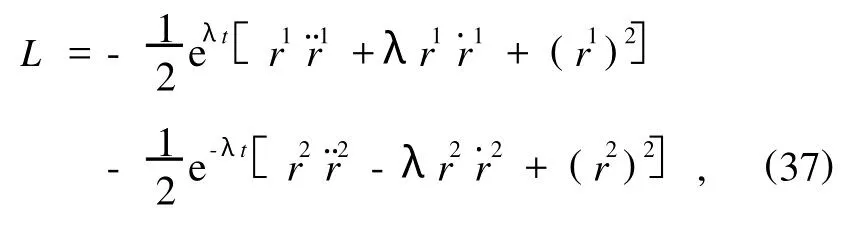
条程件为(22)成立,由上述L导出的广义Lagrange方

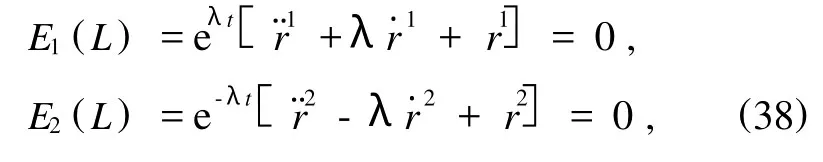
与方程(30)等价.

引入规范变换函数

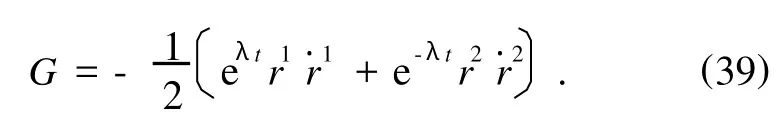
由(29)式得位形空间Lagrange函数为

而由L¯导出的Lagrange方程正是方程(38).

例2 Hojman-Urrutia方程[2,3,21]

引入变量

系统(41)与下列一阶方程组等效:

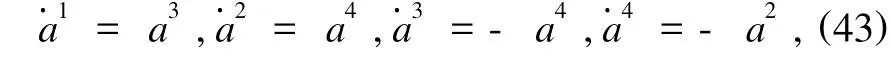
系统(43)的一个Birkhoff表示如下:

定义新变量

容易证明,系统是严格规则的,按(16)式程序,由其Pfaff-Birkhoff作用量导出Lagrange像

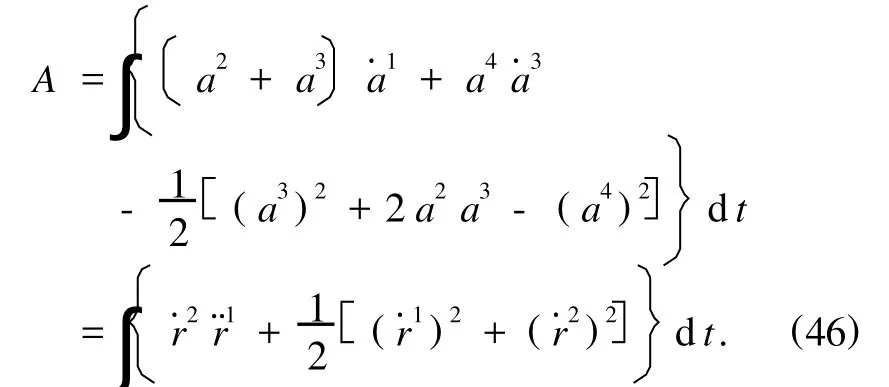
系统的二阶Lagrange函数

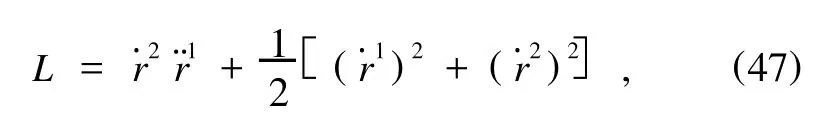
显然,对上述Lagrange函数条件(22)不成立,导出的广义Lagrange方程为

这是三阶微分方程,写成原始变量形式为

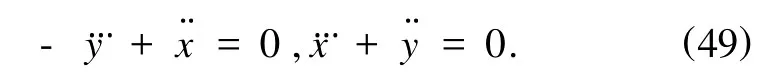
这不是原方程(41),但是可由(41)导出.

若将(47)式代入(27)式,则得到

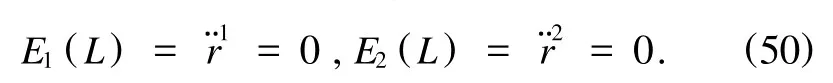
这是二阶微分方程,但是错误的.然而,若将(47)式中L代入修正后的(29)式,则得到与(48)式相同的结果.

应当指出,Hojman-Urrutia系统是一个典型的例子,它不能化成自伴随的形式,因而也不能有通常的Lagrange表示.本例中这个系统虽然从Birkhoff表示的Lagrange像,得到二阶Lagrange函数,但由于不满足条件(22),故不能由此而导出位形空间中通常的Lagrange函数.

[1]Birkhoff G D 1927Dynamical systems(Providence R I:AMS College Publ.)

[2]Santilli R M 1983Foundations of Theoretical Mechanics(Ⅱ)(New Y ork:Springer-Verlag)

[3]Mei F X,Shi R C,Zhang Y F,Wu H B 1996 Dynamics of Birkhoffian System(Beijing:Beijing Institute of Technology Press) (in Chinese)[梅凤翔、史荣昌、张永发、吴惠彬1996 Birkhoff系统动力学(北京:北京理工大学出版社)]

[4]Luo S K,Zhang Y F 2008Advances in the Study of Dynamics of ConstrainedSystems(Beijing:Science Press)(in Chinese)[罗绍凯、张永发等2008约束系统动力学研究进展(北京:科学出版社)]

[5]Mei F X 2004Symmetries and Conserved Quantities of Constrained Mechanical Systems(Beijing:Beijing Institute of Technology Press) (in Chinese)[梅凤翔2004约束力学系统的对称性和守恒量(北京:北京理工大学出版社)]

[6]Mei F X 1993Sci.ChinaA 36 1456

[7]Wu HB,Mei F X1995Chin.Sci.Bull.40 885(in Chinese)[吴惠彬、梅凤翔1995科学通报40 885]

[8]Mei F X 1999Chin.Sci.Bull.44 318(in Chinese)[梅凤翔1999科学通报44 318]

[9]Zhang Y2001Acta Mech.Sin.33 669(in Chinese)[张 毅2001力学学报33 669]

[10]Luo S K,Chen X W,Guo Y X 2002Chin.Phys.11 429

[11]Chen X W,Luo S K,Mei F X 2002Appl.Math.Mech.23 53

[12]Luo S K2003Appl.Math.Mech24 468

[13]Zhang H B,Chen L Q,Gu XL 2004Acta Mech.Sin.36 254(in Chinese)[张宏彬、陈立群、顾书龙2004力学学报36 254]

[14]Zhang Y,Fan C X,Ge W K 2004Acta Phys.Sin.53 3644(in Chinese)[张 毅、范存新、葛伟宽2004物理学报53 3644]

[15]Xu Z X 2005Acta Phys.Sin.54 4971(in Chinese)[许志新2005物理学报54 4971]

[16]Mei F X,Gang T Q,Xie J F 2006Chin.Phys.15 1678

[17]Ge W K,Mei F X 2007Acta Phys.Sin.56 2479(in Chinese) [葛伟宽、梅凤翔2007物理学报56 2479]

[18]Ding G T 2008Acta Phys.Sin.57 7415(in Chinese)[丁光涛2008物理学报57 7415]

[19]Ding G T 2009Acta Phys.Sin.58 3620(in Chinese)[丁光涛2008物理学报58 3620]

[20]Ding G T 2009Acta Phys.Sin.58 6725(in Chinese)[丁光涛2008物理学报58 6725]

[21]Hojman S,Urrutia L F 1981J.Math.Phys.22 1896

PACC:0320

A study on the Lagrangian image of the Birkhoffian representations

Ding Guang-Tao†

(College of Physics and Electronic Information,Anhui Normal University,Wuhu 241000,China)

14 March 2009;revised manuscript

27 March 2009)

The Lagrangian image of the Birkhoffian representations is studied.The conditions that the second-order Lagrangians should satisfy are obtained,under which the generalized Lagrange equations are second-order differential equations.A new way for solving the inverse problem in Lagrange mechanics is presented.An error made in the study by some author is pointed out.Two examples are given to illustrate the application of the result.

Birkhoffian representations,Lagrangian image,inverse problem,second-order Lagrangian

†E-mail:dgt695@sina.com

†E-mai:dgt695@sina.com