二维颗粒体系单轴压缩形成的力链结构*
2010-09-19孙其诚王光谦张国华
孙其诚 金 峰 王光谦 张国华
1)(清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
2)(北京科技大学物理系,北京 100083)
二维颗粒体系单轴压缩形成的力链结构*
孙其诚1)†金 峰1)王光谦1)张国华2)
1)(清华大学水沙科学与水利水电工程国家重点实验室,北京 100084)
2)(北京科技大学物理系,北京 100083)
(2009年4月5日收到;2009年4月22日收到修改稿)
从接触力、能量分布和接触网络结构特点出发,提出了强力链的力大小(Fc)判据(Fc大于平均接触力〈F〉)和角度θc判据(θc=180/〈Z〉,其中〈Z〉是平均配位数),指出强力链和弱力链是本质不同的两类结构存在于颗粒体系中,其中强力链网络与体系的宏观性质直接相关.以二维颗粒体系的单轴压缩为例,计算发现了强力链长度的幂率分布规律,分析了侧向压力系数与相应强力链网络结构的关系:当内部强力链网络充分发育而不再变化时,侧向压力系数趋于稳定数值.
颗粒物质,力链,多尺度结构
PACC:0320,4610
1.颗粒物质中的力链
颗粒物质是大量离散的固体颗粒相互作用而组成的复杂体系,普遍存在于自然界.颗粒体系具有非连续和非均匀的基本特征,颗粒间作用力一般大于间隙气体或液体力而起主导作用,形成颗粒→力链→体系的多尺度结构,决定着体系的静力学和动力学性质.
早期,人们用实验检测体系局部的颗粒排布规律并建立起它与宏观力学行为的联系,比如Oda将砂土的三轴压缩试验试样经固化处理后从不同的方向切成薄片,然后观察颗粒接触点角的分布,发现颗粒接触点角向大主应力方向集中[1];Matsuoka基于光弹材料及圆铝棒的直剪试验结果,从颗粒接触点角变化规律出发推导出滑动面上的应力剪胀关系方程[2].在土力学中,土体与结构接触面的力学特性涉及到大变形、局部不连续等问题,张嘎等采用数字图像技术分析从微观角度观察和测量加载过程中结构面附近土颗粒的运动[3],分析了观测接触面的应变局部化及剪切带形成,分析了接触面的变形机理、确定接触面厚度等.1979年Cundall和Strack[4]提出了离散元法(distinct element method,DEM),DEM逐渐成为颗粒体系微观结构研究的有效工具,它能提供颗粒的位移和接触力等详细信息,进而确定体系的应力、接触力分布、接触角分布、接触时间数、组构张量、配位数等统计力学和几何参数,并由此描述宏观力学性质[5—7].DEM的优势在于研究颗粒体系的共性问题,阐述内在机理,比如土体应力剪胀、湿化机理、斜坡破坏机理和砂土剪切带形成及发展规律等,尚不能直接用于具体的工程问题.所以,近期颗粒物质研究的主导思想应该是基于固体接触力学、流体力学和统计物理等学科,建立起颗粒体系宏观力学性质的微观理论,并能够为工程技术提供所需颗粒体系的性能参数,为土力学、泥沙运动力学和泥石流等学科的发展创造条件.
在若干光弹实验和DEM模拟中发现,颗粒非连续和非均匀的排布从而形成复杂接触网络,是荷载传递的路径.力链是颗粒物质研究中的一个重要概念,Dantu开展的光弹实验中指明了颗粒内部力分布的非均匀性,发现强力链形成树状结构[8];Horne于1965年提出了solid paths的概念[9],Edwards和Oakeshott于1989年提出颗粒物质中存在架拱现象[10],Bouchaud和Cates等深化了这一概念[11],明确提出力链概念.近10年来,人们主要对接触力大小进行了大量实验测量,比如采用高精度电子天平称重法、显色灵敏复写纸压痕方法和光弹性方法等检测颗粒物质中某一截面上的接触力分布情况.但是,实验方法存在的主要缺陷是无法检测弱接触力,不能对颗粒物质内部接触力进行无干扰检测.
人们逐渐意识到力链作为一准静态结构对宏观力学性能的影响,但是往往难以采取合适的方法去观测力链,通常在颗粒体系上有控制的施加干扰,研究颗粒体系所呈现的独特规律,反馈出力链受扰动后的演变.比如采用力学谱技术[12],研究了砂土振动能量耗散的振幅谱、深度谱和频率谱,得到了在微剪切振动下颗粒微观构型和力链结构转变的证据,这是探测颗粒体系力链分布规律的一种有效手段. Sanfratello等[13]采用磁共振弹性成像技术(magnetic resonance elastography,MRE)观测和初步描述了三维力链.采用DEM方法,则可以更清晰地描述力链形态,如图1所示的点力方向变化时力链的响应.
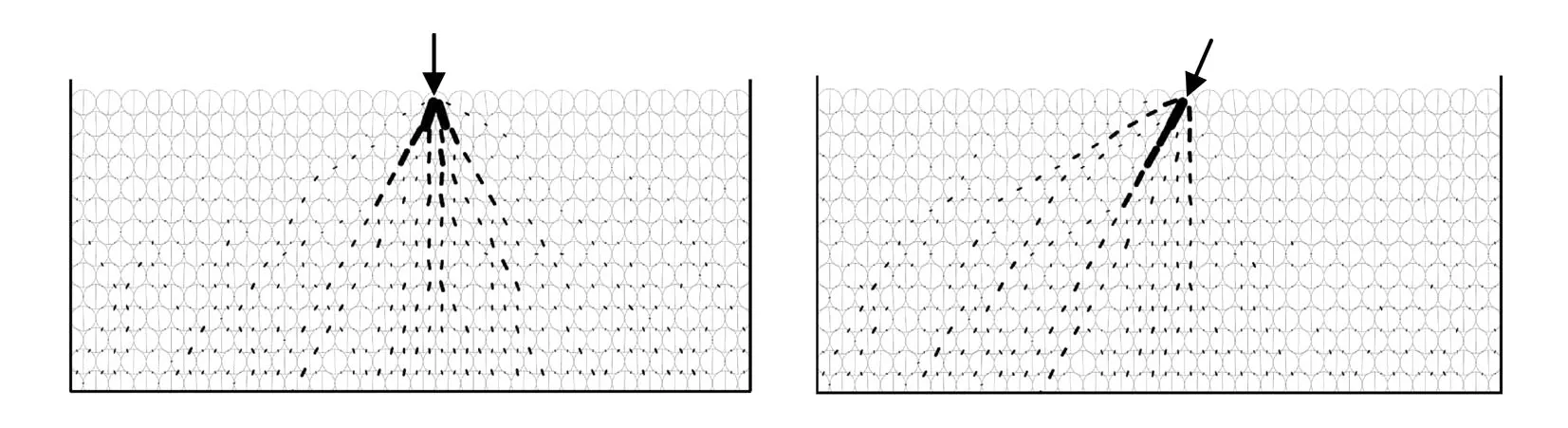
图1 在点力作用下,二维颗粒体系内力链形态随点力方向发生变化(源自文献[14])
力链不同于接触力分布、接触角分布、组构张量和配位数等局部单元的力学和几何参数统计信息,力链是应力传递路径,贯穿了若干单元,它更深刻地揭示了颗粒体系的结构层次与力学性质的关系,比如外荷载加载方式、体系尺寸、颗粒无序排布和颗粒物性参数等决定了力链结构、而力链结构网络决定了体系的应力传播模式;当外荷载力增大时,力链发生断裂和重构的数目和频率等逐渐增加,则体系可能发生破坏时,从固态演变为流态.这里需要说明的是,力链是应力传播路径,在外荷载影响下力链发生的断裂和重构是传递路径的变化(一般在d/Vr~10-5—10-7s的时间内瞬间发生,其中d和Vr分别为颗粒粒径和Rayleigh波速),此时力链发生重组,而颗粒间接触网络(亦即颗粒间的拓扑关系)未必发生变化,正如图1所示的.
我们认为力链结构及其演化是颗粒体系的主要矛盾,因此提出了颗粒→力链→体系的多尺度研究框架[15—17],其中微观尺度是组成颗粒体系的基本单元,即单颗粒,宏观尺度是指整个颗粒体系,而细观尺度则是强力链.深化力链概念,从持续时间、稳定性和能量等分析统计性质;开展数值计算和室内光弹实验量化细观尺度力链网络的几何性质,确定颗粒材料性质、级配等与力链网络几何性质的关联,恰当地刻画力链;概括力链的各种主要特征;概括地描述力链的演化,确定力链的动力学规律;描述力链网络在外荷载下的演变规律,表达出力链网络的统计效应如何影响了宏观力学性质等,都将是构建颗粒体系宏观力学性质微观理论的关键工作.
本文模拟了12400个球心共面颗粒的单轴压缩形成静态体系中的力链形态,首先提出了强力链的角度判据,发现了强力链的长度按幂率分布的统计规律.同时,本文还得到了侧向压力系数与空隙率的关系,并分析了侧压力系数与强力链能量分布的关系.
2.单轴压缩实验
图2是颗粒体系的单轴压缩示意图.本文模拟所用的颗粒体系由12400个颗粒组成,颗粒粒径分别为0.4,0.5和0.6 mm,选取沙粒的物性参数,密度ρ=2650 kg·m-3,弹性模量E=100 MPa,泊松比ν= 0.3,表面摩擦系数μs=0.3,颗粒间的黏连作用忽略不计,法向和切向接触力分别采用Hertz理论和Mindlin-Deresiewicz理论计算.左右边界距离为99.75 mm,上下边界初始距离为101.03 mm,边壁物性参数选取沙粒的物性参数.如图2所示,上下边壁相对运动压缩颗粒体系,左右边壁不动,得到不同颗粒体积份额φ的体系.当φ从0.827到0.886增加时,相应的轴向应力σzz和径向σrr也逐渐增加.对于φ为某一确定值的体系,上下边界静止.为了进行静态力链的统计分析,让体系运行足够长的时间以使得内部颗粒的动能全部耗散.
3.力链接触力判据
当半径分别为R1和R2的两球形颗粒发生接触时,接触半径为a,接触力为F和相应的弹性能W分别为[18,19]

其中1/R*=1/R1+1/R2,1/E*=(1-v12)/E1+(1-ν22)/E2,E1,ν1;E2,ν2分别为颗粒1和颗粒2的杨氏模量和泊松比,δ是颗粒间重叠量.
图3是F和W随无量纲接触力(F与平均力〈F〉的比值)的概率密度分布.内插图中的接触力分布是我们所熟知的:对于静态颗粒体系,在〈F〉附近达到最大概率密度分布,仅有40%接触点上的力大于〈N〉;更重要的是〈F〉前后力的分布规律截然不同[20,21],当F<〈F〉时,概率密度分布数值随F的增大而按幂率增加;F>〈F〉时,概率密度分布数值随F的增大而按e指数减小.从弹性能累积图可以看出,这些40%的接触点却占了80%的弹性能,这一接触力和能量分布规律与我们得到的等径颗粒体系的规律几乎一致,因此我们猜测力和能量的这一规律对于密集静态颗粒体系是普适的,基本不受颗粒物性参数、φ的影响,更进一步的工作正在进行中.
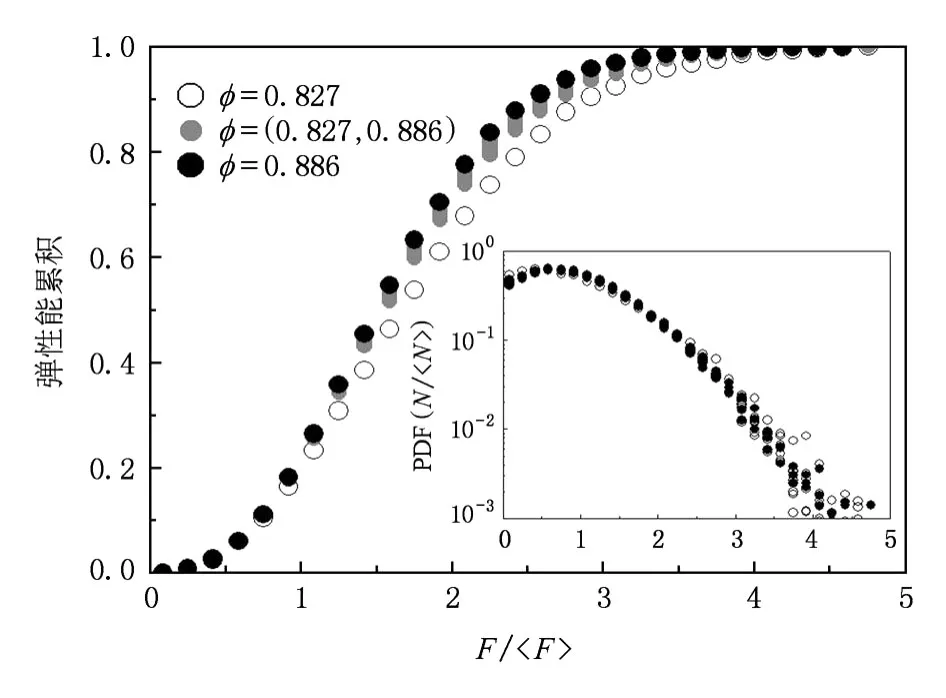
图3 颗粒弹性能累积分布(插图是接触力与接触力平均值比值的分布)
图4(a)是F>〈F〉的颗粒弹性能量角度分布,成花生形.由图4(a)可以看出:不同φ对应的弹性能量分布形状不同:φ=0.827时矮胖,而φ=0.867时瘦长,基本与体系中相应角度截面上法向应力分布一致[22]是颗粒接触面法向与水平面的夹角,见图4的示意图.当φ>0.848时,能量分布形状不再发生变化.图 4(b)为φ=0.855时,颗粒体系中总能量和的颗粒弹性能量(分别对应外围实线内区域和浅色区域)的分布情况,两者的差就是〉的颗粒弹性能量,其分布为基本为各向同性.这说明了F>的颗粒接触随着外荷载而发生相应变化,而F的颗粒接触则没有反映出外荷载的加载情况.从这个角度讲,的接触是两类本质不同的接触,颗粒接触与体系的宏观性质直接相关.
颗粒接触力分布和弹性能的角度分布(图3和图4)说明:〈F〉前后接触力本质不同,F>〈F〉的接触力链与体系宏观性质直接相关,且占据了绝大部分体系的能量.因此,可以根据力的大小把力链分为两类:强力链和弱力链,而区分强、弱力链的力判据是

即传递大于〈F〉的力链为强力链,反之为弱力链,强、弱两类本质不同的力链并存在于颗粒体系中.
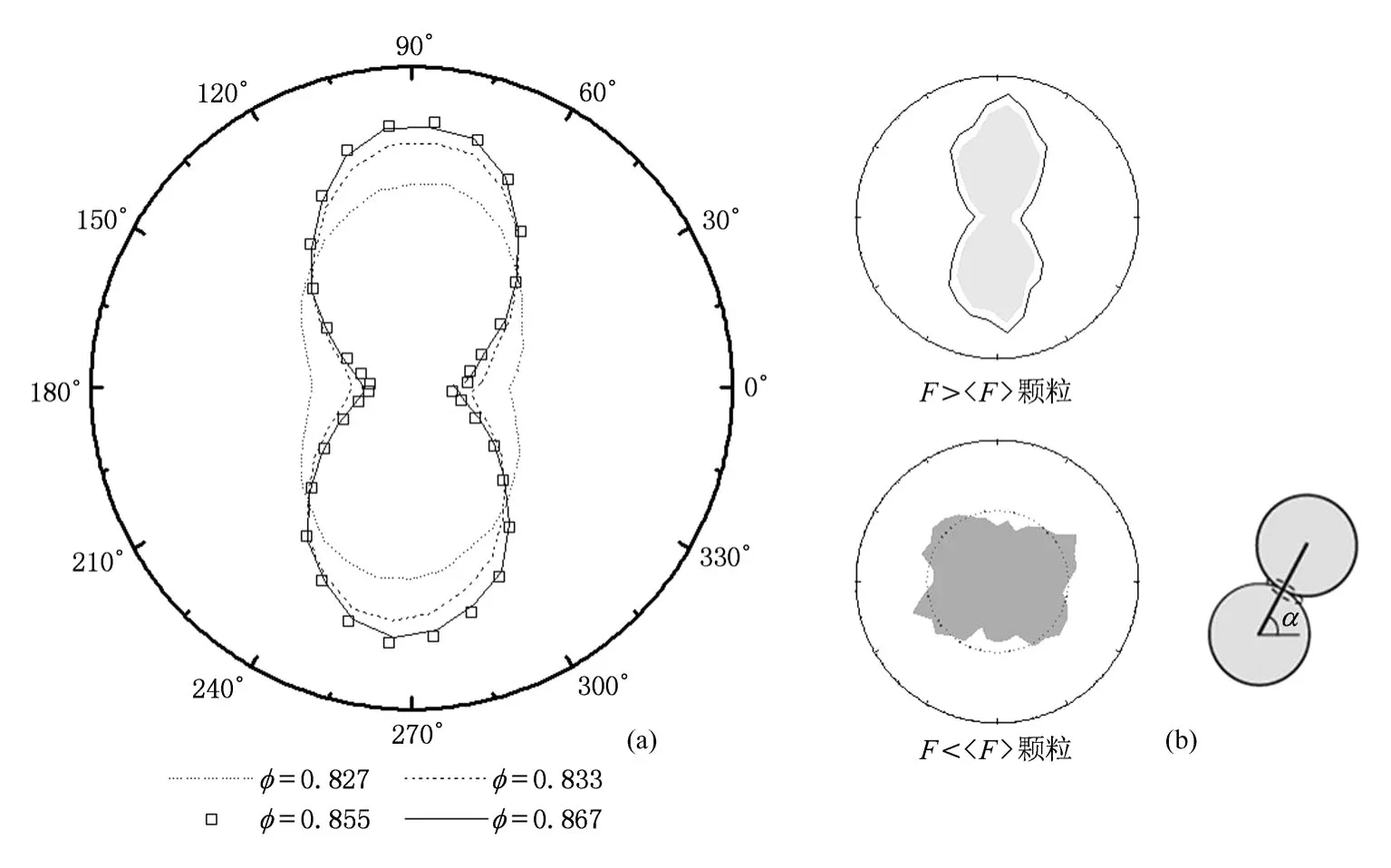
图4 颗粒弹性能的角度分布 (a)不同φ时,F>〈F〉颗粒弹性能量分布;(b)φ=0.848,总弹性能和F>〈F〉颗粒弹性能量分布(F<〈F〉颗粒能量分布放大显示.右下侧是颗粒间接触面角度示意图)
4.力链角度判据
对于静态颗粒体系,人们尝试建立力链网络的理论,比如Bouchaud和Socolar提出了有取向的力链网络概念(directed force chain network),认为力链是若干颗粒组成的线段,每一条线段具有方向和强度,且线段可以连接或断裂.通过类比胶体内微颗粒间的连接结构,固定主轴模型(fixed principal axis model)提出力链至少由3个接触颗粒按线性排列构成,其方向与外荷载的最大主应力方向一致,主要支撑轴向荷载,仅能承受很小的转动或切向滑动,Oda的早期实验工作证实了这一点[1].但是目前还没有被广泛认可的力链定义,对力链还有很多不同的理解.尽管大部分研究者都认为力链具有准直线性和传递较大力(或应力)的特点,但是如何定量的体现力链的准直性(即颗粒质心连线角度变化阈值θc多大(θc见图5(a)所示)仍是一个没有解决的难题.基于第3节的力和能量分析,我们认为用力判断强力链接触力阈值Fc=〈F〉.
θc的确定涉及复杂的机理,需考虑接触面的咬合、内嵌等几何结构特点以及自锁平衡等力学行为.显然,θc的数值对力链长度影响比较大,随着θc的增加,可供寻找的颗粒数目增加,连接成力链的概率增加,特别是长力链的数目和概率会增加.不同的研究者对θc的取值也不同,具有很大的随意性,例如, Peters等[23]取θc为45°,而Pöschel和Schwager[24]取θc为30°,且他们均未对取上述θc取值的理由做进一步说明.我们曾经尝试忽略变形面的咬合和内嵌的等几何行为,仅考虑颗粒表面的自锁机理,而简单取θc=arctan(μs).对于颗粒表面摩擦系数μs=0.3, θc=17°的情况,由于θc取值过小,找到的力链数目较少,不能很好的复现整个力链网络.显然,确定θc值时仅考虑颗粒表面的自锁机理是不太合理的,还应更多的考虑力链网络几何结构特点.我们认为,θc的数值应由其配位数Z的平均值〈Z〉来确定,满足

〈Z〉综合反映了颗粒物性(μs、弹性模量和泊松比等)、级配、颗粒体积份额φ等几何参数和物性参数对颗粒体系几何结构的影响.
图5(b)为我们模拟得到的系统的平均颗粒配位数〈Z〉随体积份额φ的变化曲线.由图5(b)可知, φ=0.848时〈Z〉=4.00,亦即一个颗粒周围约平均有4个颗粒与之发生接触,那么θc=180/〈Z〉=45°; φ=0.827时,〈Z〉=3.487,θc=52°;φ=0.886时,颗粒排布更密集,〈Z〉=4.335,θc=42°.
利用〈Z〉确定θc值后,可以寻找系统中存在的各个力链.如果定义F>〈F〉的接触力链为强力链,可进一步找出系统中的强力链.如图5(a)所示,判断一条强力链的过程如下:设颗粒A为起始颗粒,如果颗粒A,B间作用力大于接触力平均值,则A, B首先连成力链的一段;与颗粒B接触的颗粒有3个,只有C和D处于θc的角度范围之内;若只有B和D间的力大于平均力,则D构成该力链上的第三个颗粒;如果在θc的角度内有多个颗粒大于平均力,则选取角度最小的颗粒;依此类推,可以确定一条完成的力链.图6是寻找到的强力链.颗粒挤压结合成网络(见图5(a)),但是接触网络上传递的荷载相差很大(图6(b)中粗、细线表示当地接触连线力的大小),基于上述的判断准则提取出强力链(见图6(c)),分析这些强力链的结构特点(比如长度分布、相互间交接情况等)就成了需要解决的关键问题之一.

图5 判断力链角度示意图 (a)颗粒间的连接;(b)在本工作中,〈Z〉随φ的分布

图6 颗粒连接网络及提取出的强力链(φ=0.848,〈Z〉=4.00,θc=45°,Fc=〈F〉) (a)颗粒接触网络;(b)接触力大小差异较大,大于〈F〉的接触用粗线表示;(c)依据(2),(3)式提取出的强力链
由图6(b),(c)可以看出,对于φ=0.848,基于θc=45°,Fc=〈F〉提取出的强力链网络是合理的,基本提取出了所有接触力大于〈F〉的接触,没有出现强力链过少而不能复现整体网络结构的情况.
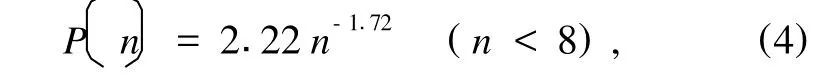
θc越小寻找到的强力链就越接近直线形,我们还尝试计算了θc=30°,35°和40°的情况(见图7).由图7可知,θc的变化对短力链变化不大,说明短力链更接近于直线型;而长力链部分则受θc的变化影响较大,即θc较大时找到的长力链多.但是长力链(比如n>8)仅占总强力链量的10%左右,并且长力链易于断裂,是相对不稳定的.因此,θc从30°到45°范围内,(4)式对于n<8都适用,这说明尽管在压缩过程中局部颗粒间的相对位置和连接都可能发生了变化,但是颗粒间强力链长度的统计性质不变.

图7 强力链长度分布规律
5.侧向压力系数K
径向应力σrr与轴向应力σzz的比值K=σrr/σzz,称为侧压力系数.Janssen假设K为常数来解释粮仓轴向压力按指数规律趋向一饱和值,但是粮仓的K值与颗粒材料性质等有着复杂的关系,一些细节有待进一步的实验测量[25—27].K也是岩土工程分析中的一个基本参数,其具体取值需要进行完整的应力分析计算才能确定.一般认为,K与颗粒材料的内摩擦角直接相关,而颗粒材料的摩擦涉及颗粒的表面滑动摩擦和间嵌入和联锁的咬合摩擦两个本质不同的机理,两者共同概化为内摩擦角:土粒表面越粗糙、棱角越多、φ越大,则颗粒材料的内摩擦角大.从力链角度来看,此时对应的力链结构越稳定,因此颗粒材料的内摩擦角是内部力链结构和强度随外荷载响应的体现,要深入理解内摩擦角和K需从理解力链网络结构入手.
图8是模拟得到的K随φ的变化曲线.由图8可以看出当φ<0.848时,K较大;当φ≥0.848时, K=0.54.一般而言,三维圆柱砂土的侧限试验中K≈0.4—0.5,略小于本文得到的结果.对比图8(b)和(c)颗粒体系内部力链网络情况,φ=0.827时K较大可能与体系不足够密实,力链没有充分发育有关,其方向在统计上按照随机分布.随着上下边壁的挤压,φ增加,体系不断密实,新力链不断生成,且力链的方向逐渐转向σzz方向,分配到侧壁上的份额逐渐较小,当φ≥0.848时K稳定地趋于0.54,此时体系足够密实,力链充分发育,而几乎不再发生变化.
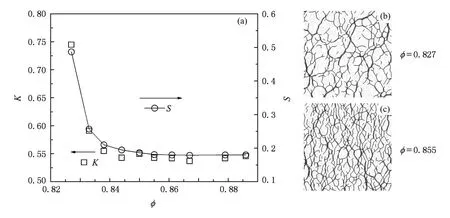
图8 K和S与φ的关系
类比K的定义,我们定义强力链的侧向能量比值S=Wzz/Wrr,其中Wzz和Wrr分别为径向和轴向的弹性能量.根据(1)式可知,当变形极小时,S~F5/3~K5/3,考虑到S的定义很容易得到

模拟计算给出的S随φ的变化关系如图8所示,对比S-φ和K-φ关系,表明强力链的侧向能量比值可能也是由力链的配位数目决定的.K是颗粒体系的
6.结论
1.颗粒体系具有颗粒→力链→体系的多尺度结构,其中颗粒的非连续性和非均匀性是颗粒体系一个基本宏观力学关系,而S是强力链的能量分布,这说明了强力链对颗粒体系宏观力学性质的决定作用.的基本特征,形成复杂接触网络,这为外荷载的传递路径提供了物理基础.但是,力传递路径与接触网络在概念上有本质的不同:力链是力有选择地沿着接触网络传递的路径,接触网络是颗粒排布的几何结构;力链对外荷载加载方式和体系几何特征极其敏感,及时在同一接触网络中随着外荷载加载方式的轻微变化而使得力链形态千差万异;
2.在确定强力链判据后,计算发现强力链和弱力链是性质本质不同的两类力链存在于颗粒体系中.在特定外荷载和几何条件下,强力链发生频繁断裂和重构,决定着颗粒体系应力传播模式、破坏机理好流动本构关系等
3.本文初步揭示了强力链形态力学性质相关,下一步要分析强力链的压缩刚度和弯曲刚度、力链长度、力链交点间距离以及力链半径等,进而形成强力链网络,分析它的力学性能与颗粒体系力学性质的关联,这将是我们下面工作的重点;另外一个分析强力链网络的途径是分析强力接触的单元结构特点(比如采用Laman/Henneberg结构描述),分析单元间的关联进而形成力链网络.
感谢中南大学物理系蒋亦民教授提出了宝贵建议.
[1]Oda M 1972Soils Found.12 17
[2]Matsuoka H 1974Soils Found.14 29
[3]Zhang G,ZhangJ M,Liang D F 2005Chinese J Geotech Eng.27 903(in Chinese)[张 嘎、张建民、梁东方2005岩土工程学报27 903]
[4]Cundall PA,Strack ODL 1979Geotechnique29 47
[5]Oda M,Iwashita K2000Int.J.Eng.Sci.38 1713
[6]Ji S Y,Shen H H 2006Chinese Sci.Bulletin51 646
[7]Luding S,Latzel M,Volk W,Diebels S,Herrmann H J 2001 Comp.Meth.Appl.Mech.Eng.191 21
[8]Dantu P 1957Proceedings of the4th International Conference on Soil Mechanics and Foundation Engineering(London:Butterworth)133 [9]Horne M R 1965Proc R.Soc.London.A 286 62
[10]Edwards S F,Oakeshott R B S 1989PhysicaD 38 88
[11]Bouchaud,J P,Cates M E,Claudin P 1995J.Phys.(France)5 639
[12]Wang WJ,K ong X Z,Zhu ZG2007Phys.Rev.E 75 041302
[13]Sanfratello L,Fukushima E,Behringer R P 2009Granular Matter 11 1
[14]G oldenberg C,G oldhirsch I 2005Nature435 188
[15]Sun Q C,Wang G Q 2009Introduction to The Granular Mantter Mechanics(Beijing:Science Press)(in Chinese)[孙其诚、王光谦2009颗粒物质力学导论(北京:科学出版社)]
[16]Sun Q C,Jin F 2009Wuli(Physics)39 219(in Chinese)[孙其诚、金 峰2009物理39 219]
[17]Sun Q C,Wang GQ,Hu K H 2009Prog.Nat.Sci.,19 523
[18]Landau D,Lifshitz E M 1986Theory of Elasticity(New Y ork: Pergamon)
[19]Johnson K L 1985Contact Mechanics(Cambridge:Cambridge University Press UK)
[20]Albert I,Tegzes P,Kahng B,Albert B R,Sample J G,Pfeifer M, Barabási A L,Vicsek T,Schiffer P 2000Phys.Rev.Lett.84 5122
[21]Stone M B,Barry R,Bernstein D P,Pelc MD,Tsui Y K,Schiffer P 2004Phys.Rev.E 70 041301
[22]Li GX2004Advanced Soli Mechanics(Beijing:Tsinghua University Press)(in Chinese)[李广信2004高等土力学(北京:清华大学出版社)]
[23]Peters J F,Muthuswamy M,Wibowo J,T ordesillas A 2005Phys. Rev.E 72 041307
[24]Pöschel T,Schwager T 2005Computational Granular Dynamics: models and algorithms(Berlin Heidelberg:Springer-Verlag)
[25]Jiang YM,Zheng H P 2008Acta Phys.Sin.57 7360(in Chinese) [蒋亦民、郑鹤鹏2008物理学报57 7360]
[26]Zheng H P,Jiang YM2008Acta Phys.Sin.57 7919(in Chinese) [郑鹤鹏、蒋亦民、2008物理学报57 7919]
[27]Wang H Y,Cao X P,Jiang YM,Liu M2005Acta Phys.Sin.54 2784(in Chinese)[王焕友、曹晓平、蒋亦民、刘佑2005物理学报54 2784]
PACC:0320,4610
Force chains in a uniaxially compressed static granular matter in 2D*
Sun Qi-Cheng1)†Jin Feng1)Wang Guang-Qian1)Zhang Guo-Hua2)
1)(State Key Laboratory of Hydroscience and Engineering,Tsinghua University,Beijing 100084,China)
2)(Department of Physics,University of Science and Technolog Beijing,Beijing 100083,China)
5 April 2009;revised manuscript
22 April 2009)
Granular matter is a large assemblage of dense-packing particles.The interparticle forces are transmitted through heterogeneous chain architecture.The force chains would display different responses as external loading varies,and it would be directly related to the macroscopic mechanical properties of the granular system.Therefore,understanding the properties of force chains is fundamental to the study in granular systems.In this work,we firstly analyzed three characteristic time scales involved in processes occurring in granular systems,and proposed three dimensionless numbers to measure their relative importance. Secondly,a series of numerical simulations were conducted on a uniaxial compression system consisting of 12400 polydispersed particles.Our results showed that the shape of force distributions are unaffected by system preparation history and packing fractions in the range from 0.855 to 0.886,but mainly affected by the static surface friction.By defining three conditions for evaluating strong force chain,the probability distribution of force chain length was found in the form of power law with an exponent of 1.72,which is independent of packing fractions and static surface frictions in this static system.
granular materials,force chain,multi-scale modeling
*国家重点基础研究发展计划(973)项目(批准号:2007CB714101,2010CB731504),清华大学水沙科学与水利水电工程国家重点实验室自主课题项目(批准号:2008-ZY-6)资助的课题.
†E-mail:qcsun@tsinghua.edu.cn
*Project supported by the National KeyBasic Research Programof China(Grant Nos.2007CB714101,2010CB731504)and the Research Fundof the State Key Laboratory of Hydroscience and Engineering(Grant No.2008-ZY-06).
†E-mail:qcsun@tsinghua.edu.cn
