自治广义Birkhoff系统的平衡稳定性＊

张 毅

(苏州科技学院土木工程学院,苏州 215011)

自治广义Birkhoff系统的平衡稳定性＊

张 毅†

(苏州科技学院土木工程学院,苏州 215011)

(2009年3月28日收到;2009年4月19日收到修改稿)

研究广义Birkhoff系统的平衡稳定性问题.建立了自治广义Birkhoff系统的平衡方程;给出了自治广义Birkhoff系统的一次近似方程,利用Lyapunov一次近似理论,建立了系统平衡状态稳定性的判据;构建了Lyapunov函数,利用Lyapunov直接法,建立了自治广义Birkhoff系统平衡状态稳定性的判据.给出了若干算例以说明结果的应用.

广义Birkhoff系统,平衡稳定性,一次近似法,直接法

PACC:0320

1.引言

自Lyapunov创立运动稳定性的一般理论以来,稳定性理论和方法已在自然科学、工程技术等很多学科领域得到了广泛应用,发挥了极其重要的作用[1].梅凤翔[2]全面论述了约束力学系统的稳定性理论,包括完整约束力学系统和非完整约束力学系统的稳定性,以及首先开展了Birkhoff系统的稳定性理论的研究.研究Birkhoff系统稳定性的意义在于:一是Birkhoff系统是Hamilton系统的一个自然推广,其结论不仅适用于Hamilton系统,而且也适用于非经典Hamilton系统;二是Birkhoff系统本身可以当作一类广泛的约束力学系统[3],因此研究Birkhoff系统的稳定性将有助于加深了解约束力学系统的稳定性问题.关于Birkhoff系统的稳定性研究已经取得了一系列重要成果[4-18].本文进一步研究广义Birkhoff系统的平衡稳定性问题,利用Lyapunov一次近似理论和Lyapunov直接法给出了自治广义Birkhoff系统平衡稳定性的一些判据.

2.自治广义Birkhoff系统的平衡方程

自治情形的广义Birkhoff方程可表为

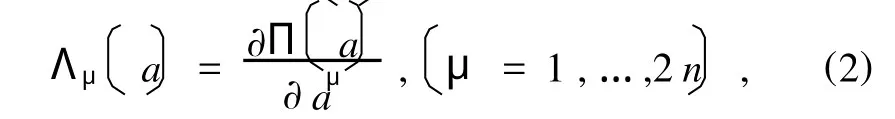
则方程(1)成为

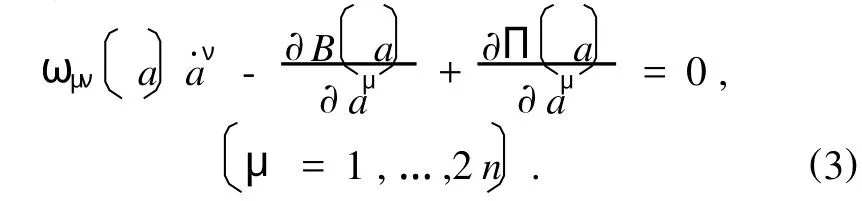
方程(3)可等价地表为

其中

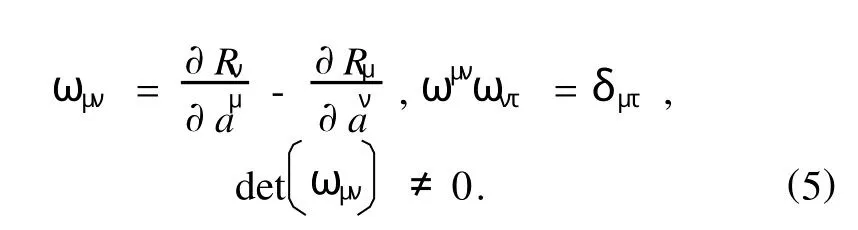
设广义Birkhoff系统(3)的平衡位置为

由于在平衡位置a·μ=0,于是由方程(3)得到平衡方程

这里下标0表示其中的aμ用aμ0替代的结果.如果方程(7)有解,则系统存在平衡位置.如果2n个代数方程(7)是彼此独立的,则平衡位置是孤立的,否则平衡位置组成流形.

3.平衡稳定性的一次近似法

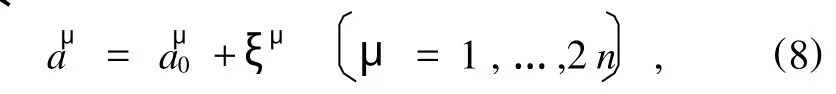
其中ξμ为小量.将(8)式代入方程(3),得

其中未写出之项为ξν,ξ·ν的高阶小项.将(7)式代入(9)式,并忽略高阶小项,便得自治广义Birkhoff系统的一次近似方程

其中

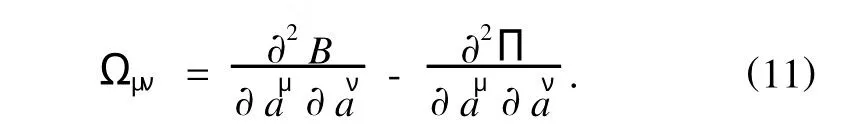
方程(10)的特征方程为

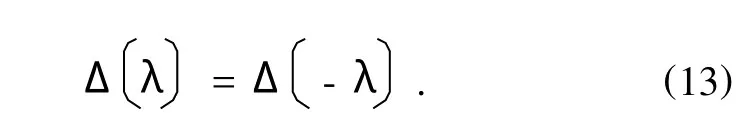
因此,特征方程(12)可写成

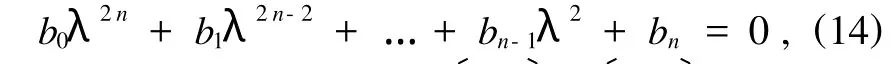
其中系数b0,b1,…,bn可用表出.于是有

命题1 对于自治广义Birkhoff系统(3),其一次近似方程的特征方程(12)的根总是成对互为反号出现的,如有根λ,则必有根

根据Lyapnnov一次近似稳定性理论,有

命题2 对于自治广义Birkhoff系统(3),如果其一次近似方程的特征方程有实部不为零的根,则平衡是不稳定的.

试研究系统的平衡稳定性.

取

则条件(2)满足.广义Birkhoff方程(3)给出

平衡方程(7)给出

由此得到平衡位置

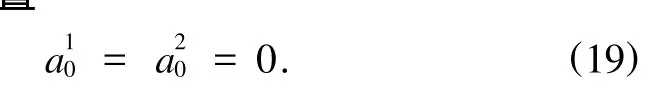
对应平衡位置(19)的一次近似方程为

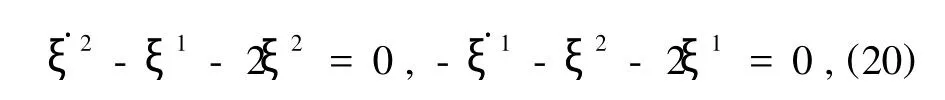
其特征方程为

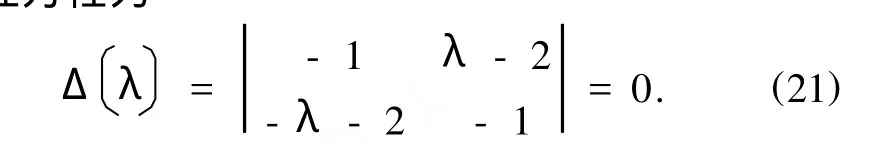
方程(21)有解

由命题2,平衡位置(19)是不稳定的.

4.平衡稳定性的直接法

取Lyapunov函数V为

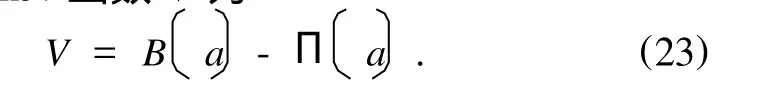
将(8)式代入方程(4),有

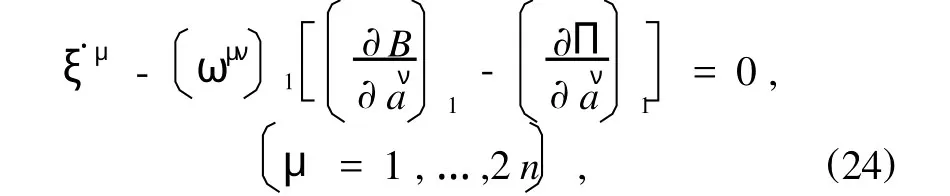
由Lyapunov直接法,得

命题3 对于自治广义Birkhoff系统(4),如果在系统的平衡位置位置附近是定号函数,则系统的平衡位置是稳定的.

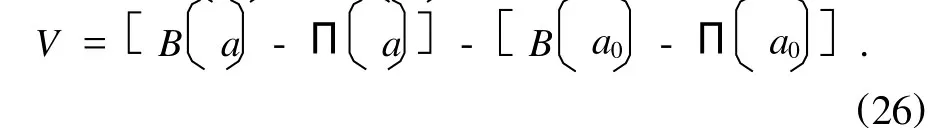
于是命题3成为

置附近是定号函数,则系统的平衡位置是稳定的.

例2 在例1中取附加项为

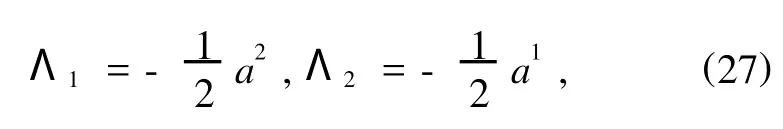
其他条件不变.试研究系统的平衡稳定性.

相应于附加项(27),可取

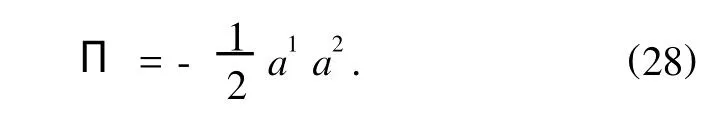
方程(4)给出

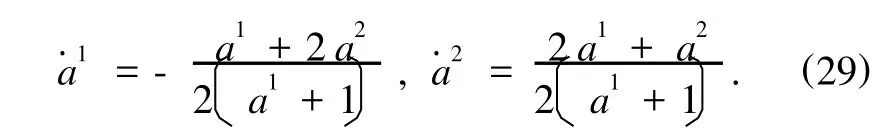
平衡方程(7)给出

于是平衡位置为

取

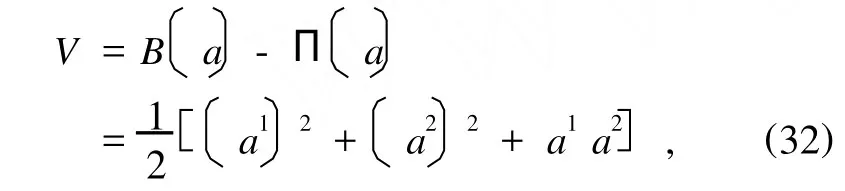
它在平衡位置附件对a1,a2是正定的,按方程(29)求V˙,有

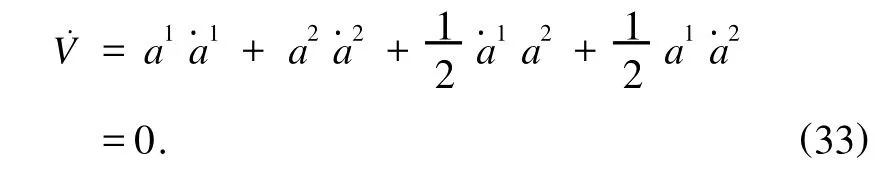
由命题3,平衡位置(31)是稳定的.

5.平衡状态流形的稳定性

以上讨论的前提是假定广义Birkhoff系统的平衡位置是孤立的.下面假设系统的平衡位置不是孤立的,而是组成维数为k的流形ε,有

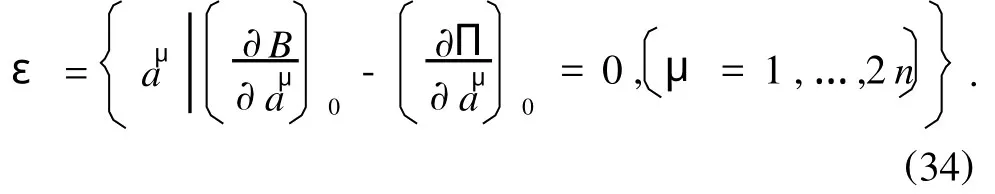
由于假设流形(34)的维数为k,则系统一次近似方程的特征方程(12)至少有k个零根.实际上,由方程(12)得

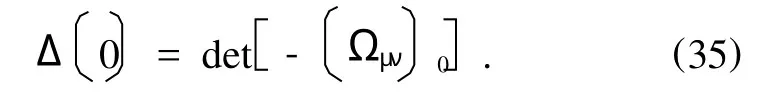
由(11)和(34)式,行列式(35)至少有k行是线性相关的.于是有

命题5 对于自治广义Birkhoff系统(3),如果其平衡状态流形的维数为k,则一次近似方程的特征方程中必有k个零根.在简单地去掉这些零根后,如果剩下的根有实部不为零的根,则平衡状态流形是不稳定的.

由(23)式,(24)式和(25)式,易得

命题6 对于自治广义Birkhoff系统(4),如果函数相对于流形ε是定号的,则系统的平衡状态流形ε是稳定的.

例3 设四阶广义Birkhoff系统的Birkhoff函数和Birkhoff函数组为

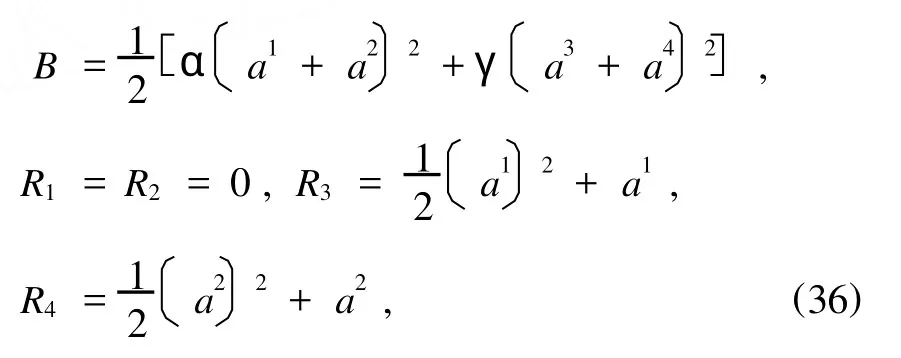
附加项为

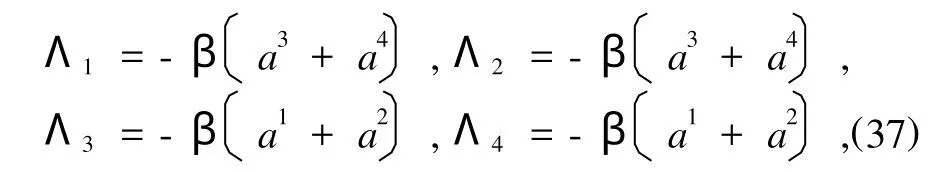
其中α,β,γ为常数,且α γ-β2≠0.试研究系统的平衡稳定性.

取

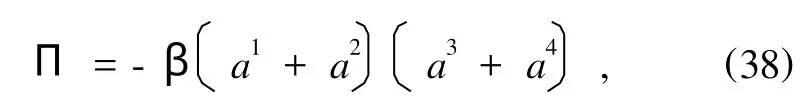
则满足条件(2).平衡方程(7)给出

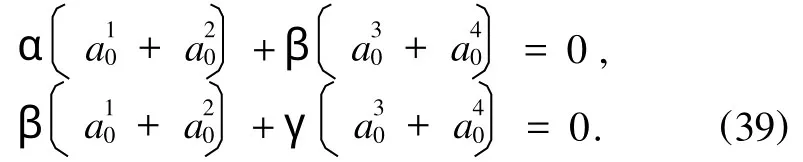
方程(39)有解

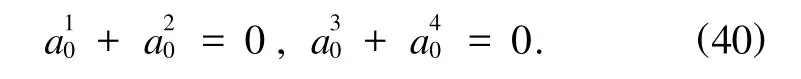
因此系统的平衡位置不是孤立的,而是组成维数为2的平衡状态流形

特征方程(12)给出

即

(43)式有两个零根.简单地去掉零根,有

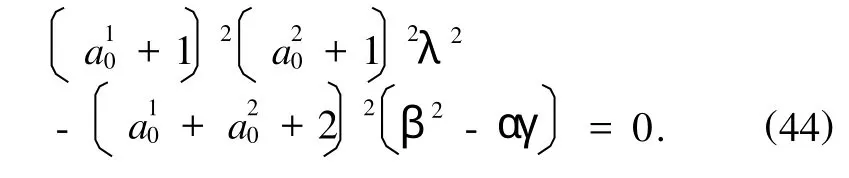
当

时,方程(44)有实部不为零的根,由命题5,平衡状态流形(41)是不稳定的.

取

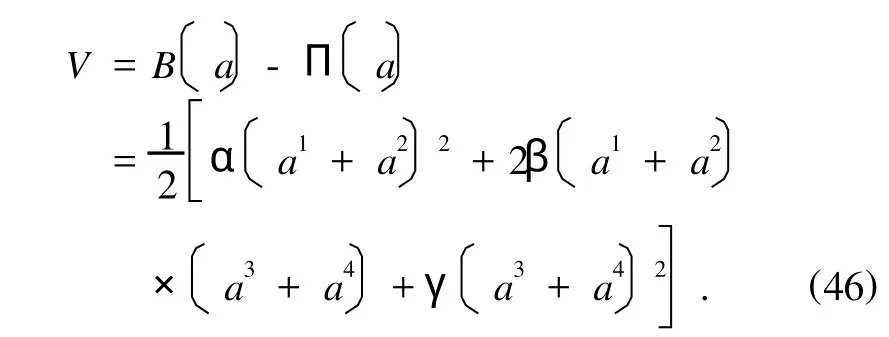
函数V相对流形ε为正定的条件为

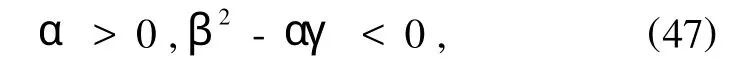
函数V相对流形ε为负定的条件为

由命题6,当满足条件(47)或(48)时,平衡状态流形ε是稳定的.

[1]Wang Z L 1992Stability of Motion and its Applications(Beijing: Higher Education Press)(in Chinese)[王照林1992运动稳定性及其应用(北京:高等教育出版社)]

[2]Mei F X,Shi R C,Zhang YF,Zhu H P 1997Stability of Motion of ConstrainedMechanicalSystems(Beijing:BeijingInstitute of Technology Press)(in Chinese)[梅凤翔、史荣昌、张永发、朱海平1997约束力学系统的运动稳定性(北京:北京理工大学出版社)]

[3]Mei F X,Shi R C,Zhang Y F,Wu H B 1996Dynamics of Birkhoffian System(Beijing:Beijing Institute of Technology Press) (in Chinese)[梅凤翔、史荣昌、张永发、吴惠彬1996 Birkhoff系统动力学(北京:北京理工大学出版社)]

[4]Mei F X 1993Chin.Sci.Bull.38 816

[5]Shi R C,Mei F X,Zhu H P 1994Mech.Res.Commun.21 269

[6]Mei F X 1996J.Beijing Institute ofTechnology16 245(in Chinese)[梅凤翔1996北京理工大学学报16 245]

[7]Mei F X 1997Appl.Math.Mech.18 55(in Chinese)[梅凤翔1997应用数学和力学18 55]

[8]Mei F X 1997J.Beijing Institute of Technology6 106

[9]Xu Z D,Liu E L 1999Appl.Math.Mech.20 531(in Chinese)

[徐振铎、刘尔烈1999应用数学和力学20 531]

[10]Chen X W,Mei F X 2000Mech.Res.Commun.27 365

[11]Chen X W 2002Global Analysis of Birkhoffian System(Henan: Henan University Press)(in Chinese)[陈向炜2002 Birkhoff系统的全局分析(河南:河南大学出版社)]

[12]Fu J L,Chen L Q,Luo Y,Luo S K2003Chin.Phys.12 351

[13]Fu J L,ChenL Q,Xue Y,Luo S K2002Acta Phys.Sin.51 2683 (in Chinese)[傅景礼、陈立群、薛 纭、罗绍凯2002物理学报51 2683]

[14]Fu J L,Chen L Q,Xue Y 2003Acta Phys.Sin.52 256(in Chinese)[傅景礼、陈立群、薛 纭2003物理学报52 256]

[15]Xu Z X2005Acta Phys.Sin.54 4971(in Chinese)[许志新2005物理学报54 4971]

[16]Zhang K,FengJ 2005Acta Phys.Sin.54 2985(in Chinese)[张凯、冯 俊2005物理学报54 2985]

[17]Mei F X,Wu HB,Shang M and Zhang YF 2006Chin.Phys.15 1932

[18]Mei F X,Xie J F,Gang T Q 2007Chin.Phys.Lett.24 1133

[19]Mei F X,Cai J L 2008Acta Phys.Sin.57 4657(in Chinese)[梅凤翔、蔡建乐2008物理学报57 4657]

PACC:0320

Stability of equilibrium for the autonomous generalized Birkhoffian system＊

Zhang Y i†

(College of Civil Engineering,Suzhou University of Science and Technology,Suzhou 215011,China)

28 March 2009;revised manuscript

19 April 2009)

The stability problem of equilibrium for a generalized Birkhoffian system is studied.The equations of equilibrium for the autonomous generalized Birkhoffian system are established.The equations of first approximation of the system are given,and the criterion of stability for equilibrium state of the system is established by using the Liapunov's first approximation theory.The Liapunov'sfunction is constructed,and the criterion of stability for equilibrium state of the system is established by using the Liapunov's direct method.Some examples are given to illustrate the application of the results.

generalized Birkhoffian system,stability of equilibrium,first approximation method,direct method

＊国家自然科学基金(批准号:10972151)和江苏省高校自然科学基金(批准号:08K JB130002)资助的课题.

†E-mail:weidiezh@pub.sz.jsinfo.net

＊Project supported by the National Natural Science Foundation of China(Grant No.10972151)and the Natural Science Foundation of Higher Education Institution of Jiangsu Province,China(Grant No.08K JB130002).

†E-mail:weidiezh@pub.sz.jsinfo.net