各向异性超常材料平板透镜的聚焦特性分析*
2010-09-19刘虹遥罗海陆文双春
刘虹遥 吕 强 罗海陆 文双春
(湖南大学计算机与通信学院微纳光电器件及应用教育部重点实验室,长沙 410082)
各向异性超常材料平板透镜的聚焦特性分析*
刘虹遥 吕 强 罗海陆 文双春†
(湖南大学计算机与通信学院微纳光电器件及应用教育部重点实验室,长沙 410082)
(2009年4月6日收到;2009年5月23日收到修改稿)
运用矢量角谱理论研究各向异性超常材料平板透镜的聚焦特性,得到了光束在平板透镜内外各区域的矢量场分布,揭示了超常材料平板透镜的聚焦特性跟材料的各向异性参数之间的定量关系,发现聚焦场的偏振态因平板透镜的各向异性特性而发生改变.作为矢量理论的具体应用,分析了光轴方向磁导率为-1,其他各向异性参数均为1的超常材料平板透镜的聚焦特性,发现此类透镜对初始沿某一横向方向偏振的光束能实现部分聚焦,并发生偏振旋转现象.
超常材料,平板透镜,部分聚焦,偏振态
PACC:4225B,4230D
1.引言
超常材料平板透镜作为负折射率超常材料最重要的应用之一,近年来成为了研究热点.平板成像首先由Veselago提出,他指出介电常数ε和磁导率μ均为负的材料会发生负折射现象进而实现平板聚焦[1].Pendry进一步指出,满足μ=ε=-1的超常材料平板透镜能够实现“完美成像”:由于近场倏逝波能够在超常材料平板透镜中传输并参与成像,此透镜能够突破传统透镜的衍射极限实现亚波长成像[2].这个开创性的概念引起了人们极大的研究兴趣[3—6].尽管“完美透镜”具有如此诱人的优点,但在实际应用中,各向同性超常材料的制备相当困难,因此许多人将视线投向各向异性超常材料平板透镜[7—15].如,Smith等人用实验和模拟的方式证明了满足z方向磁导率为-1的超常材料平板透镜能够实现近场TE光的部分聚焦[7];Parimi等人提出利用光子晶体中的负折射现象可构造平板透镜[8]; Dumelow等人发现用无磁性各向异性材料同样能构造对TM光有聚焦作用的平板透镜[9].
由于在各向异性超常材料中电磁波波能表现出许多新奇的传输特性[16—22],各向异性超常材料平板能被设计为满足不同需求的光学仪器,如对偏振不敏感的平板透镜[14],偏振分离器[23],滤波器[24,25],等等.研究电磁波通过平板透镜聚焦的问题时,光的偏振态是一个需要考虑的重要问题.然而,目前对此类问题的研究主要基于传统的标量分析法,这种方法将传输的光束看成是标量波的叠加,没有考虑光场的矢量性质,之前的研究大多集中在对聚焦场振幅分布的分析上,忽视了对偏振态的讨论.不同于传统标量分析方法,角谱理论考虑了电磁波的矢量特性,可以描述光束在各个方向上的场分布.基于这个理论,我们能够对各向异性超常材料平板透镜聚焦场的偏振态进行分析.
本文运用角谱理论研究了各向异性超常材料平板透镜聚焦场的偏振特性.从麦克斯韦方程组出发,得到傍轴光束在各向异性超常材料中的矢量传输公式,利用这个公式对各向异性超常材料平板透镜的聚焦场各个方向分量进行了研究.参照Smith等人所制造的材料,选取了一种各向异性超常材料平板透镜进行具体讨论,发现这个透镜实现了初始沿x方向偏振光的部分聚焦,聚焦场的偏振态发生了变化,像平面上y方向场的最大振幅与x方向场的最大振幅在同一个量级.
2.光束在各向异性超常材料中传输的矢量理论
选取光轴为z轴的单轴各向异性超常材料为研究对象,这也是研究各向异性超常材料的一个常用模型[7,16—18].此时,介电张量和磁导率张量可表示为
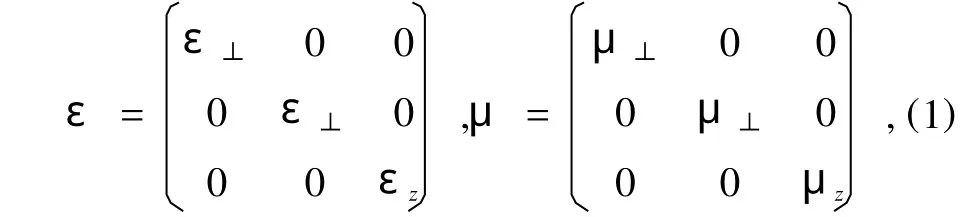
其中εz(μz)和ε⊥(μ⊥)分别表示介电常数和磁导率在平行和垂直于光轴方向上的分量.
考虑一单色电磁波从真空以任意角度入射至各向异性超常材料,其电场E(r,t)=Re[E(r) exp(-iωt)]与磁场H(r,t)=Re[H(r)exp(-iωt)]的复振幅包络满足麦克斯韦方程组:

将(1)式代入(2)式,通过运算,我们得到各向异性超常材料的色散方程:
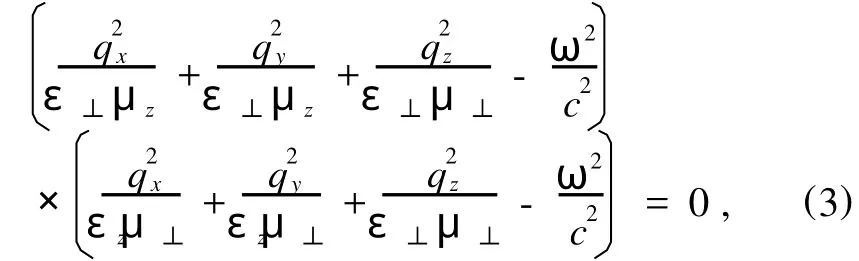
其中qj表示波矢在j(j=x,y,z)方向的分量,ω为电磁波的频率,c表示真空中的光速.假设电磁波沿+z方向传输,由(3)式可知,qz可以取两个不同的值:
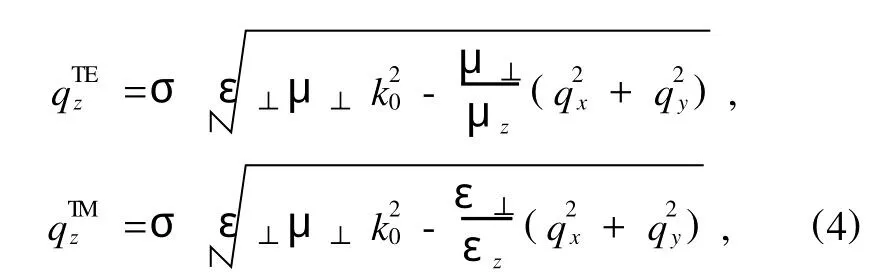
分别对应于TE,TM偏振波[14,21,23].其中,k0=ω/c,表示真空中的波数,σ=±1,我们选择其符号使能流往+z方向流动[13].将(4)式代入(2)式,得到单轴超常材料中正向传输平面波的两组基本解:
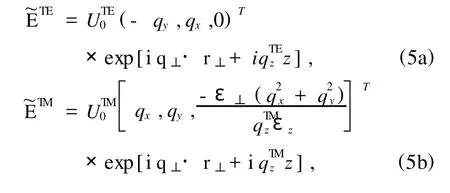
其中UTE0,UTM0为任意常数,q⊥=qxex+qyey,表示波矢q的横向分量.显然,这两组平面波的偏振方向与它的波矢以及材料的各向异性参数有关.
下面利用角谱理论推导光束在各向异性超常材料中的矢量传输公式.由麦克斯韦方程组的线性特征可知,传输光束可以看作平面波的线性叠加.不同于传统的标量研究方法[24],本文将光束处理为两组矢量平面波的线性叠加:
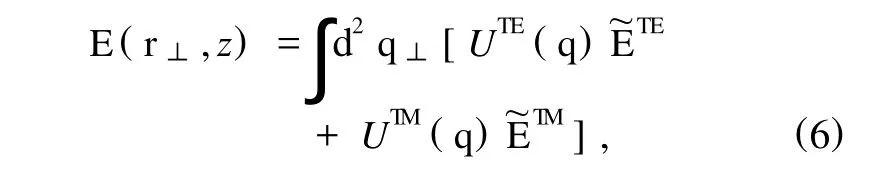
其中UTE(q),UTM(q)决定于入射光束在边界上的分布.显然,(6)式考虑了电场在各个方向的分量,能够用于分析不同位置电场的偏振态.由边界条件可知,边界面处电场和波矢的横向分量相等:
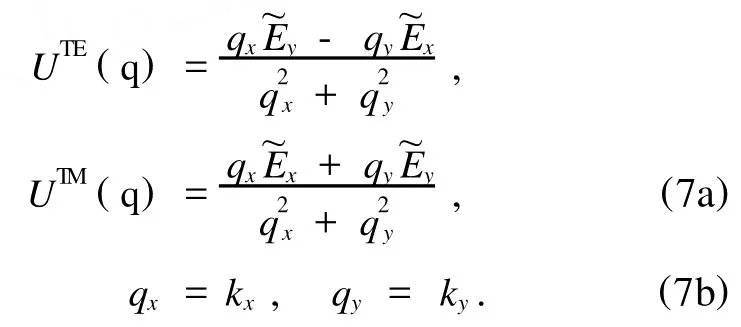
其中~E⊥(k)=~Exex+~Eyey,表示电场在边界处的横向角谱分布,可由对边界电场分布进行傅里叶变换得到
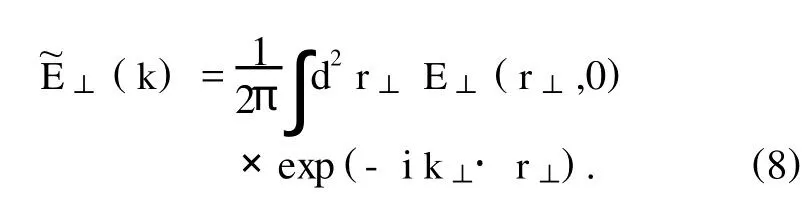
将(5)式和(7)式代入(6)式,得到光束在各向异性超常材料中传输的严格矢量解

(9)式是描述光束传输的一般公式,可以用于研究任意条件下光束在单轴超常材料中的传输问题.下面引入傍轴近似,将qz进行泰勒展开并保留前两项

由(9d)式得到TE波纵向场为零,傍轴条件下波矢分量满足条件此时TM波电场的纵向分量为一阶小量(见(9e)式),因此本文中我们不对纵向场分布进行具体地讨论.将(10)式代入(9)式,得到傍轴光束在单轴超常材料中传输的矢量公式

其中A⊥(r⊥,z)表示横向慢变振幅.为了更加清楚地表现电磁波的折射特性,(11)式中我们引入了TE,TM波的有效折射率nTE,nTM,它们分别满足关系

观察(11)式并与用传统标量方法以及在传统单轴晶体中传输的分析结论进行比较,可以发现许多新奇的现象[19,20,27].首先,由于任意偏振方向的波传输至超常材料中均能产生TE,TM波,光束传输至超常材料中偏振态将会发生改变,这样可能导致平板透镜产生聚焦场的偏振态有所改变.其次,由(11b)和(11c)式可知,超常材料中TE(TM)光束传输过程中是发生会聚的条件为nTE<0(nTM<0),因此有效折射率的定义将超常材料的各向异性参数与光束聚焦特性联系起来.由于TE和TM波的有效折射率决定于不同的各向异性参数,各向异性平板透镜能展现多种不同的聚焦特性.可以根据(12)式选取不同的材料参数,满足各种实际需要.
3.光束通过各向异性超常材料平板的聚焦场分析
如图1所示,将一个各向异性超常材料平板透镜置于真空之中.取物平面为z=0,分界面分别为z =a和z=a+d平面,像平面位于z=a+d+b.考虑一个类高斯入射光束向+z方向传输,初始时沿x轴方向偏振,假设束腰位于物平面,电场分布为

其中,E0为与光强有关的任意常数,w0表示束腰宽度.当入射光束沿任意方向偏振时我们的方法同样适用.

图1 光束通过超常材料平板透镜聚焦示意图(平板透镜位于区域2,两边被真空包围(区域1和3),实线和虚线分别表示物平面和像平面)
将(13)式代入(11)式并取nTE=nTM=1,得到区域1内电场的分布:

取z=a,对(14)式的E1(r⊥,a)进行二维傅里叶变换,将所得到的边界处电场角谱分布代入(11)式,我们得到区域2内的电场分布:
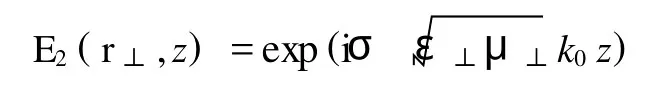
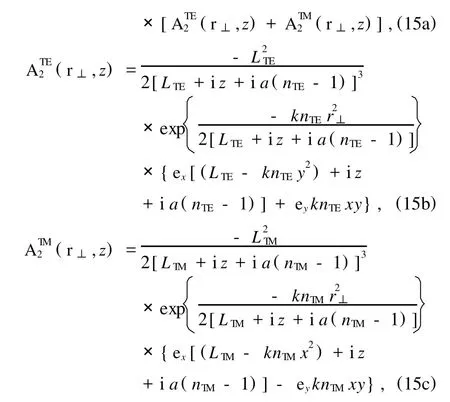
其中LTE=1/2nTEkw20,LTM=1/2nTMkw20,分别表示区域2内TE波和TM波的瑞利距离.为简单起见,在上式推导中假设边界面处电场完美匹配,没有发生反射.
观察(15)式,可以发现一个有趣的现象:光束传输至透镜中偏振态立刻发生了改变.初始沿x方向偏振的光束在第一分界面(z=a平面)处分裂成TE,TM两个光束,它们在y方向上电场振幅分布相同,相位相差π,满足电场连续的边界条件.然而,这两个光束在透镜中独立传输,并且均不再为线偏振光,其偏振态与具体位置以及有效折射率有关.对于TE光,x方向场分量比y方向场分量相位滞后θTE= arctan[(z+anTE-a)/(knTEy2-LTE)].对于TM光, x方向场分量比y方向场分量相位滞后θTM=π/2+ arctan[(z+anTE-a)/(knTEy2-LTE)].
为了进一步研究透镜内的场分布,我们选择一种各向异性超常材料平板透镜为例进行具体分析.根据Smith等人所制造的各向异性超常材料(见文献[11]),取ε⊥=εz=μ⊥=1,μz=-1,a=2 cm,d =4 cm,假设zR=1 cm,w0=1 cm.此时,有效折射率为nTE=-1,nTM=1.图2、图3分别描绘了TE, TM光束在透镜中不同位置处的场振幅分布.在第一分界面处TE,TM光束电场分布相似(见图2(a),图3(a)),然而由于对应的有效折射率符号相反,它们在透镜中表现出不同的传输性质.TE光束具有负的瑞利距离[3],在区域2内发生会聚,两个边界面处电场分布相同(见图2).TM光束则具有正瑞利距离,在传输不断发散,束腰宽度不断的增加(见图3).

图2 透镜内TE光束电场的振幅分布图(第一、二列分别表示x,y方向电场的分布;从图上可以发现TE光束在区域2发生会聚,第一、二边界面处电场分布相同) (a)第一边界面;(b)透镜内的像平面;(c)第二边界面
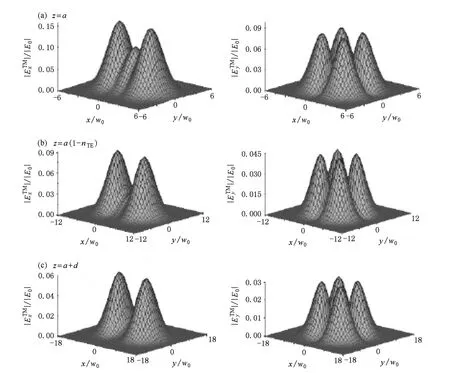
图3 透镜内TM光束电场的振幅分布图(第一、二列分别表示x,y方向电场的分布;显然TM光束在区域2传输时继续发散,光束不断展宽) (a)第一边界面;(b)透镜内TE光束的像平面;(c)第二边界面
图4描绘了透镜内TE(a),TM(b)光束束宽随距离变化图.η方向光束束腰宽度定义为[28]
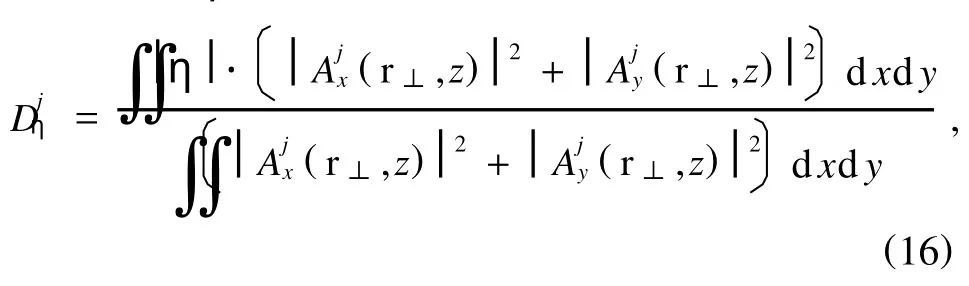
其中j=TE,TM,η=x,y.显然,透镜内TE光束以会聚的方式传输,TM光束以发散的方式传输.由于超常材料的各向异性特性,平板透镜内光束不再为圆对称分布.尽管变化趋势相一致,平板透镜内光束在x方向与y方向的束腰宽度相差较大,这在图2,图3中同样能得到体现.
现在我们开始分析区域3的电场分布.取(15)式中z=a+d并进行傅里叶变换,将得到的第二边界面处的角谱分布代入(11)式.使nTE=nTM=1,得到区域3内的电场分布

其中A31(r⊥,z),A32(r⊥,z)分别表示区域2内的TE光束和TM光束传输至区域3产生场的慢变振幅.显然,区域3内y方向的场分量不为零,并且光束不再为线偏振光.电场由两部分线性叠加而成,这两部分为别由区域2内的TE,TM光束通过第二边界面产生.由于区域2内TE,TM光束独立传输,有效折射率决定于不同的各向异性参数,各向异性超常材料平板透镜能够表现出不同的聚焦特性.nTE· nTM<0时,透镜实现了光束的部分聚焦;nTE<0且nTM<0时,透镜能实现光束的完全聚焦;nTE>0且nTM>0时,光束不能聚焦.注意平板透镜的厚度必须满足条件d>-an(其中,n=min(nTE,nTM)且n <0),否则光束在透镜以及区域3内无法聚焦.此时,像平面的位置为b=-d/n-a.
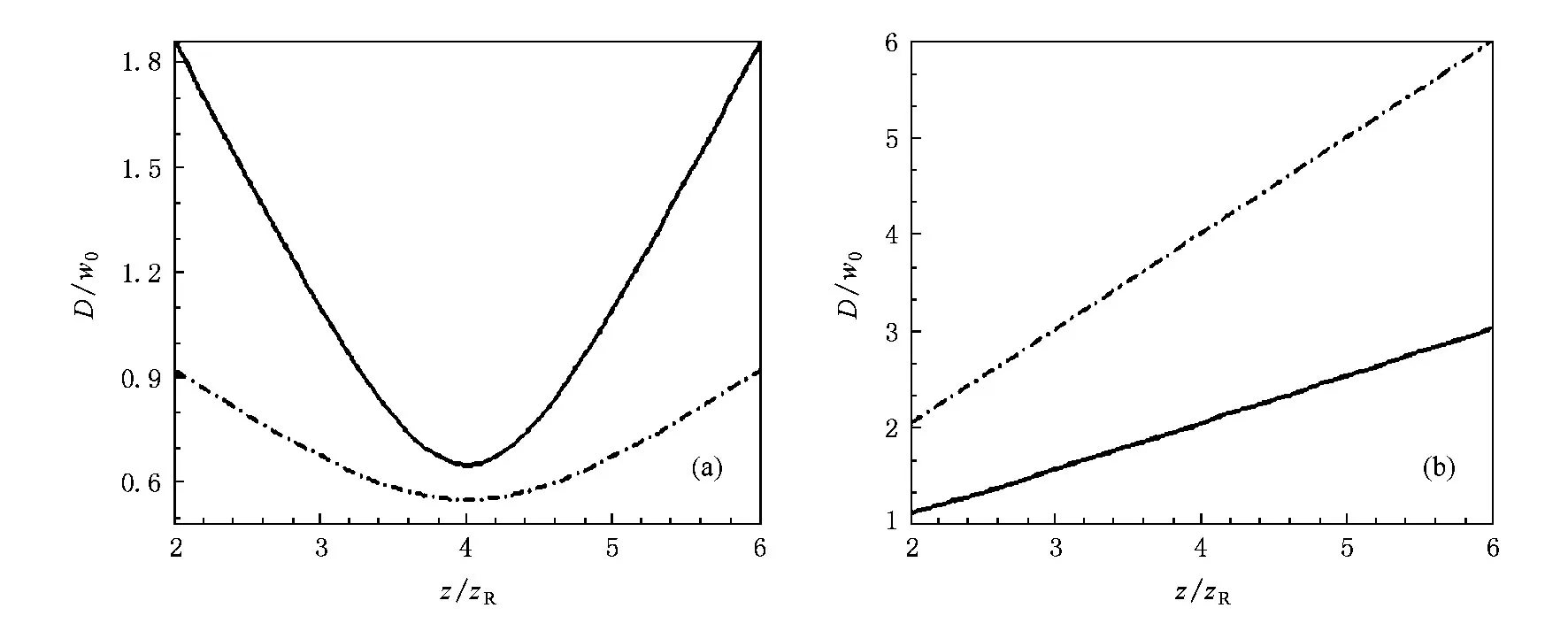
图4 透镜内TE(a),TM(b)光束束宽随距离变化图(图中虚线表示x方向束宽,实线表示y方向束宽.显然TE,TM光束在平板透镜内分别以会聚、发散的方式传输)
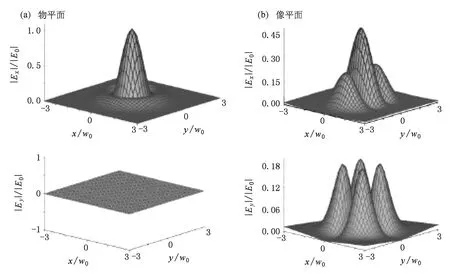
图5 光束在物平面(a)以及像平面(b)的电场振幅分布图(第一、二行分别表示x,y方向的电场分布.从图中可以看出,像平面电场的偏振态发生改变,y方向的电场不为零)
下面我们以Smith等制造的各向异性超常材料平板透镜为例进行具体分析,此时像平面的位置为b=2 cm.与Smith等人的结论一致,我们发现此透镜实现了光束的部分聚焦:区域2的TE光束传输至区域3在像平面上发生聚焦,而区域2的TM光束一直发散传输,它在区域3所产生的场分布范围广、振幅小,相对于区域2内TE光束产生的场可以忽略,在实验中也很难检测到.因此,像平面上x方向的电场失去了圆对称性,振幅约减少为物平面电场振幅的一半.注意物平面光束沿任意方向偏振时,均会发生部分聚焦.综合上面的分析,我们揭示了部分聚焦的物理本质:入射光束由物平面向正方向传输,当它传输至平板透镜时,由于透镜的各向异性特性,传输光束可看成两个独立传输的矢量光束(TE,TM光束)的线性叠加.其中,TE光束在透镜中以聚焦的方式传输,并在区域3内成像.另一方面,TM光束在透镜里传输时不断地发散,不能在区域3内成像.因此部分聚焦就是区域2中的TE光束部分发生聚焦.
图5描绘了物平面、像平面上电场的振幅分布.与物平面相比较,像平面上电场的偏振态发生了改变.像平面y方向的场分布不为零,它的最大振幅与x方向场的最大振幅在同一个量级.偏振改变现象源于电场的部分聚焦:初始沿x方向偏振的光束在透镜中分裂成TE,TM光束的线性叠加,在第一个边界面处,TE,TM光束y方向场振幅分布相同,相位相差π,叠加后可以抵消.然而由于电场发生部分聚焦,透镜中TE,TM光束表现出不同的传输特性,在像平面上TE,TM光的y方向场不再能相互抵消, TM光y方向场分布范围广,振幅小,在靠近光轴处可忽略.这个现象在Smith等人的实验中应该同样会出现.由于像平面上y方向场分布较明显,这个现象在各向异性平板透镜成像的实验中应该引起注意.
4.结论
利用角谱理论研究了单轴各向异性超常材料平板透镜的聚焦特性,得到光束在各个区域的矢量场分布.通过对平板透镜中TE和TM光束有效折射率的定义,发现各向异性参数不同的超常材料平板透镜能表现出不同的聚焦特性.与入射光束相比较,聚焦场的偏振态发生了改变.作为应用,参照Smith等人所制作的材料选取一种超常材料平板透镜进行了具体分析,我们发现此透镜对初始沿x方向偏振的光束同样实现了部分聚焦:入射光束传输至平板透镜时分裂成TE和TM两个独立传输光束,其中TE光束在透镜中以会聚的方式传输并在像平面成像,而TM光束则在传输中不断地发散,不能成像.对像平面上各个方向电场分布的考察发现,像平面y方向的电场不为零,它的最大振幅与x方向电场的最大振幅在同一个量级,这种偏振旋转现象是由光束发生部分聚焦产生的,不能用传统的标量理论得到.
[1]Veselago V G1968Sov.Phys.Usp.10 509
[2]PendryJ B 2000Phys.Rev.Lett.85 3966
[3]Luo HL,Hu W,Ren Z Z,Shu W X,Li F 2006Opt.Commun.266 327
[4]Luo HL,Ren Z Z,Shu W X,Wen S C 2008Phys.Rev.A 77 023812
[5]Dong Z G,Zhu S N,Liu H 2006Chin.Phys.15 1772
[6]Lin ZL,DingJ C,Zhang P 2008Chin.Phys.B 17 954
[7]Smith D R,Schurig D,Mock J J,K olinko P,Rye P 2004Appl. Phys.Lett.84 2244
[8]Parimi P V,Lu W T,Vodo P,Sridhar S 2003Nature426 404
[9]Dumelow T,Costa J A P,Freire V N 2005Phys.Rev.B 72 235115
[10]Parazzoli C G,Greegor R B,Nielsen J A,Thompson M A,Li K, Vetter A M,Tanielian M H 2004Appl.Phys.Lett.90 3232
[11]Shen N H,Wang Q,ChenJ,Fan YX,DingJ P,Wang H T,Tian Y J,Ming N B 2005Phys.Rev.B 72 153104
[12]Elser J,Wangberg R,Podolskiy V A 2006Appl.Phys.Lett.89 261102
[13]Smith D R,Schurig D 2003Phys.Rev.Lett.90 077405
[14]Luo HL,Ren Z Z,Shu W X,Li F 2007Phys.Rev.E 75 026601
[15]Lu W T,Sridhar S 2008Phys.Rev.B 77 233101
[16]Lindell I V,Tretyakov SA,Nikoskinen KI,Llvonen S2001Microw. Opt.Tech.Lett.31 129
[17]Hu L B,Chui S T 2002Phys.Rev.B 66 085108
[18]Shelby R,Smith D R,Nasser N,Schultz S 2001Appl.Phys.Lett. 78 489
[19]Luo HL,Hu W,Y i X N,Zhu J 2004Acta Phys.Sin.53 2947(in Chinese)[罗海陆、胡 巍、易煦农、朱 静2004物理学报53 2947]
[20]Cao J X,Hu W,Luo HL,Yang XB 2007Acta Phys.Sin.56 2131 (in Chinese)[曹京晓、胡 巍、罗海陆、杨湘波2007物理学报56 2131]
[21]Luo HL,Ren Z Z,Shu W X,Li F 2007Appl.Phys.A 87 245
[22]Zhou J H,Liu H Y,Luo H L,Wen S C 2008Acta Phys.Sin.57 7729(in Chinese)[周建华、刘虹遥、罗海陆、文双春2008物理学报57 7729]
[23]Luo HL,Ren Z Z,Shu W X,Li F 2007Appl.Phys.B 87 283
[24]Xiang YJ,Dai X Y,Wen S C,Fan D Y2008Opt.Lett.33 1255
[25]ZhouJ H,Luo H L,Wen S C,Fang A L,Zhuang B X 2009Acta Phys.Sin.58 1765(in Chinese)[周建华、罗海陆、文双春、方安乐、庄彬先2009物理学报58 1765]
[26]Lax M,Louisell W H,McKnight W B 1974Phys.Rev.A 11 1365
[27]Born M,Wolf E 1999Principles of Optics(Oxford:Cambridge University Press)
[28]Cincotti G,Ciattoni A,Palma C 2001IEEE J.Quantum Electron. 37 1517
PACC:4225B,4230D
Focusing properties of the uniaxially anisotropic metamaterial slab lens*
Liu Hong-Yao LüQiang Luo Hai-Lu Wen Shuang-Chun†
(Key Laboratory for Micro/Nano Optoelectronic Devices of Ministry of Education,
School of Computer and Communication,Hunan University,Changsha 410082,China)
6 April 2009;revised manuscript
23 May 2009)
We studied the focusing properties of an anisotropic metamaterial slab lens by means of the angular spectrum representation of the vectorial electromagnetic field.The analytical expressions for vectorial fields in all the propagation regions are obtained, and the quantitative relationship between the focusing characteristics of the vectorial electromagnetic field and the anisotropic parametersof the anisotropic metamaterial slab lens is disclosed.The polarization state of the focusing beam is found to be changed due to the effect of anisotropy.As an application of the vectorial theory,we have analyzed the focusing property of an anisotropic metamaterial slab for which the permeability along longitudinal axis is-1.It is demonstrated that this slab lens can redirect a beam initially polarized along a transverse axis to a partial focus and give a clear polarization rotation of the beam.
metamaterial,slab lens,partial focusing,polarization state
*国家自然科学基金(批准号:10974049,10804029)和国家博士后科学基金(批准号:20080431018)资助的课题.
†E-mail:scwen@hnu.cn
*Project supported by the National Natural Science Foundation of China(Grant Nos.10974049 and 10804029)and National Science Foundation for Postdoctoral Scientists(Grant Nos.20080431018).
†E-mail:scwen@hnu.cn
