一种步长为对角阵的正交数据投影算法

郭艺夺,张永顺,童宁宁,沈 堤

(空军工程大学导弹学院,陕西 三原 713800)

0 引言

基于特征子空间的算法的共同特点是需进行特征分解,但特征分解的运算量大,算法复杂,工程实现较难。此外,这些特征分解及特征子空间方法是一类批处理方法,即在获得所有观测数据后进行一次性处理。显然,这种处理方法只适于参数或统计特性不随时间变化的系统和信号,而不适于参数或统计特性时变的系统和信号。对此,研究者提出用子空间迭代和更新算法改进特征子空间算法。YANG于1995年提出的映射逼近子空间算法是应用较广的一种估计信号子空间的快速算法,该算法的本质是无约束最优化,其结构简单,只需迭代更新1个参数,缺点是不能提供正交估计[1]。文献[2、3]分别提出了改进的正交化算法,虽可获得正交的信号子空间基的估计,但算法结构复杂,运算量有所增加,需实时更新4个参数。文献[4]提出了一种跟踪噪声子空间的FRANS算法,对数据映射方法采用快速正交化措施,但该种正交化处理并不稳定且出现发散。

基于数据投影算法,本文提出了一种步长为对角阵的正交DPM算法。

1 信号及噪声子空间的正交迭代

文献[5]证明,在平稳状况下所希望的静态权重可通过极小化(对应噪声子空间估计)或极大化(对应信号子空间估计)线性组合器输出的均方值(代价函数)Ψ求得,即

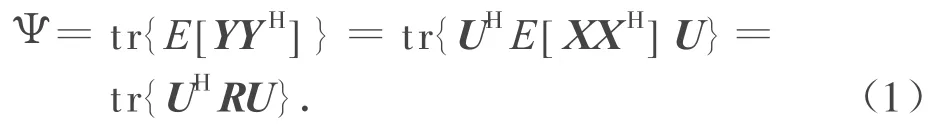
式中：E为数学期望;Y,X分别为线性组合器的输出和输入矢量;R为输入矢量的协方差阵;U为N×m阶加权阵,服从正交化约束条件

此处：Im为单位阵;上标H表示共轭转置。显然,若信源数为L,对信号子空间的估计可选择m=L,而对噪声子空间的估计,则选择m=N-L。

因式(1)的代价函数Ψ是一约束极值化问题,显然可用梯度法(GET)实现,即权矩阵的更新为

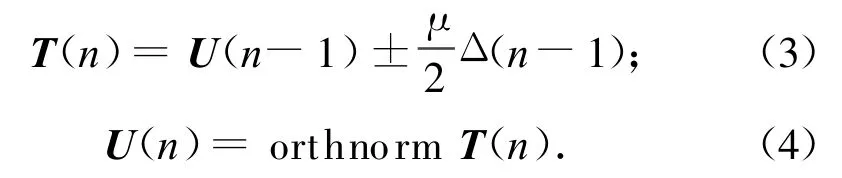
式中：T(n)为第n次迭代时GET法获得的加权矩阵的估值;μ为收敛速率;n=1,2,…;Δ(n)为Ψ相对U(n)的梯度估计子,且

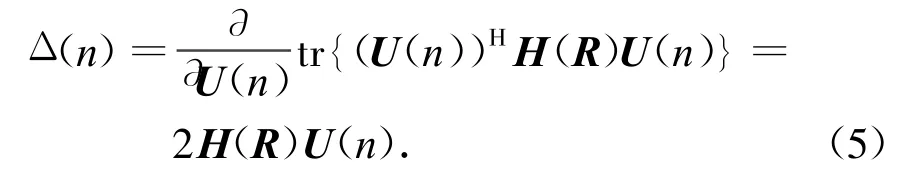
则式(3)、(4)可写成

式中：Q(R)=I±μR。则可得

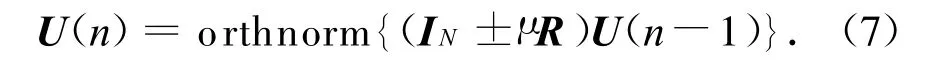
因R的特征值为减函数,式(7)中取“+”时为最大化问题,为估计信号子空间;取“-”时,为最小化问题,即为估计噪声子空间。

当数据的R无法一次性获得,而只能获得连续的数据矢量序列{x(n)}时,可用一自适应估计R(n)替代式(7)中的R,且R(n)满足E[R(n)]=R。则自适应的正交迭代算法可表示为

显然,求解R(n)最简形式是对数据协方差矩阵的即时估计方法,即R(n)=x(n)(x(n))H。此处：x(n)为时刻n的数据矢量。则式(8)可表示为

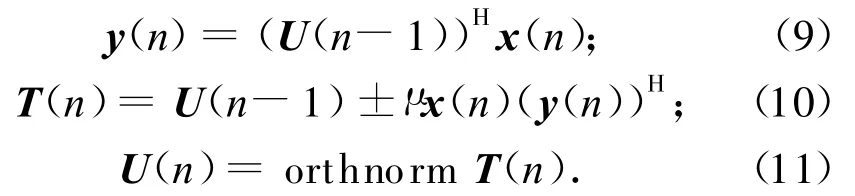
式(9)～(11)即为常规DPM[5]。

2 步长为对角阵的正交DPM

观察DPM可发现：该算法每次迭代对T(n)的每列都使用相同步长μ。可预见,若每次迭代对T(n)的每列使用不同步长,则DPM的性能将会有进一步提高,因为子空间每列可有不同的动态收敛速度。因此,本文在DMP算法的基础上,每次迭代时对T(n)的每列应用不同的步长,并对所得每列进行正交归一化处理以使获得的U(n)为标准正交阵。

2.1 算法描述

记第n次迭代中每列使用的步长为μr(n)(r=1,…,m),则可得

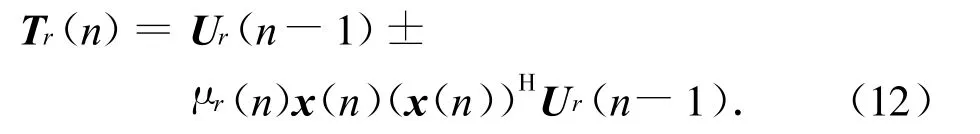
为使U(n)为标准正交矩阵,在每次迭代提取第r个特征向量Tr(n)时,将其与前r-1个已得的特征向量作单位正交化处理,以保证已估得的r个特征向量均正交。同样如此提取第r+1个特征向量,依此类推,直至所有特征向量都提取完。这样,在每次迭代提取任一特征向量时都保证此特征向量与之前估计的特征向量正交,从而保证所有特征向量相互正交。设

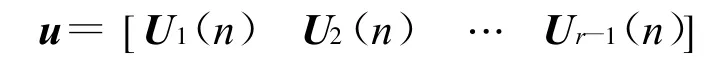
为第n次迭代时r-1个已得的单位正交特征向量;Wr(n)为第n次迭代时第r个正交特征向量;Ur(n)为第n次迭代时第r个单位正交特征向量,则在第n次迭代时第r个特征向量时的单位正交化模型为

需指出,当r=1时,U1(n)可直接对T1(n)进行单位化,即

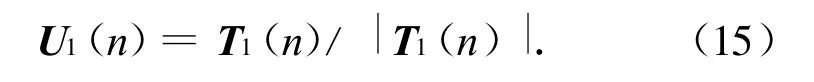
2.2 最优对角阵步长求取

由前文可知,DPM算法在第n次快拍的代价函数

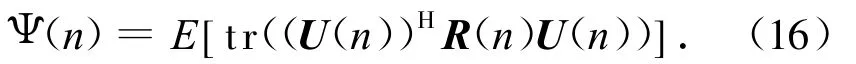
若忽略正交单位化这一个步骤,式(16)可用E[tr((T(n))HR(n)T(n))]近似表示。将T(n)代入其中,可得

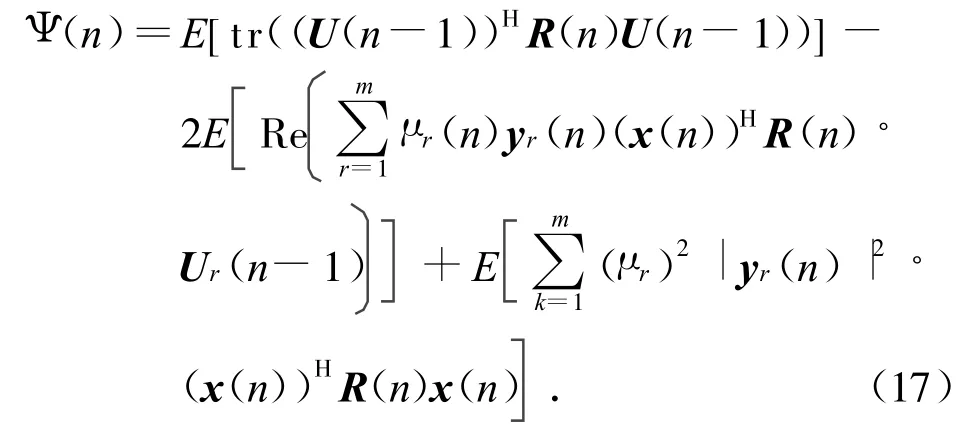
式中：yr(n)为y(n)的第r个元素,且yr(n)=(Ur(n-1))Hx(n)。

为求得最优的步长因子μr(n),用式(17)对μr(n)求偏导,并令该偏导为0,即

式中：r=1,…,m。求解式(18)可得

假设Ur(n-1),x(n)相互独立,则可得μr(n)的估值

式中：γ,σ为可提高算法稳定性的正常数,0＜γ＜1;

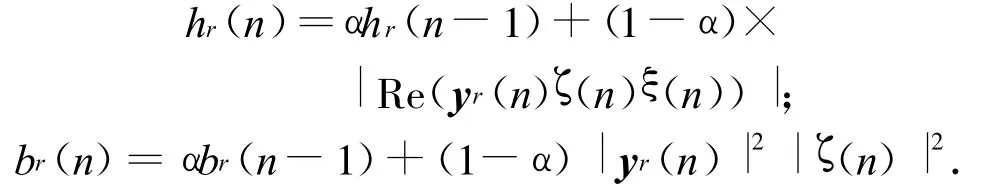
此处：α为遗忘因子,且0＜α＜1;

3 仿真

因估计信号子空间的算法的性能与估计噪声子空间的算法性能基本相同,仿真中只对估计噪声子空间的算法进行分析。仿真中,取α=0.998,γ=0.12,σ=0。

3.1 算法跟踪性能分析

迭代初始值U(0)取为L×L单位矩阵的前m列,阵元数为10。本文用MUSIC算法估计信号源的到达方向(DOA)[7]。

仿真1(算法对机动目标的跟踪性能)：采用100次观察,3个独立信号源,方位分别为30°,-20°,-60°,其中30°信号源在前50个快拍按-0.2°/每次快拍数变化,后50个快拍信号的方位变为45°,并按0.3°/每次快拍数变化;-20°信号源为一固定信号源;-60°信号源按0.2°/每次快拍数变化。仿真结果如图1所示。图中：θ为目标的方位角。

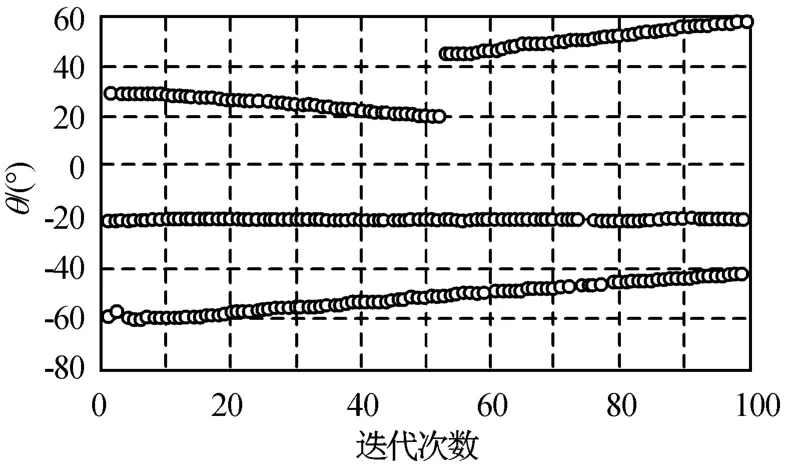
图1 对机动目标的跟踪性能Fig.1 Tracking performance of mobiletarget

仿真2(算法对角度交叉目标跟踪性能)：采用200次观察,2个独立信号源,方位分别为30°,-30°,其中-30°信号源按0.3°/每次快拍数变化,30°信号源按-0.3°/每次快拍数变化。仿真结果如图2所示。

图2 对角度交叉目标的跟踪性能Fig.2 Tracking perf ormance of crossing targets

由图1、2可知：本文的步长为对角阵的正交DPM算法均以较高的精度和稳定性跟踪各种目标,说明本文算法有效。

3.2 算法统计性能分析

仿真中,取数据协方差阵

其中：L=4,m=2。R的特征值为0.015 7,0.169 0,0.605 8,2.309 6。为描述算法的统计性能,定义反映算法统计性能的平均性能因子为

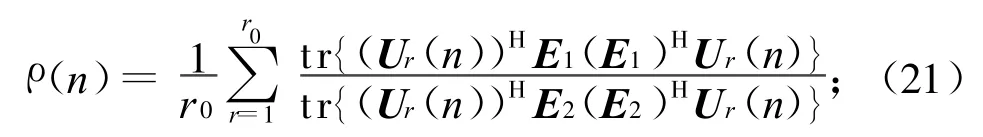
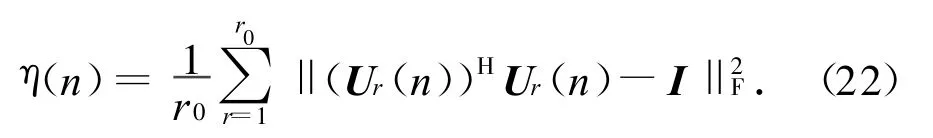
式中：r为每次快拍算法运行的次数,仿真中r0=50;表示取Frobenius范数;E1,E2分别表示实际的信号和噪声子空间[8]。ρ(n)表征噪声子空间的估计精度,若欲衡量信号子空间的估计精度,则只需将ρ(n)中的E1,E2互换即可。η(n)表示估计噪声子空间的正交性误差。初始值U(0)选为矩阵IL的前2列,约束条件为(U(0))HU(0)=IM。

文献[4]FRANS算法、文献[9]FDPM算法与本文算法的比较分别如图3、4所示。仿真中仅取H(R)=R估计噪声子空间的这种算法。其中,FRANS,FDPM算法中μ=0.02。

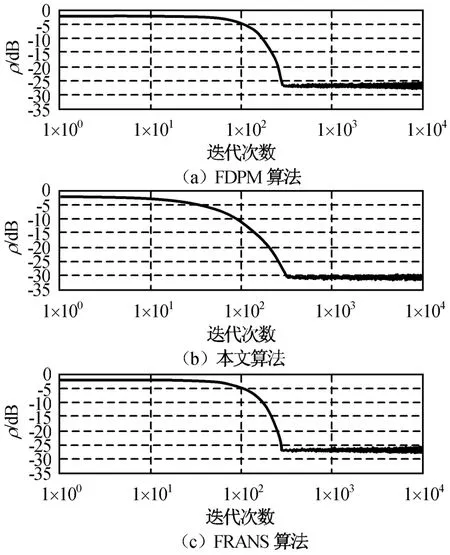
图3 不同算法的跟踪精度Fig.3 Tracking precision of various algorithms

由图3可知：FRANS,FDPM两种算法的跟踪精度曲线基本重合,其跟踪性能基本相同,但与本文算法相比,其跟踪精度较差,这是因为本文算法的每次迭代对U(n)的每列应用的步长不同,提高了性能。由图4可知：FDPM算法和本文算法是稳定的,FRANS算法正交性误差随迭代次数的增加而迅速增大,但本文算法噪声子空间估计的正交误差小于FDPM算法。

图4 不同算法的正交性误差Fig.4 Orthonormal error of various algorithm

4 结束语

本文在常规的DPM算法的基础上,提出一种步长为对角阵的正交DPM算法。该算法每次迭代时对估计的子空间的每列应用不同的步长,并对所得的每列作正交归一化处理,由此保证估计的子空间为标准正交,运行时不存在累积性误差;又因采用“自适应”而非固定步长,能更好地匹配子空间的动态收敛速度。因此,相对其他算法(如FRANS,FDPM算法)来说,该算法的跟踪性能更优。仿真结果验证了算法的有效性。

[1]YANG B.Projection approximation subspace tracking[J].IEEE Transaction Signal Process,1995,43(1)：95-107.

[2]CHONAVEL T,CHAMPAGNEB,RIOU C.Fast adaptive eigenvaluede composition：A maximum likelihood approach[J].Signal Process,2003,51(4)：307-324.

[3]CHAMPAGNE B,LIU Q G.Plane rotation-based EVD updating schemes for efficient subspace tracking[J].IEEE Transaction Signal Process,1998,46(7)：1886-1900.

[4]ATTALAH S.The generalized Rayleigh's quotient adaptive noise subspace algorithm：A householder transformation-based implementation[J].IEEE Transaction Circuits System II,2006,53(1)：3-7.

[5]YANG J F,KAVEH M.Adaptive eigensubspace algorithms for direction or frequency estimation and tracking[J].IEEE Transaction on ASSP,1988,36(2)：241-251.

[6]HAYKIN S.Adaptivefilter theory[M].Upper Saddle River：Prentice Hall,2002.

[7]SCHMIDT RO.M ultiple emitter location and signal parameter estimations[J].IEEE Transaction Antennas and Propagation,1986,34(3)：276-280.

[8]ABED-MERAIM K,ATTALAH S,CHKEIF A,et al.Orthogonal OJA algorithm[J].IEEE Signal Process.Letters,2000,7(5)：116-119.

[9]DOUKOPOULOS X G,MOUSTAKIDES G V.The fast data projection method for stable subspace tracking：The 13thEurope Signal Process Conference EUSIPCO'2005[C].EUSIPCO,2005.