钢管轻集料混凝土偏心受压构件承载力分析

(河海大学 土木与交通学院，江苏 南京，210098)

土木工程结构朝着高耸、大跨、重载的方向发展，恒载在结构的受力中占有较大比例。同时，高层建筑、大跨度桥梁、海洋工程等大型工程对材料性能的要求也越来越高。钢管混凝土中的核心混凝土可以延缓钢管的屈曲，而外包钢管使混凝土处于三向受压状态能增强其抗压性能，其组合力学性能超过了两者的叠加，充分利用了钢材的受拉和混凝土的受压特性。国内外学者对钢管混凝土构件的力学性能进行了大量的研究，已经形成了比较完善的理论体系[1−4]。轻集料混凝土密度较普通混凝土低20%～30%，故钢管轻集料混凝土密度要比钢管普通混凝土密度小，适应了现代材料轻质高强的发展需求。已有研究表明[5−9]：钢管轻集料混凝土同样具有优异的力学性能。尽管日本已有将钢管轻集料混凝土应用于“新干线”(高速铁路桥梁)的工程实例[10]，但对其性能的研究还未系统地开展。由于钢管混凝土本身的特性，通常用于受压构件。受材料的初始缺陷、材料不均匀性以及制造偏差等因素的影响，轴心受压状态很难实现。在外部横向力作用下，往往也使构件处于偏心受压状态[11]。本文作者在轴压和受弯研究的基础上，分析54根钢管轻集料混凝土偏压柱的试验结果，对偏心受压状态下钢管轻集料混凝土的承载力进行研究。

1 偏压试验

1.1 试验材料和装置

轻质混凝土骨料为页岩陶粒，其物理力学性能如下：堆积密度为814 kg/m3，筒压强度为8.5 MPa，1 h吸水率为 6%。水泥为普通硅酸盐水泥。混凝土的配合比和相应力学性能见表1。试验采用Q235直缝焊接钢管。试件的一端用10 mm厚的圆形钢板焊接封固。轻集料混凝土采用分层浇筑，最后用水泥浆抹平。试件养护10 d后将另一端也用10 mm厚的圆形钢板焊接封固，采取自然养护方式。

试验使用油压千斤顶加载，荷载由压力传感器测量，采用电阻应变计测量应变。在试件两端采用柱铰，在柱铰底部按偏心距分别设置 3个距中心为 10，20和35 mm的圆孔，孔径为20 mm，深为15 mm。试验时，用直径为20 mm、长25 mm的钢制榫头连接试件盖板和柱铰，保证当试件变形较大时试件与柱铰不发生脱离。试验装置见图1。

图1 试验装置及测点布置示意图Fig.1 Sketch map of loading and measurement system

试件采用分级加载的制度，当荷载达到最大值(极限值)时，压力传感器所示压力开始回落，仍继续向千斤顶油缸送油，直到试件挠曲非常明显为止。全过程采用数据自动采集系统进行连续数据采集。试验基本数据见表2。

1.2 试验结果分析

本次试验试件在偏心受压下的破坏形态可以分为以下2种情况：对于长径比较小(L/D=3，其中，L为试件长度，D为试件直径)的短柱偏压试件，试件破坏时发生侧向挠曲，中截面发生明显的局部屈曲(图2(a))，试件有较明显的强度破坏特征；对长径比较大的中长柱试件(L/D=7或14)，试件发生较大的侧向挠曲，钢管表面无明显屈曲，试件失稳破坏特征明显(图2(b))。根据中截面纵向应变分布，试件截面变形基本符合平截面假定[12]。

图 3所示为荷载−整体纵向应变曲线。在加载初期，荷载−纵向应变曲线基本上为直线，试件处于弹性阶段加载至比例极限后，曲线明显偏离其初始的直线，进入弹塑性工作阶段。当荷载接近极限荷载时，荷载的增长速度变慢，而纵向应变的增长速度加快。

表1 轻集料混凝土配合比和力学性能Table 1 Mixture ratio and mechanical properties of lightweight aggregate concrete

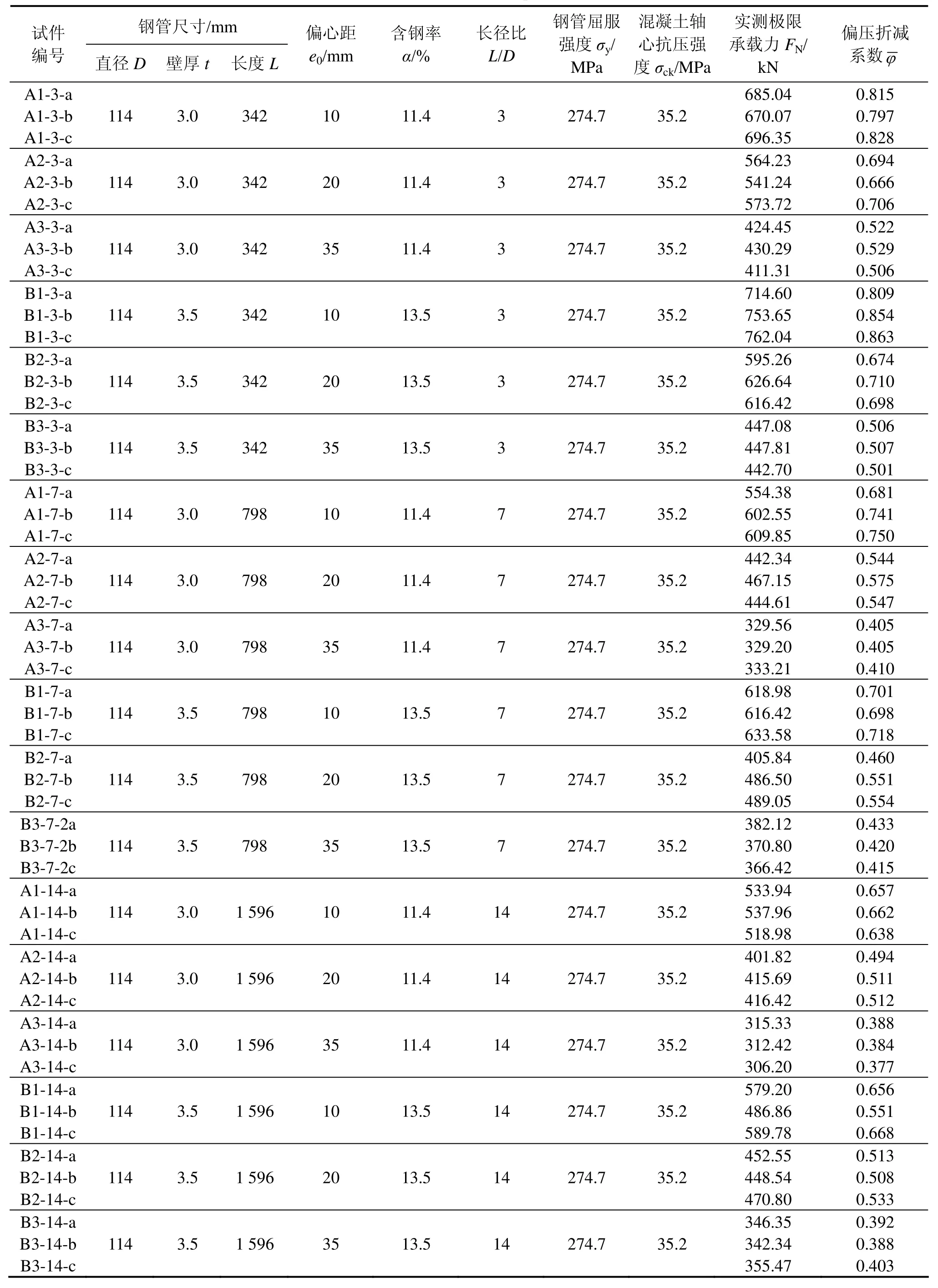
表2 试件基本数据及试验结果Table 2 Details of test specimens

图2 试件典型破坏形态Fig.2 Typical failure mode of specimen

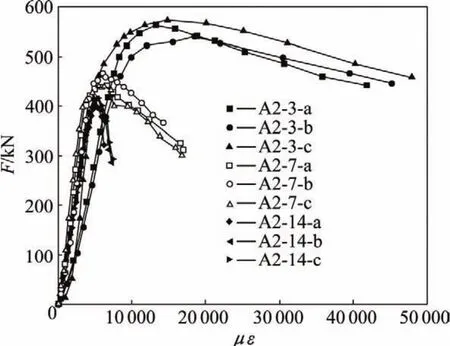
图3 荷载−整体纵向应变的关系Fig.3 Relationships of Load versus overall longitudinal strain

2 承载力影响因素

图4所示为各组试件在不同偏心率、不同长径比、不同含钢率下的荷载(F)−L/2处横向挠度(um)对比曲线。由图 4(a)可见：在同一组试件中，偏心率越小，则荷载−L/2处横向挠度曲线的初始斜率越大，极限承载力也越大；到达极限荷载后下降也越快。偏心率越大，构件所受到的弯矩越大，从而导致承载力降低。

图4(b)可见：试件的长径比越大，挠度增长越快，竖向力所产生的附加弯矩也越大。故长径比大的构件，曲线偏离初始直线越快，上升的斜率越小，其极限承载力也越低。

从图 4(c)可见：含钢率越高，曲线在弹塑性阶段的斜率也越大，试件的极限承载力也越高。因为钢材本身的受压性能高于混凝土的受压性能。同时，含钢率越大的试件，对核心轻集料混凝土紧箍力越大，对受压区轻集料混凝土强度提高越多。

图4 F-um曲线Fig.4 F-um curves

3 承载力规范计算比较

为了研究钢管轻集料混凝土构件偏心受压状态下的承载力计算方法，运用国内外多部针对钢管普通混凝土的规范[1−2]，包括 AISC—LRFD(1999)(美国钢结构协会提出的设计规程)、BS 5400(英国桥梁设计规程)、EC4(欧洲钢−混凝土组合结构设计规范)、DBJ 13—51—2003(福建省工程建设标准)、DL/T5058—1999(水工混凝土施工规范)、CECS 28：90(中国钢管砼结构设计与施工工程规范)，对本次试验的54根构件进行承载力计算，结果见表3。

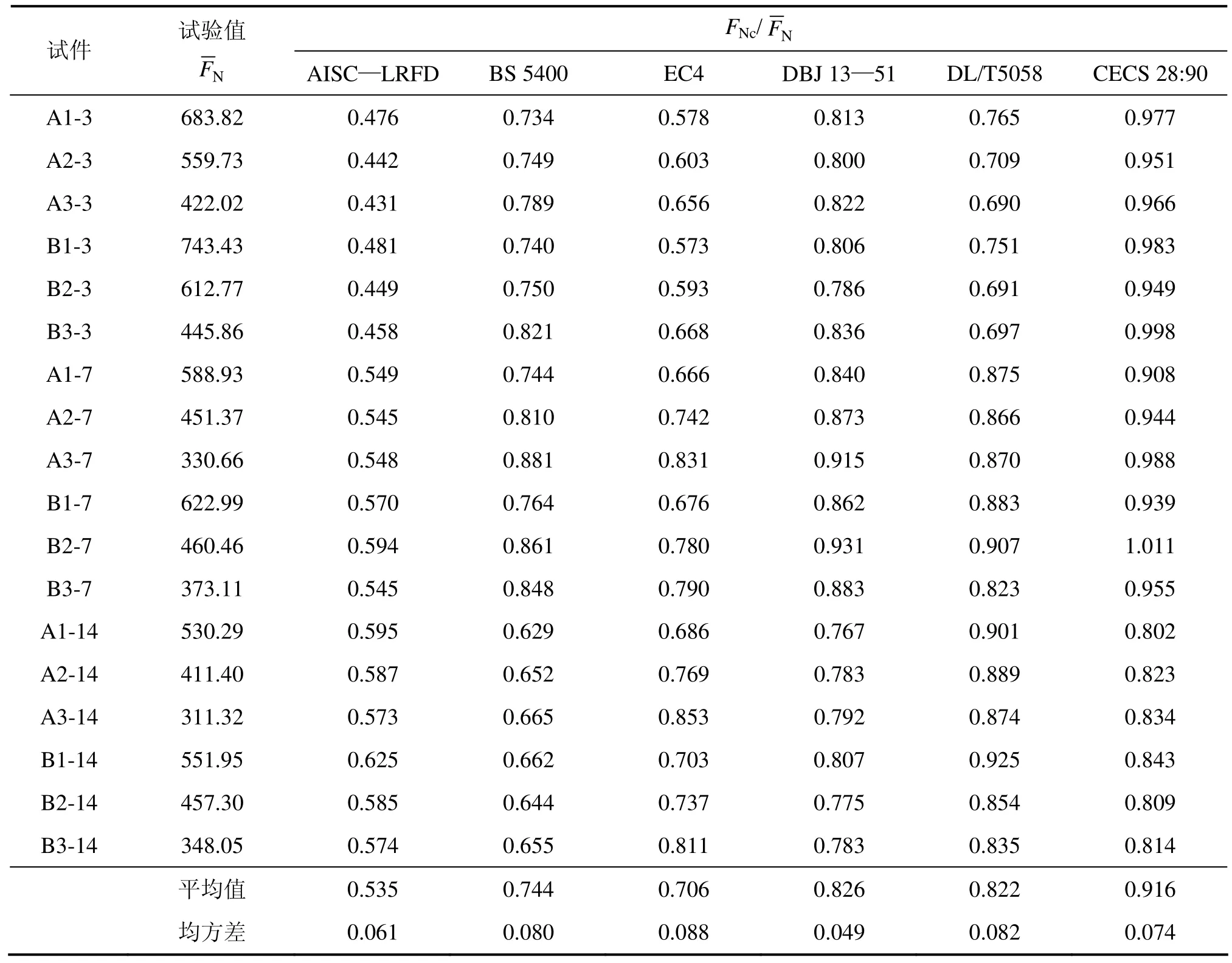
表3 偏压承载力规范计算Table 3 Bearing capacity calculation with different codes

由表3所示的对比结果可知：由规范所得计算结果均小于试验值，且由国外规范所得计算结果普遍较由国内规范所得计算结果小。除CECS 28：90以外，计算结果均相差较大。这可能是由于规范计算时要考虑一定的安全储备，并且钢管轻集料混凝土与钢管普通混凝土的力学性能存在差异。CECS 28：90的计算结果虽然与实测值比较接近，但应用其对钢管轻集料混凝土轴压短柱承载力计算结果偏高[5]。目前现有的计算方法对于钢管轻集料混凝土的适用性还有待进一步研究。

4 小偏心率FN/FNu-FM/FMu曲线

偏心受压加载相当于压弯构件的比例加载，可以采用构件FN/FNu-FM/FMu的及相关性曲线来考虑偏心受压构件的计算方法。在偏心率较小的情况下，FN/FNu-FM/FMu相关性曲线可以近似为 1条直线[1−2]。图5所示为FN/FNu-FM/FMu相关性曲线。由图5可知：对于偏心较小的情况，其曲线变化趋势可近似简化为线性关系。当FM/FMu=0时，FN/φFNu=1。故可用下式来计算小偏心率压弯构件承载力：

其中：FNu为短柱轴压极限承载力，取文献[8]中的实测值；FM和FMu分别为FN和FNu对应的偏心弯矩，FMu取文献[6]中壁厚2.5 mm和3.8 mm时最大弯矩的差值；φ为稳定系数，f为含钢率α和长径比λ等参数的函数。

对于A-3和B-3组短柱试件，φ=1。应用最小二乘法对试验实测值进行拟合。当α=11.4%时，f=0.446；当α=13.5%时，f=0.468。由于本次试验试样有限，各参数对斜率函数的影响以及大偏心率情况下承载力变化规律仍有待进一步研究。

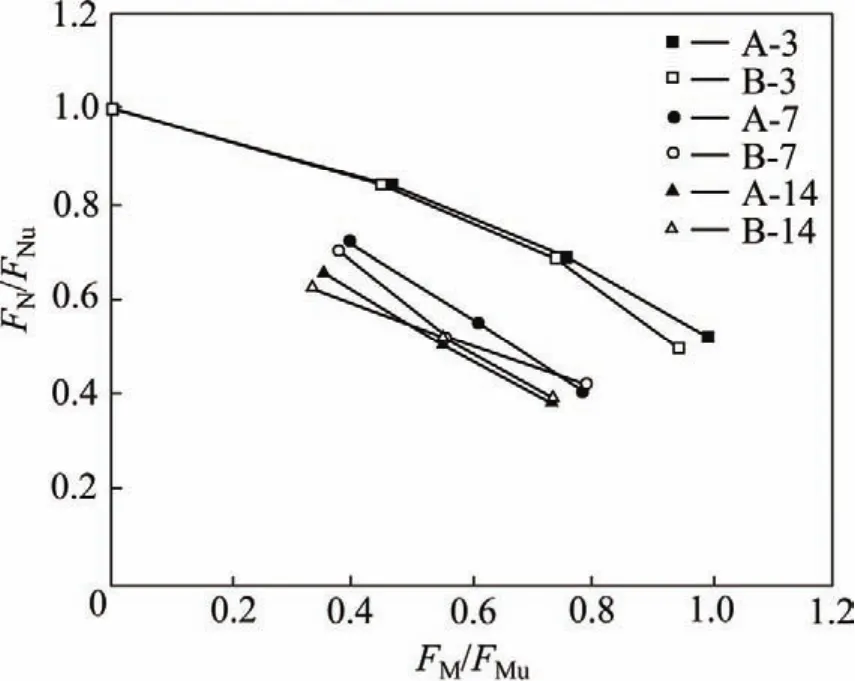
图5 FN/FNu-FM/FMu曲线Fig.5 FN/FNu-FM/FMu curves

5 结论

(1) 试件长径比影响构件破坏形态。试件长径比越小，越接近塑性破坏；长径比越大，越接近弹性破坏。

(2) 试件偏心率越大，长径比越大，含钢率越小，则钢管轻集料混凝土的极限承载力越低。

(3) 应用国内外规范所得计算结果比试验值小，现有规范对钢管轻集料混凝土的适用性还有待进一步研究。

[1] 蔡绍怀. 现代钢管混凝土结构[M]. 北京: 人民交通出版社,2003: 81−99.CAI Shao-huai. Modern concrete-filled steel tubular structures[M]. Beijing: China Communications Press, 2003:81−99.

[2] 韩林海, 杨有福. 现代钢管混凝土结构技术[M]. 北京: 中国建筑工业出版社, 2004: 93−357.HAN Lin-hai, YANG You-fu. Modern concrete-filled steel tubular structures technology[M]. Beijing: China Building Industry Press, 2004: 93−357.

[3] Kuranovas A, Goode D, Kvedaras A K, et al. Load-bearing capacity of concrete-filled steel columns[J]. Journal of Civil Engineering and Management, 2009, 15(1): 21−33.

[4] Zeghiche J, Chaoui K. An experimental behaviour of concrete-filled steel tubular columns[J]. Journal of Constructional Steel Research, 2005, 61(1): 53−66.

[5] 吉伯海, 王晓亮, 马敬海, 等. 钢管高强轻集料混凝土短柱轴压性能的试验研究[J]. 建筑结构学报, 2005, 26(5): 60−65.JI Bo-hai, WANG Xiao-liang, MA Jing-hai, et al. Experimental study on the behavior of high-strength lightweight aggregate concrete filled steel tube under axial compression[J]. Journal of Building Structures, 2005, 26(5): 60−65.

[6] 吉伯海, 胡正清, 陈甲树, 等. 圆钢管轻集料混凝土构件抗弯性能的试验研究[J]. 土木工程学报, 2007, 40(8): 36−42.JI Bo-hai, HU Zheng-qing, CHEN Jia-shu, et al. An experimental study on the behavior of lightweight aggregate concrete filled circular steel tubes under pure bending load[J].China Civil Engineering Journal, 2007, 40(8): 36−42.

[7] 吉伯海, 周文杰, 王晓亮. 钢管轻集料混凝土中长柱轴压性能的试验研究[J]. 建筑结构学报, 2007, 28(5): 118−123.JI Bo-hai, ZHOU Wen-jie, WANG Xiao-liang. Experimental study on the behavior of lightweight aggregate concrete filled steel tube middle long columns under axial compression[J].Journal of Building Structures, 2007, 28(5): 118−123.

[8] 傅中秋, 吉伯海, 胡正清, 等. 钢管轻集料混凝土长柱轴压性能试验研究[J]. 东南大学学报: 自然科学版, 2009, 39(3):546−551.FU Zhong-qiu, JI Bo-hai, HU Zheng-qing, et al. Experimental study on behavior of lightweight aggregate concrete-filled steel tube long columns under axial compression[J]. Journal of Southeast University: Natural Science Edition, 2009, 39(3):546−551.

[9] Moulia M, Khelafi H. Strength of short composite rectangular hollow section columns filled with lightweight aggregate concrete[J]. Engineering Structures, 2007, 29(8): 1791−1797.

[10] Shun-Ichi N, Yoshiyuki M, Tetsuya H, et al. New technologies of steel/concrete composite bridges[J]. Journal of Constructional Steel Research, 2002(58): 99−130.

[11] 张素梅, 郭兰慧, 王玉银, 等. 方钢管高强混凝土偏压构件的试验研究与理论分析[J]. 建筑结构学报, 2004, 25(1): 17−24.ZHANG Su-mei, GUO Lan-hui, WANG Yu-yin, et al.Experimental research and theoretical analysis of high strength concrete-filled square hollow section steel tubes subjected to eccentric loading[J]. Journal of Building Structures, 2004, 25(1):17−24.

[12] 陈宝春, 王来永, 欧智菁, 等. 钢管混凝土偏心受压应力−应变试验研究[J]. 工程力学, 2003, 20(6): 154−159.CHEN Bao-chun, WANG Lai-yong, OU Zhi-jing, et al.Experimental study of stress-stain relation of eccentricallyloaded concrete-filled steel tubular columns[J]. Engineering Mechanics, 2003, 20(6): 154−159.