自然气候环境的温度作用谱和混凝土内温度响应预计

(中国矿业大学 力学与建筑工程学院，江苏 徐州，221008)

温度是钢筋混凝土结构耐久性问题的重要影响因素之一，针对自然环境下混凝土的碳化、氯盐侵蚀和钢筋锈蚀等问题，研究者们开展了大量关于温度影响的研究[1−12]。人工气候环境下混凝土内温度响应的研究成果表明：在恒定温度环境下，混凝土内温度需要一段时间才能达到与环境温度一致[13]。而实际的钢筋混凝土结构处于自然环境作用下，自然环境与人工气候环境相比，其温度随时间发生波动，从而影响自然环境下混凝土内温度的响应规律。同时，对于混凝土结构耐久性问题，其直接的影响因素是混凝土内温度，而并非自然环境温度，但在目前的很多研究中，将影响温度视为环境温度，因此，为了进行自然环境下钢筋混凝土结构的耐久性使用寿命预计，研究自然气候环境下混凝土内温度响应规律是必要的。本文作者通过人工气候与自然气候条件下混凝土内外温度的监测，分析混凝土内部微环境温度对自然环境温度的滞后响应规律，提出自然环境温度的处理方法，构筑成自然气候环境温度作用谱；基于混凝土内温度响应预计模型，得到混凝土内温度响应规律，从而为混凝土碳化、氯盐侵蚀和钢筋锈蚀速率的预计提供直接依据。

1 气候环境下混凝土内温度响应试验

1.1 试验方案

1.1.1 试验目的

通过对混凝土试件内外温度的监测，研究人工气候环境与自然气候环境下混凝土内温度与外部环境温度的响应规律，为最终建立混凝土内温度响应预计模型以及构筑自然环境的温度作用谱和混凝土温度响应谱奠定基础。

1.1.2 试件设计

试件采用C25混凝土，水泥、砂子、石子和水的质量比为mC:mS:mG:mW=1.00:1.75:2.98:0.55。水泥采用徐州淮海水泥厂生产的巨龙牌P.O32.5普通硅酸盐水泥，砂子采用本地产河砂(中砂)；石子采用本地产碎石，其主要成分为石灰岩和粗面岩，粒径为5～15 mm，级配良好；水采用普通自来水。

试件尺寸(长×宽×高)为150 mm×150 mm×100 mm，在混凝土试块内埋置温度探头，探头距混凝土表面的距离为25 mm，试件制作示意图如图1所示。本试验共制作试件3块，分别为RT-1，ZY-1和ZY-2。

1.1.3 试验过程与方法

同时开展人工气候条件与自然环境下有遮蔽条件的混凝土温度响应试验，试验条件如表1所示。

(1) 人工气候环境下混凝土内温度响应试验。温度响应试验在人工气候环境室内进行，该人工气候室能根据试验要求，保持恒温恒湿的环境条件。首先，试件脱模后放入标准养护室内养护28 d；取出后放置在室内自然环境7 d；试验时，测定试件的初始温度t0，并控制混凝土的含水率；然后，设定人工气候室内的环境温度t∞，待气候室内温度达到恒定后，将温度响应试件放入；每隔一定时间，根据试件内埋设的温度探头记录试件混凝土内部25 mm深度位置的温度t。试验进行至混凝土内温度与环境温度一致为止。

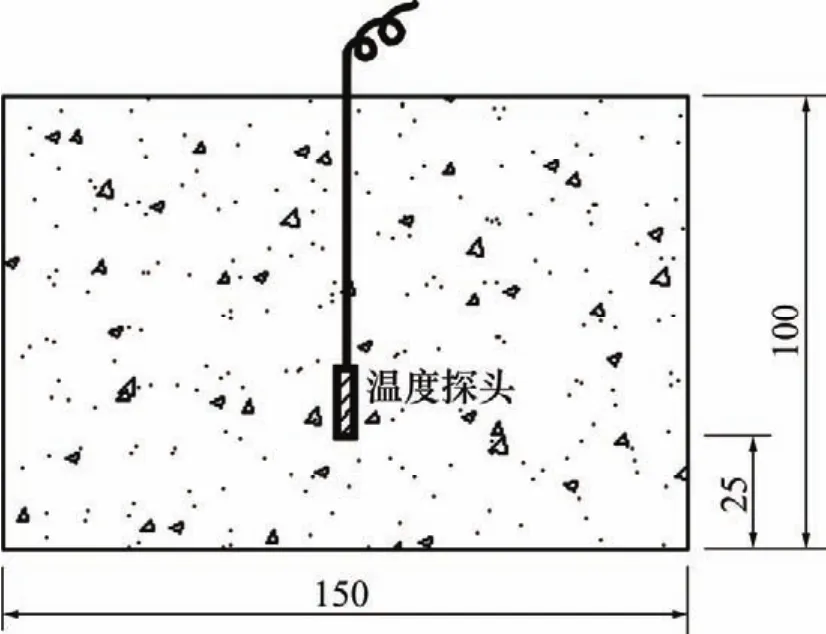
图1 试件制作示意图Fig.1 Sketch of concrete specimen

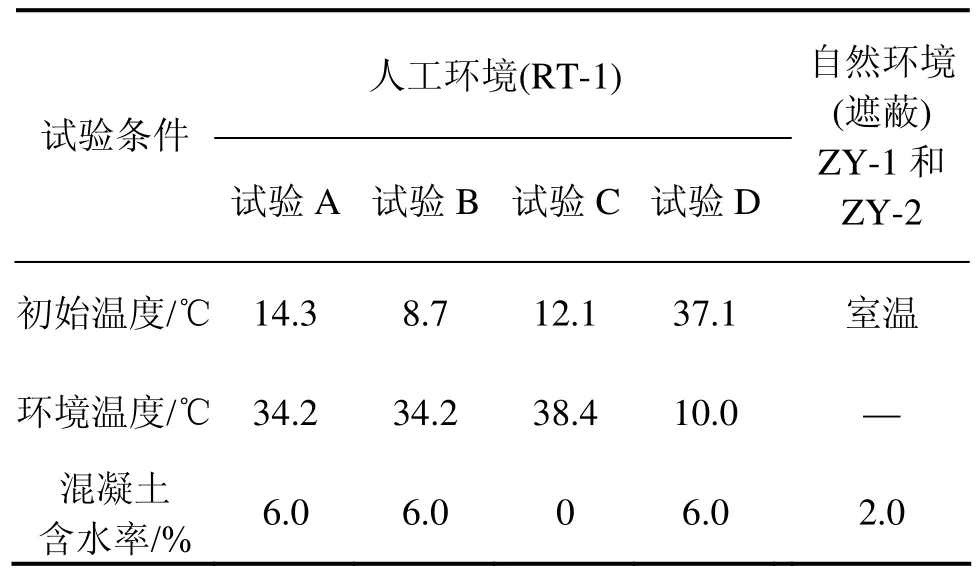
表1 温度响应试验条件Table 1 Test condition for temperature response

(2) 自然气候环境下混凝土内温度响应试验。试件制作完成并养护28 d后，由于此时混凝土的含水率较大，因此，在开始自然环境下的试验之前，先将试件进行适当烘干，使混凝土含水率控制在 2%左右。试验暴露地点为中国矿业大学结构实验室(江苏徐州)室外自然气候环境中，试件处于有遮蔽条件，即试件不直接受到雨淋和太阳光照，试件放置的平面距离地面约0.5 m。

1.2 人工气候环境下混凝土内温度响应规律

根据实测数据绘制出不同温湿度组合条件下，混凝土内部(25mm)温度随时间的演变曲线，部分结果如图2和图3所示。

根据上述试验结果，在人工气候环境下，混凝土内温度与环境温度间的响应具有以下规律：

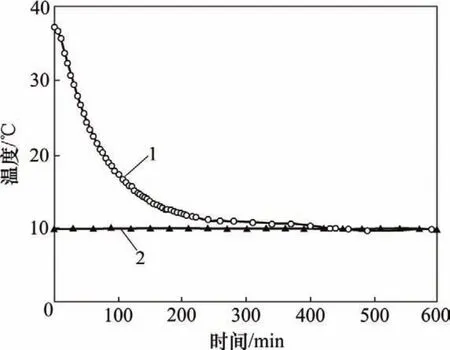
图3 试验D混凝土内温度响应曲线(降温)Fig.3 Temperature response curve of concrete in test D(Cooling)

(1) 不同环境组合条件下，混凝土内部温度随时间的变化规律非常相似，混凝土内部温度均滞后于环境温度，内部温度需要一段时间以后才能达到与环境温度相一致。

(2) 混凝土内部温度在初始时期均变化(上升或下降)较快；随着时间的推移，混凝土内部温度变化速率逐步减慢；最后，混凝土内部(25 mm)温度趋于与环境温度一致。

(3) 混凝土内外初始温差对混凝土内温度的初始变化速率影响明显。混凝土内外初始温差越大，则混凝土内温度的初始变化速率越快；经过一段时间之后，随着内外温差的减小，温度的变化速率逐步趋于平缓。

1.3 自然气候环境下混凝土内温度响应规律

在自然环境下的混凝土温度响应试验过程中，利用温度探头同时监测混凝土内(25mm处)、外温度的演变情况，并利用记录器定时记录温度，部分结果如图4和图5所示。

图4 试件ZY-1混凝土内外温度演变规律的比较Fig.4 Comparison of temperature evolution rules between inside and outside concretes for specimen ZY-1

图5 试件ZY-2混凝土内外温度演变规律的比较Fig.5 Comparison of temperature evolution rules between inside and outside concretes for specimen ZY-2

从图4和图5可以看出在自然环境下，环境温度的变化与混凝土内温度的响应具有如下规律：

(1) 自然环境中的温度随时间而波动，并具有简单的昼夜周期性；同时，混凝土内的微环境受到自然环境的影响，混凝土内温度也随时间而波动。

(2) 混凝土经历了升温与降温的循环过程，混凝土内、外温度的变化趋势基本一致，但混凝土内温度的波动曲线相对光滑。

(3) 混凝土内温度与外部环境温度间存在一定滞后性：当处于升温段时，混凝土内温度低于外部环境温度；当处于降温段时，则混凝土内温度高于外部环境温度。

2 气候环境下混凝土内温度响应的滞后效应分析

2.1 人工气候下混凝土内温度响应预计模型

理论分析和试验研究结果表明：环境温度对混凝土内部的影响过程其实是一个传热的过程。处于一定环境气候条件下的混凝土的传热，其实质为传热学上换热边界条件下的非周期性非稳态导热问题[14]。已知混凝土试块的三轴尺寸分别为 2δx，2δy和 2δz，混凝土内部初始温度(均匀一致)为t0，环境温度(瞬间恒定不变)为∞t，气候环境与混凝土间的表面传热系数h为常数，混凝土的导热系数为λ，导温系数为a。基于傅里叶导热基本定律和能量守恒原理，可以建立恒定人工气候下混凝土内温度响应的预计模型：

其中，∞-=tt00θt(x,y, z,τ)为混凝土内任意位置(x,y,z)在任意时刻(τ)的温度；),(τθi为任意位置任意时刻的过余温度，i=x,y,z；0θ为初始时刻过余温度；inβ为超越方程的根；Bi为毕渥数，

关于人工气候环境下混凝土内温度响应预计模型的研究内容，将在另外的文献中做具体阐述，因此，本文只做简单介绍。

2.2 恒定气候温度环境下混凝土内温度响应的滞后效应分析

温度响应“滞后时间”是混凝土内温度与环境温度响应过程的一个重要指标，它定量地反映了混凝土内温度响应的速度。下面具体分析混凝土温度响应滞后时间的相关规律。

2.2.1 初始温差变化对“滞后时间”的影响

图6所示为混凝土温度响应滞后时间随混凝土内外初始温差(0ttt-=Δ∞)的变化规律，取混凝土导热系数λ=1.2 W/(m·K)和表面传热系数h=25 W/(m2·K)。从图6可以看出：当初始温差从5 ℃变化到45 ℃时，相应的温度响应滞后时间增长幅度仅为 31.9%。而且随着初始温差的增大，温差变化对响应滞后时间的影响越来越小。

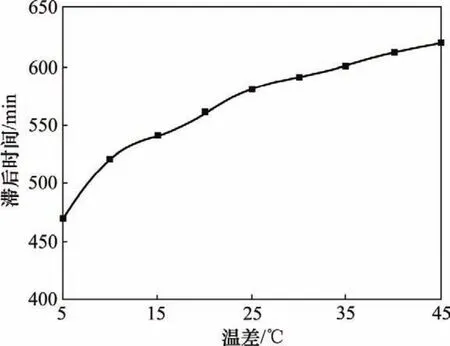
图6 混凝土温度响应滞后时间随初始温差的演变曲线Fig.6 Evolution curve of concrete temperature response hysteretic time with initial temperature difference

2.2.2 混凝土导热系数λ及表面传热系数h对“滞后时间”的影响

前面对混凝土温度响应滞后时间的分析是基于λ和h为定值的前提。而在实际环境中，随着环境条件的变化，λ和h可能会发生改变。

经试验测定，普通混凝土常温下的导热系数为1.0～2.0 W/(m·K)。因此，在其他参数一定的前提下，利用混凝土温度响应模型讨论滞后时间随导热系数的变化规律，结果如图7所示。

从图7可以看出：温度响应滞后时间随混凝土导热系数的增大而减小。这主要是因为导热系数越大，混凝土内的温度响应越快，故响应的滞后时间越短；而且，混凝土温度响应滞后时间随导热系数的演变服从指数函数的规律。

同理，可以利用温度响应模型来分析混凝土表面传热系数h对混凝土内温度响应滞后时间的影响，结果如图8所示。

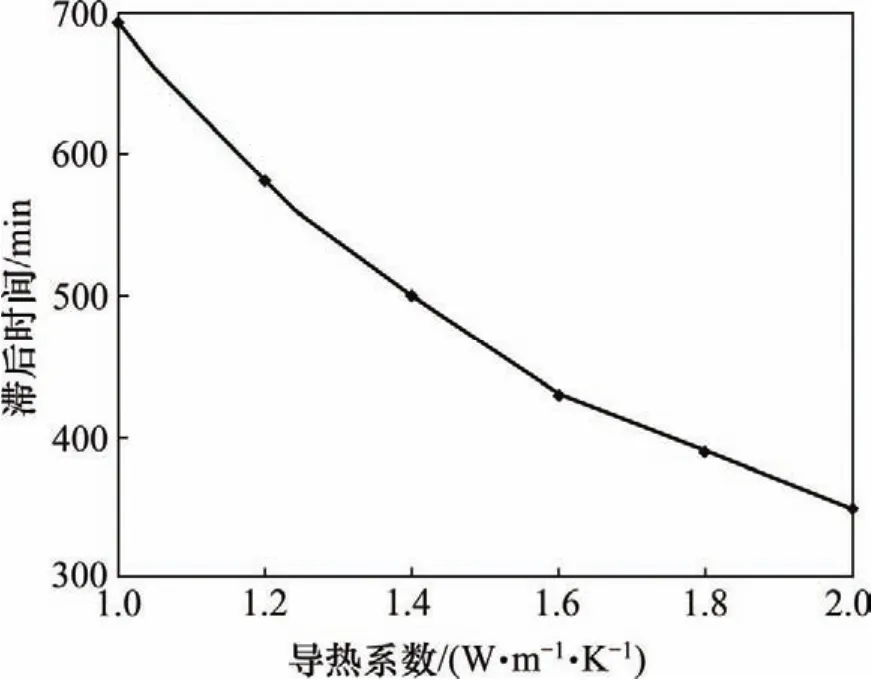
图7 温度响应滞后时间随导热系数的演变曲线(h=25)Fig.7 Evolution curve of temperature response hysteretic time with thermal conductivity (h=25)

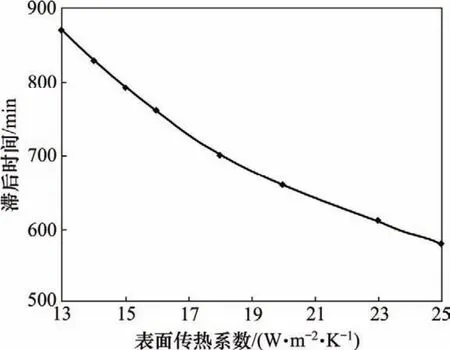
图8 温度响应滞后时间随表面传热系数的演变曲线(λ=1.2)Fig.8 Evolution curve of temperature response hysteretic time with surface heat-transfer coefficient (λ=1.2)

从图8可以看出：在其他条件一定时，温度响应滞后时间随表面传热系数的增大而减小。这是因为混凝土与环境的温度响应过程包括2个阶段，即环境与混凝土表面的传热(换热)阶段(Ⅰ)和混凝土导热阶段(Ⅱ)，而混凝土表面传热系数h决定了第Ⅰ阶段的快慢。

2.3 自然气候环境下混凝土内温度响应的滞后效应

自然环境下混凝土内温度的日变化如图9所示。可见：混凝土内温度响应与环境温度的变化在时间上和数值上均存在滞后性。

从图9可以看出：混凝土内温度与环境温度的谷值点和峰值点出现的时间存在滞后，与环境温度相比，混凝土内温度出现峰值的时间滞后 1～3 h，出现谷值点的滞后时间一般为1 h左右。此外，从温度来看，当混凝土与环境同时处于降温过程时，混凝土内温度高于环境温度，而升温时，环境温度要高于混凝土温度；只有在混凝土内温度的谷值点和峰值点时，混凝土内温度与环境温度一致。因此，如果忽略混凝土内温度的谷值点和峰值点，那么自然环境下混凝土内温度响应与人工气候环境下的响应规律相比，最显著的区别就是混凝土内温度与环境温度无法达到一致。

图9 自然环境下混凝土内温度响应滞后性示意图Fig.9 Schematic diagram of concrete temperature response hysteretic natures under natural environment

3 基于自然气候环境温度变化的温度作用谱

由于自然环境温度随时间而发生周期性和非周期性波动，这为研究自然环境下混凝土内温度的响应增加了难度。因此，为了便于混凝土微环境温度响应的预计，必须对实际的自然环境温度进行一定简化处理。本文将处理后得到的温度演变曲线称为自然环境“温度作用谱”。

3.1 温度作用谱构筑原则及理论分析

构筑环境温度作用谱的总体原则是：实现对自然气候环境温度资料的简化处理，构筑的温度作用谱要能较好地反映实际环境温度的作用规律；同时，在温度作用谱下得到的混凝土微环境温度响应要能代表自然环境下混凝土内温度的真实响应。

为了探讨自然环境温度资料的简化处理方法，引入“极差分割法”[15]。“分割法”是聚类分析中的一个方法，它所处理的是一类与顺序有关的分类问题，即将一长串资料分割成几段。在统计学上，描述一组数据内部不整齐的程度可以用这组数据的方差或标准差，但计算这2个量比较繁琐，通常用极差来代替。数据x1，…，xn的极差为

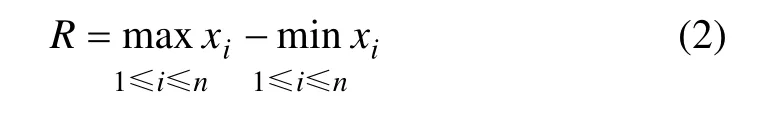
显然，极差很容易计算，而且能反映一组数据内部不整齐的程度。

为了便于讨论，提出“k分割”的概念，即把n个有顺序的数据x1，…，xn分割成k段。

“极差分割法”的总体原则是：对一组数据分段后，每一段内部数据之间的差异越小越好。其具体方法为：对于n个有顺序的数据x1，…，xn，考虑其所有可能的k分割，每一个k分割都把这n个数据分成k段，分别计算这k段的极差，用R1,R2, …,Rk表示；R1,R2, …,Rk越小越好。也就是说，找到使maxRi达到最小值时的k分割，就可以求出最优的k分割。

对于1月内的温度数据，讨论气温的日变化情况。1 d中气温的最高值和最低值之差，称为“气温日较差”，即温度极差R，反映了气温日变化的程度。因此，对于24 h的自然气温数据，可以采用“极差分割法”对其进行分段。

3.2 温度作用谱构筑方法

混凝土内温度响应滞后效应的分析结果表明，混凝土的导热系数、初始温度差及表面传热系数对响应滞后时间存在影响，同时，对于自然环境下的混凝土内温度响应，还存在混凝土内温度基本无法达到与环境温度一致的数值滞后性。如果在一定条件下能将自然环境转化为相似的人工环境，取自然环境下混凝土导热系数λ=1.32 W/(m·K)，混凝土表面传热系数h=12.8 W/(m2·K)(考虑风速v=0.1 m/s)，而自然环境下混凝土内外温差一般为1～7 ℃，基于人工气候环境下的混凝土内温度滞后时间分析结果，此时，混凝土内温度响应的滞后时间为9～12 h。

基于上述理论分析和总体原则，并结合“极差分割法”的相关原则，采取“三分割”形式，即将24 h的自然环境温度资料划分为3段。于是，自然环境温度作用谱的构筑方法可表述如下。

第1步：将自然环境下每天24 h的温度采用“极差分割法”划分为3段。

第2步：在分割后的每一段内，用平均温度代替原始温度。

图10所示为对某天的温度进行“三分割”简化处理的结果。从图10可以看出，采用“三分割”处理方式，不仅满足每段的时间跨度不超过9～12 h，而且基本满足了各段温度波动最小的要求。

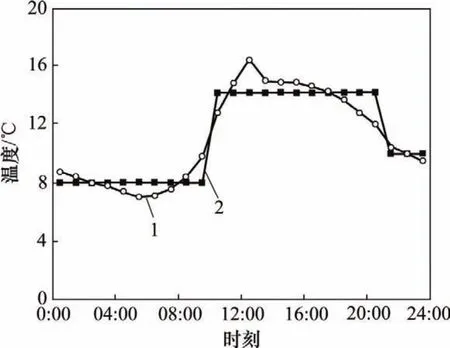
图10 自然环境下日温度处理结果Fig.10 Treatment results of daily temperatures in natural environment

4 基于温度作用谱的混凝土微环境温度响应预计

4.1 预计方法

在建立了自然环境的温度作用谱基础上，利用人工气候条件下混凝土温度响应的研究成果来预计混凝土内的温度，并将预计的混凝土内温度演变规律称为混凝土微环境的“温度响应谱”。

根据自然环境温度作用谱的建立方法，按照极差最小的原则，将环境温度分割为3段，在每一段内将温度视为恒定；因此，在划分的每一段内，可将自然环境下的混凝土温度响应看作恒定温度人工气候下的混凝土温度响应过程，于是，可以利用人工气候环境下的混凝土内温度响应预计模型来计算混凝土内温度瞬时值。具体方法如下。

第1步：将首日0:00～9:00的平均温度作为混凝土的初始温度t0。根据试验结果，在这一时间段内，混凝土内温度与环境温度比较接近。

第2步：将10:00～20:00的平均温度视为∞t，于是，混凝土内的温度响应过程可视为初始温度为t0，环境温度恒定为∞t的人工气候响应过程，利用温度响应模型公式(1)预计混凝土内温度。

第3步：在21:00～23:00，将时间点20:00的混凝土内温度预计值作为新的混凝土初始温度t0，以这一时间段的平均环境温度作为∞t，利用式(1)预计混凝土内温度。

第4步：将首日23:00时刻的混凝土内预计温度作为次日混凝土的新初始温度t0，在次日 0:00～9:00时间段内，按照步骤2来预计混凝土内的温度。

最后，重复第2～4步，便可求得在自然环境温度作用谱下混凝土内的温度响应值。

4.2 混凝土内温度响应计算曲线和实测曲线比较分析

在获得自然环境下混凝土内外温度的长期监测资料基础上，首先，构筑自然环境的温度作用谱(如图11所示)；然后，基于自然环境的温度作用谱，按照上述混凝土内温度响应预计方法，得到混凝土内温度的响应谱，并与自然环境下实测的混凝土内温度进行比较(如图12所示)。比较结果表明，自然环境温度“作用谱”及混凝土内温度“响应谱”均与实测结果吻合较好。

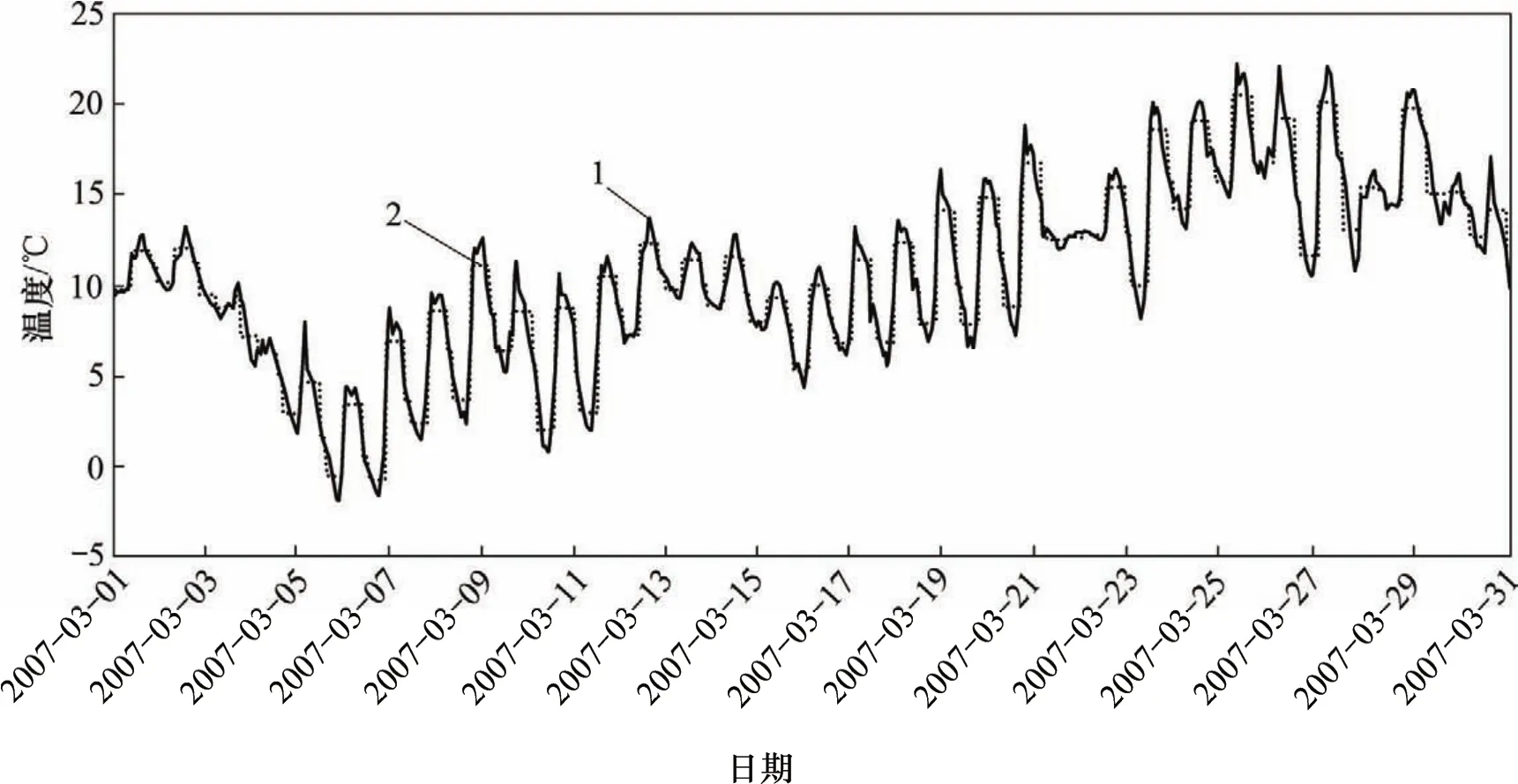
图11 自然环境温度作用谱与实测值的比较Fig.11 Comparison between natural environment temperature action spectrum and actual temperature

图12 混凝土温度响应谱与实测值的比较Fig.12 Comparison between temperature response spectrum and actual temperature of concrete

5 结论

(1) 人工气候环境下，混凝土内部微环境温度与外界环境温度之间的响应存在一定滞后性，即混凝土内部温度要达到与环境温度相一致，存在一个滞后时间。

(2) 在自然环境下，混凝土内、外温度的变化趋势基本一致，并具有简单的昼夜周期性；但混凝土内温度与环境温度之间的响应也存在一定滞后性。

(3) 自然环境下，混凝土内外温度间的滞后性体现在2个方面：一是时间滞后，即两者在峰值和谷值出现的时间上存在滞后；二是数值滞后，混凝土内外温度基本上无法达到一致。

(4) 基于混凝土内温度响应的滞后规律，并采用“极差分割”的数学方法，提出了对波动变化的自然环境温度资料的处理方法，进而构筑成自然环境的温度作用谱；并利用人工气候下的混凝土温度响应预计模型，实现了对自然环境下混凝土内温度响应的预计，建立了自然环境下混凝土内温度响应谱。

[1] Liu T, Weyers R W. Modeling the dynamic corrosion process in chloride contaminated concrete structures[J]. Cement and Concrete Research, 1998, 28(3): 365−379.

[2] Nguyen T S, Lorente S, Carcasses M. Effect of the environment temperature on the chloride diffusion through CEM-I and CEM-V mortars: An experimental study[J]. Construction and Building Materials, 2009, 23(2):795−803.

[3] Saetta A V, Schrefler B A, Vitaliani R V. The carbonation of concrete and the mechanism of moisture, heat and carbon dioxide flow through porous materials[J]. Cement and Concrete Research, 1993, 23(4): 761−772.

[4] Pour-Ghaz M, Isgor O B, Ghods P. The effect of temperature on the corrosion of steel in concrete. Part 1: Simulated polarization resistance tests and model development[J]. Corrosion Science,2009, 51(2): 415−425.

[5] Sabine C. Effect of temperature on porosity and on chloride diffusion in cement pastes[J]. Construction and Building Materials, 2008, 22(7): 1560−1573.

[6] 张海燕, 把多铎, 王正中. 混凝土碳化深度的预测模型[J]. 武汉大学学报: 工学版, 2006, 39(5): 42−45.ZHANG Hai-yan, BA Duo-duo, WANG Zheng-zhong. A model for forecasting carbonization depth of concrete[J]. Engineering Journal of Wuhan University, 2006, 39(5): 42−45.

[7] 余红发, 孙伟, 麻海燕, 等. 混凝土在多重因素作用下的氯离子扩散方程[J]. 建筑材料学报, 2002, 5(3): 240−247.YU Hong-fa, SUN Wei, MA Hai-yan, et al. Diffusion equations of chloride ion in concrete under the combined action of durability factors[J]. Journal of Building Materials, 2002, 5(3):240−247.

[8] Zivica V, Krajci L, Bagel L, et al. Significance of the ambient temperature and the steel material in the process of concrete reinforcement corrosion[J]. Construction and Building Materials,1997, 11(2): 99−103.

[9] Nassar M M. The Effect of environmental temperature on the corrosion of reinforced concrete[J]. Corrosion Prevention and Control, 1997, 44(6): 167−172.

[10] 耿欧, 袁迎曙. 混凝土氧气扩散系数试验研究[J]. 东南大学学报: 自然科学版, 2006(S2): 191−194.GENG Ou, YUAN Ying-shu. Experimental study on diffusion coefficient of oxygen in concrete[J]. Journal of Southeast University: Natural Science Edition, 2006(S2): 191−194.

[11] Samson E, Marchand J. Modeling the effect of temperature on ionic transport in cementitious materials[J]. Cement and Concrete Research, 2007, 37(3): 455−468.

[12] Vodak F, Trtik K, Kapickova O, et al. The effect of temperature on strength – porosity relationship for concrete[J]. Construction and Building Materials, 2004, 18(7): 529−534.

[13] 马文彬. 气候环境变化与混凝土内微环境的响应规律研究[D].徐州: 中国矿业大学建筑工程学院, 2007: 29−38.MA Wen-bin. Response regularity of microenvironment in concrete under climate variations[D]. Xuzhou: China University of Mining and Technology. School of Architecture and Civil Engineering, 2007: 29−38.

[14] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社, 2006:63−85.YANG Shi-ming, TAO Wen-quan. Heat transfer[M]. Beijing:Higher Education Press, 2006: 63−85.

[15] 张尧庭, 赵溱, 陈应强. 气象资料的统计分析方法[M]. 北京:农业出版社, 1979: 68−78.ZHANG Yao-ting, ZHAO Zhen, CHEN Ying-qiang. Statistical analysis methods for meteorological data[M]. Beijing:Agricultural Press, 1979: 68−78.