冲击损伤对PDC侧压强度的影响

陈枫，徐根，徐国平，马春德

(1. 中南大学 现代分析测试中心，湖南 长沙，410083；2. 中南大学 资源与安全工程学院，湖南 长沙，410083；3. 金瑞新材料科技股份有限公司，湖南 长沙，410012)

聚晶金刚石复合片(Polycrystalline diamond compacts，简称 PDC)是由聚晶金刚石层(PCD)与WC-Co硬质合金基体烧结而成，已经广泛应用于钻探及机械加工领域[1−3]。PDC钻头在正常使用情况下，其使用寿命取决于金刚石层(PCD)的耐久性，PCD层的严重磨损会大大降低钻头的钻进效率[4−6]。若能将局部磨损的PDC进行有效的二次利用，则可以降低钻头的钻进成本。国外很早就有将磨损的PDC进行二次利用的例子[7]，目前国内尚无此做法。其主要原因在于：在局部磨损的PDC内不可避免地存在损伤、裂纹等不确定因素，无法判断使用性能的稳定性，若二次使用会有很大的风险，而对于这方面的研究也未见报道。因此，研究损伤对PDC使用性能的影响，对于PDC的二次利用从而有效降低钻探成本意义重大。为了保证PDC钻头的钻进效率，充分利用PCD材料高硬度、高耐磨性的特点，在其工作时必需始终保持PCD层刃缘与岩石相接触。因此，PDC钻头在钻探时其工作面与岩石切削面之间具有特定的角度，在钻探过程中钻头所受荷载与用落锤等方法测试 PDC抗冲击强度时所受的荷载有所不同，该荷载与钻头钻压、转速、地形等因素相关[8]。本文定义在特定的工作角度下PCD层刃缘的抗压强度为PDC的侧压强度。

本文作者利用 Instron1342型材料试验机及霍布金逊压杆(SHPB)装置[9]，进行了同种PDC试样在不同加载速率下的侧压实验和不同 PCD层厚度试样的冲击破坏实验，并模拟磨损PDC二次利用时的受载荷方式(即认为第1次破坏时，已对PDC造成内在损伤)，采用沿直径对边第2次破坏性加载，测量PDC试样损伤前后的侧压强度，并对各加载方式下PDC的破坏模式进行研究。

1 实验方法与步骤

1.1 实验方法

本次实验试样直径×长度为19 mm×13 mm、复合片PCD层中含94%(体积分数)的金刚石，含6%(体积分数)的钴(D6Co)，基体则采用高钴含量的 WC-Co硬质合金YG15。金刚石平均粒度为28 μm，金刚石层表面经过研磨处理，试样形貌如图1所示，PDC各合成材料参数见表1。

为了模拟磨损PDC二次利用时的受载荷方式，研究PDC试样损伤前后侧压强度的变化，采用沿直径对边加载的方式，即每个PDC试样沿同一直径两端进行2次破坏性加载，加载装置见图2。为更好地模拟PDC钻具在实际工作时的受载条件，加载角α与 PDC钻探时工作面与岩石之间夹角相同，取 20º。另外，由于PCD层硬度极大，为了保护加载装置及减少加载装置变形对测试结果的影响，使结果更具有可比性，PCD层与加载装置之间放置了 PDC衬垫，即形成PCD-PCD的接触方式。加载装置示意图如图2所示。

图1 PDC试样示意图Fig.1 Sketch map of PDC Specimen

表1 20 ℃时PDC材料参数Table 1 Material properties of PDC at 20 ℃

图2 加载装置示意图Fig.2 Schematic diagram of loading device

1.2 PDC侧压强度的准动态实验研究

利用 Instron1342型材料试验机，对同品种与规格、同PCD层厚度的试样进行不同加载速率下的侧压实验，得到每种加载速率下 PDC损伤前后的侧压强度。实验所使用PDC试样，其PCD层厚度均为1.5 mm，其余尺寸见图1。其中，Instron试验机采用位移控制方式加载，并采用5个不同等级的加载速率。采用低周疲劳的加载方式，即选用大幅值(超过试件强度)、小周期数(1个周期)来实现对PDC的准动态加载，并采用正弦波加载[10]，采样频率为5 kHz。图3所示为试样的载荷−位移曲线(不考虑由加载装置变形引起的误差，这里只给出静态2次加载的载荷−位移曲线)，通过该曲线计算得到试样的侧压强度(用侧压能表示)以及单位时间内试样吸收的侧压能。

PDC侧压能及单位时间内吸收的侧压能与 PCD层厚度的关系如图4所示。由图4可知：PDC试样损伤后侧压强度与加载速率的变化规律与损伤前相同，即：加载速率越大，PDC损伤前后抗侧压强度也越大，加载速率与侧压强度之间呈非线性关系。应变率数量级 10−6，10−5和 10−4均属于静态加载范围，前后 2次侧压能均比较接近，进入准动态加载范围后，PDC侧压能开始迅速增长，当应变率达到10−2量级时，PDC侧压强度为静态(应变率10−6量级)的7.29倍。从前、后2次加载的侧压差异来看，其变化规律也有相同的趋势：静态加载范围相差较小，而在准动态加载下，前、后2次加载PDC侧压强度有较大差异。PDC受载荷后内部出现的损伤以及由此引起的应力重分布是前、后2次加载侧压强度出现差异的主要原因。图4说明：PDC内部的损伤随着加载速率的提高而增大。

图3 应变率为1.667×10−6时PDC试样损伤前后载荷−位移曲线Fig.3 Variation curves of load with displacement while strain rate is 1.667×10−6

图4 试样侧压能与加载速率的关系Fig.4 Relationship between edgewise compressive energy and loading speed

图5所示为静态(应变率10−6量级)和准动态(应变率10−2量级)加载条件下前、后2次加载得到的试样破坏形貌。结合图4(b)和图5可以发现：在静态条件下前、后2次加载，试样单位时间内吸收侧压能极少，且前、后2次变载变化亦不大，因而PCD层破坏范围均较小，且均未达到界面以下，即破坏仅发生在PCD层。这说明：在静态加载条件下，PDC试样内部的损伤仅发生在加载点附近的一个较小范围内。相对于静态加载，在准动态加载条件下，试样单位时间内吸收的侧压能大4个量级，且前、后2次加载侧压能下降了21.2%，说明第1次侧压加载在试样内部引起的损伤较为严重，试样PCD层出现了一定范围的崩裂，但尚未引起脱层(见图5(b))。显然，加载速率越大，PDC试样单位时间内吸收的侧压能越多，试样破坏越严重。

加载速率与损伤面积之间的关系曲线如图 6所示。从图6可见：随着加载速率的增大，试样2次加载分别引起的损伤面积 均随之增大，且第2次加载引起的损伤面积均比第1次的要大，前、后两次加载引起损伤面积之间的差值亦随着加载速率的增大而增大。结果表明：PDC内部损伤不但与加载速率相关，而且损伤存在累积效应，即第2次冲击损伤是2次侧压所引起的损伤共同作用的效果。因而，经历第1次损伤后的PDC若再次利用，其抗侧压强度会下降，且加载速率越大，强度下降越明显。

图5 Instron 2次加载试样的断口形貌Fig.5 Failure models of PDC tested by Instron 1342 testing machine

图6 加载速率与损伤面积的关系Fig.6 Relationship between damaged area and loading speed

1.3 PDC侧压强度的冲击实验研究

本实验利用SHPB冲击加载装置，对同规格、不同PCD层厚度的试样进行侧压加载实验。PCD层厚度h分别为0.5，1.0，1.5和2.0 mm。其中：SHPB装置所采用弹性杆直径为50 mm，长度为2 m，材料为40Cr合金钢；采样频率为5 kHz，气压为0.8 MPa，无预压应力。应变片型号为B×120−2AA型，测试系统为CS−1D型超动态应变仪；SHPB装置是动态冲击加载的过程(应变率达到102量级)。利用专用测试软件对PCD层厚为1.0 mm、试样2次加载得到的波形图进行分析，得到试样的应力−应变曲线(见图7)。PDC侧压能及单位时间内吸收的侧压能与 PCD层厚度关系曲线如图8所示。

在冲击加载条件下，PCD层厚度不同，PDC抗侧压强度亦不同。从图8可以看出：PCD层越厚，PDC侧压强度越小，而前、后2次加载所测得侧压强度的差异则越大，也就是说，PCD层越厚，损伤对 PDC侧压强度的影响越明显。PCD层厚度从0.5 mm增加到2 mm，PDC侧压强度下降37%，而前、后2次加载得到的侧压强度差却提高了近8倍。

图9所示为试样前、后2次加载的断口形貌。从图9可以发现：PCD层厚度越大，单位时间内吸收的侧压能越少，而前、后2次加载单位时间内平均侧压能的差值则越大；当PCD层厚度h≤1.0 mm时，2次冲击均未引起PCD的整体脱层，但2次冲击引起的试样破坏均较严重；当h=0.5 mm时(图9(a))，由于PCD层过薄，冲击荷载使PCD层破坏之后，瞬间作用于基体，导致基体较大范围崩裂，这是h=0.5 mm的试样比h=1.0 mm的试样破坏更为严重的主要原因；而当h≥1.5 mm时，第2次冲击加载直接引起PCD层崩裂和脱层，说明第1次冲击加载在试样内部引起的损伤极为严重。显然，PCD层厚度越大，损伤对PDC侧压强度的影响越明显。

2 PDC 侧压强度与热残余应力关系

一般认为，PCD层热残余应力是导致PDC非正常失效的主要原因[11−14]。而PCD层与硬质合金基体的热胀系数及弹性模量等物性差异是产生内部热残余应力的主导因素[15]。建立如图 10所示计算模型，取应力松弛温度为1 000 ℃[16]，室温为20 ℃，利用有限元方法，可以计算得到h=1.5 mm时，PCD层内部的热残余应力分布图，结果如图11所示。可见：径向最大拉应力分布于PCD层表面的外径边缘，为295 MPa；而轴向最大拉应力分布于PCD层界面的外径边缘，达到了792 MPa。

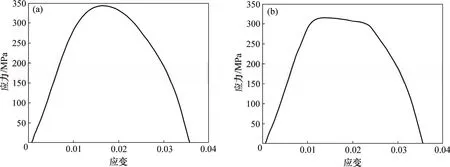
图7 SHPB加载得到的试样应力−应变曲线(h=1.0 mm)Fig.7 Variation curves of stress with strain in dynamic load while h is 1.0 mm

图8 试样侧压能与PCD层厚度关系Fig.8 Relationship between edgewise compressive energy and thickness of PCD layer

图9 SHPB二次加载后试样破坏断口形貌Fig.9 Failure models of PDC in dynamic load

图10 有限元计算模型示意图Fig.10 Geometry of PDC used in numerical simulation

图11 PCD层应力分布云图Fig.11 Stress distribution in PCD layer

保持PDC总厚度13 mm不变，改变PCD层厚度h，PCD层径向和轴向最大应力与h的关系曲线见图12。实践证明，压应力的存在有利于PDC使用过程中抵抗外力，而拉应力的存在对脆性材料则非常有害。显然，随着h的增加，径向压应力逐渐减小，而轴向拉应力则迅速增大。PDC受侧压引起的损伤及其侧压强度与热残余应力相关。热残余应力越大，PDC受冲击侧压后引起的损伤越明显，PDC侧压强度越小。

显然，对同种PDC，加载速率越高，其侧压强度越高，前、后2次加载得到的侧压强度差异越大。另一方面，试样PCD层厚度的提高，会使PDC侧压强度降低，冲击加载引起的破坏越严重。载荷在PDC内部引起损伤，使得PDC抗冲击能力下降。实验结果表明：加载速率越高，PCD层越厚，由冲击载荷引起的PDC内部损伤就越严重。PCD层为PDC钻头的工作层，增加PCD层的厚度可以大幅度地提高PDC的耐磨性，但高热残余应力和易损伤性使PDC的抗冲击能力大大降低。显然，平界面结构的PDC不能单纯依靠提高PCD层厚度来提高使用耐久性，也不适合于二次利用。这一结果对合理设计PDC刀具的几何参数具有重要意义，同时为PDC的二次利用提供了理论和实验依据。

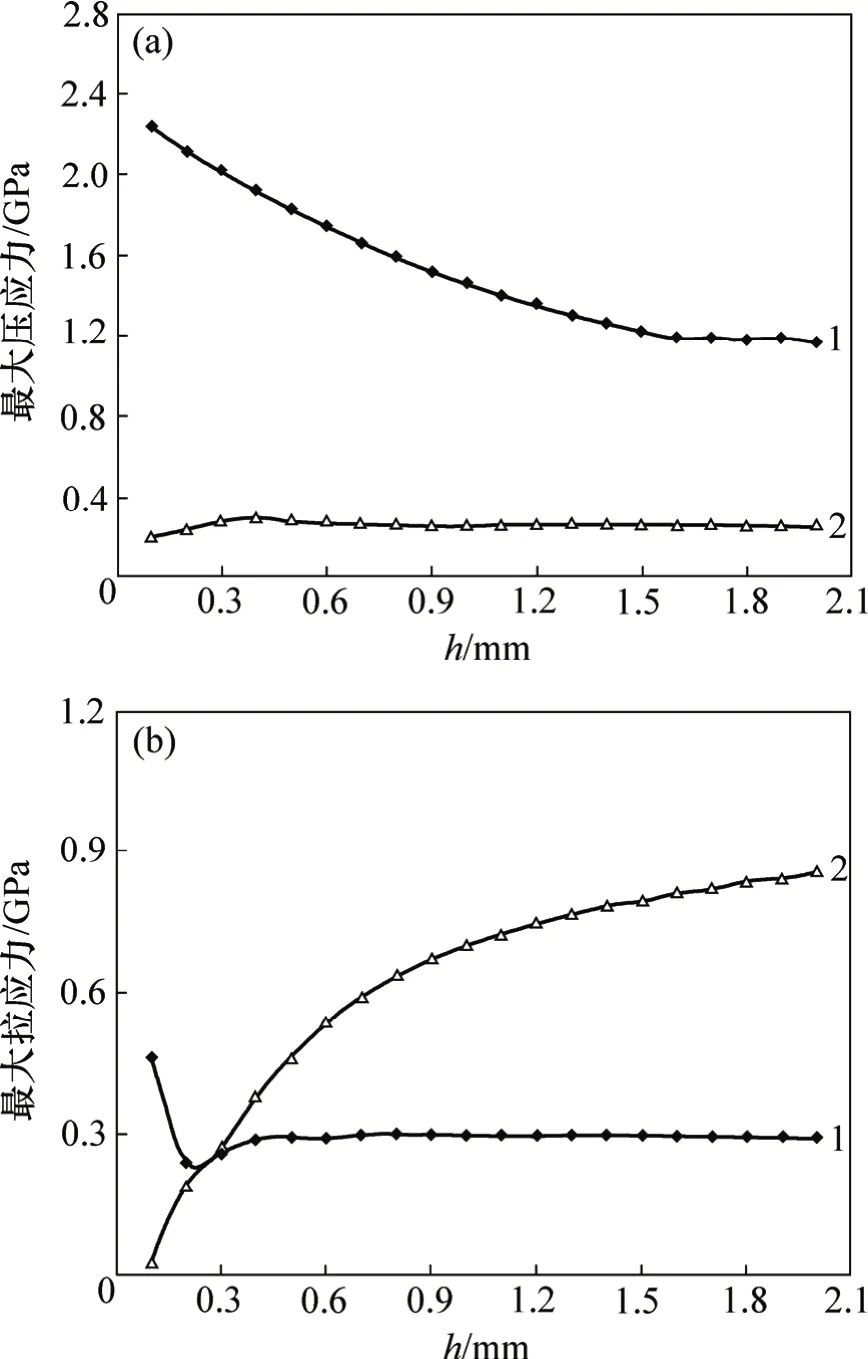
图12 PCD层最大应力与h关系曲线Fig.12 Relationship between maximal stress of PCD layer and h

3 结论

(1) 对同种PDC，加载速率越大，其侧压强度越高，前、后2次加载得到的侧压强度差异越大。在静态加载(10−6m/s)条件下，前、后2次加载得到的侧压强度变化值为0.017 N·m，而准动态(10−2m/s)条件下侧压强度达到1.177 N·m，是静载条件下的70倍。相对于静态加载，在准动态加载条件下，试样单位时间内吸收的侧压能大了4个量级，且前、后2次加载侧压能下降21.2%。另一方面，试样PCD层厚度的提高，会使PDC侧压强度降低，冲击加载引起的破坏也越严重。在冲击加载条件下，PCD层厚度从0.5 mm增加到2 mm，PDC侧压强度下降37%，而前、后2次加载得到的侧压强度差却提高近8倍。

(2) 载荷在PDC内部引起损伤，使得PDC抗冲击能力下降。实验结果说明：加载速率越高，PCD层越厚，由冲击载荷引起的PDC内部损伤就越严重。当PCD层厚度h≥1.5 mm时，第2次冲击加载直接引起PCD层的崩裂和脱层。PCD层为PDC钻头的工作层，增加PCD层的厚度虽然可以大幅度地提高PDC的耐磨性，但高热残余应力和易损伤性使PDC的抗冲击能力大大降低。显然，平界面结构的PDC不能单纯依靠提高PCD层厚度来提高使用耐久性，也不适合于二次利用。这一结果对合理设计PDC刀具的几何参数具有重要意义，为PDC的二次利用提供了理论和实验依据。

[1] Zeren M, Karaqoz S. Sintering of polycrystalline diamond cutting tools[J]. Materials and Design, 2007, 28(3): 1055−1058.

[2] 杨丽, 陈康民. PDC钻头的应用现状与发展前景[J]. 石油机械,2007, 35(12): 70−72.YANG Li, CHEN Kang-min. Application status and development trends of PDC bit[J]. China Petroleum Machinery,2007, 35(12): 70−72.

[3] ZHANG Xiao-fu, LU An-xian, WANG Yu. New vitrified bond diamond grinding wheel for grinding the cylinder of polycrystalline diamond compacts[J]. Journal of Material Science and Technology, 2007, 23(5): 672−676.

[4] GONG Sheng-wu, ZHAO Fu-jun. Failure analysis of polycrystalline diamond compact cutters for breaking rock by bending waves theory[J]. Journal of Central South University of Technology, 2008, 15(1): 112−116.

[5] 张绍和, 鲁凡. 金刚石钻头参数设计规律[J]. 中南大学学报:自然科学版, 2004, 35(2): 195−200.ZHANG Shao-he, LU Fan. Designing method about parameters of impregnated diamond bit[J]. Journal of Central South University: Science and Technology, 2004, 35(2): 195−200.

[6] 李国安, 宋全胜. 聚晶金刚石复合片(PDC)钻头的失效分析[J].华中科技大学学报, 2002, 30(1): 62−64.LI Guo-an, SONG Quan-sheng. The analysis of failure of PDC well bits[J]. Journal of Huazhong University of Science and Technology, 2002, 30(1): 62−64.

[7] Clark I E. The use of polycrystalline diamond (PCD) for machining highly abrasive workpiece materials [J]. Key Engineering Materials, 1996, 118(19): 221−232.

[8] 常领, 陈华忠. PDC钻头在胜利油田深井钻井中的应用[J]. 石油钻探技术, 2007, 35(4): 92−93.CHANG Ling, CHEN Hua-zhong. Application of PDC bits to deep wells in Shengli oilfield[J]. Petroleum Drilling Techniques,2007, 35(4): 92−93.

[9] 刘文建. 霍普金森杆在复合材料动态测试中的应用[J]. 纤维复合材料, 2005, 44(2): 44−46.LIU Wen-jian. Application of Hopkinson Bar in the dynamic test of composites[J]. Fiber Compsites, 2005, 44(2): 44−46.

[10] 肖建清, 陈枫, 徐根. 加载速率与加载波形对混凝土抗拉强度的影响[J]. 土工基础, 2005, 19(4): 70−72.XIAO Jian-qing, CHEN Feng, XU Gen. Influences of loading speed and loading waves on the tensile strength of concrete[J].Soil Engineering and Foundation, 2005, 19(4): 70−72.

[11] CAO Pin-lu, LIU Bao-chang, YIN Kun. Optimization design and residual thermal stress analysis of PDC functionally graded materials[J]. Journal of Zhejiang University: Science, 2006, 7(8):1318−1323.

[12] Bertaqnolli K E, Vale R. Understanding and controlling residual stresses in thick polycrystalline diamond cutters for enhanced durability[C]//An International Technical Conference on Diamond, Cubic Boron Nitride and their Applications.Vancouver, 2000: 1−9.

[13] Paggett J W, Drake E F, Krawitz A D. Residual stress and stress gradients in polycrystalline diamond[J]. International Journal of Refractory Metals & Hard Materials, 2002, 20(3): 187−194.

[14] HUANG Zi-qian, HE Yue-hui, CAI Hai-tao, et al. Thermal residual stress analysis of diamond coating on graded cemented carbides[J]. Journal of Central South University of Technology,2008, 15(1): 165−169.

[15] Lin T P, Hood M, Cooper G A. Residual stresses in polycrystalline diamond compacts[J]. J AM Ceram Soc, 1994,77(6): 1562−1568.