盾构输水隧洞复合衬砌计算模型

杨钊 ，潘晓明 ，余俊

(1. 同济大学 地下建筑与工程系，上海，200092；2. 同济大学 岩土及地下工程教育部重点实验室，上海，200092；3. 中南大学 土木建筑学院，湖南 长沙，410075)

在盾构隧道中，在大数多情况下，二次衬砌不作为隧道结构的主要受力构件，其主要目的是修正施工“蛇行”、运行减糙、提高外管片耐久性和防水等维护作用，盾构隧道复合衬砌的内力计算在设计中一直没有受到重视。近年来，我国拟采用盾构法修建多条大型输水隧洞和城市大型下水管道，二次衬砌在输水隧洞中将作为主要受力构件出现。因此，研究盾构隧洞复合衬砌计算模型已成为一项重要的课题。现有的盾构隧洞复合衬砌计算模型多基于国际隧道协会发布的盾构隧道衬砌设计指南[1]。在设计指南中提出了 2种盾构隧洞复合衬砌计算模型：双层框架模型和弹性方程模型。张厚美等[2]改进了第 1种模型中内、外层衬砌接触界面模型，提出了关于接触界面的3种模型：抗压缩模型、局部抗弯模型和剪压模型。以上模型均是基于荷载－结构法，没有考虑土体开挖、回填注浆等施工过程对衬砌结构受力的影响。章青等[3]基于非连续介质变形理论提出了一种新的模型，模型通过放松离散单元交界面上的位移连续条件，来模拟螺栓连接和各种缝面的不连续变形特征。该模型仿真性强，计算效率高。本文作者从理论上分析双层框架模型存在的不完善之处，提出一种基于地层−结构法的计算模型即实体叠合计算模型。该模型不仅能更精确地考虑土体与管片的相互作用，而且能考虑隧洞施工的各个阶段对结构受力的附加影响。

1 双层框架模型

1.1 受力叠加模型

考虑到外管片与内衬不是同期施工，且施工期和运营期的受力状况不同，将衬砌的受力过程分成3种工况。

工况 1：外管片施工期，管片自重、施工期荷载及全部水土压力由外管片环单独承担。

工况 2：运营初期，此时外部水土压力已经达到稳定，且全部由外管片环承担。内衬和外管片共同承担内水压力和内衬自重作用。

工况 3：运行稳定期，内衬和外管片共同承担工况2后继增大的外部水土压力。

由于工况3不为设计控制工况，双层框架模型在控制工况下的受力模型如图1所示。在模型中，外管片的最终受力、变位状态由工况1与工况2的受力、变位状态叠加而得。由图1可知，双层框架模型存在1个假定：工况1管片的受力与变位状态不影响工况2管片和内衬的受力与变位，即外管片已发生的变形与受力对管片与内衬二者相互作用无影响。这一假定只有在管片接头刚度、管片、内衬混凝土、管片周围土体抗力均为线弹性以及管片周围地基弹簧的分布范围不变的情况下才能成立。而在实际工程中，管片接头的抗弯刚度是非线性的，在不同工况下管片周围地基弹簧分布范围是变化的，管片、内衬混凝土、管片周围土体抗力只能近似地看着是线弹性的。

1.2 接触界面模型

在双层框架模型中，管片与内衬接触界面的力学行为可通过在接触界面处设置压缩弹簧、压缩剪切弹簧或刚性链杆来实现。

考虑 2根长度为l的Euler-Bernouli叠合梁[4−5]，弹性模量为E，截面弯曲惯性矩为I。假定2根梁的接触界面之间只能传递接触压力，而不能传递弯矩与剪力。2根梁的接触界面之间分别采用压缩弹簧和goodman接触单元来模拟接触界面的接触力学行为。

把梁用1个二节点的梁单元模拟。采用压缩弹簧模拟界面力学效应，设压缩弹簧的刚度系数为K，则压缩弹簧单元对整个体系的附加刚度矩阵为：

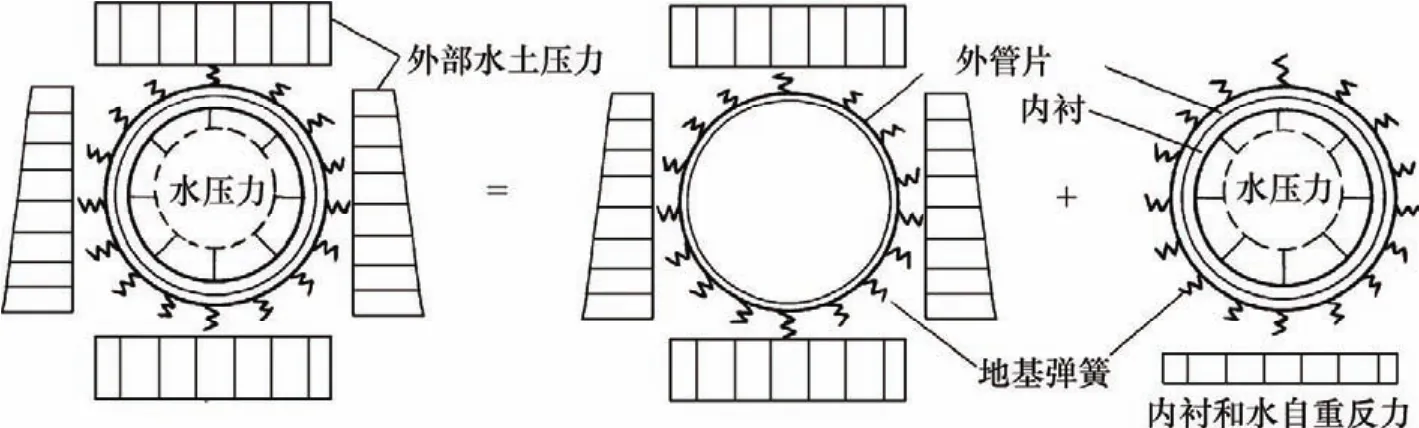
图1 双层框架受力叠加模型Fig.1 Superposition model of double linings under loading

在界面之间设置只能传递压力、不能传递剪力的goodman接触单元，接触单元上缘与下缘的垂直位移差可以表示为[6]：

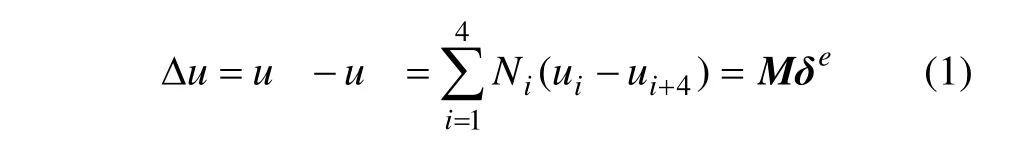
式中：

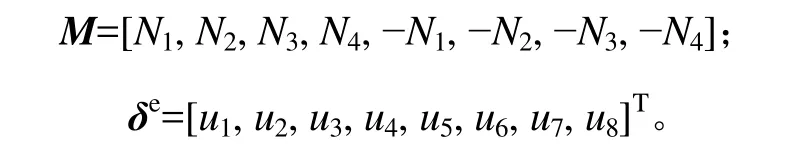
单元内正应力与垂直位移差成正比，即

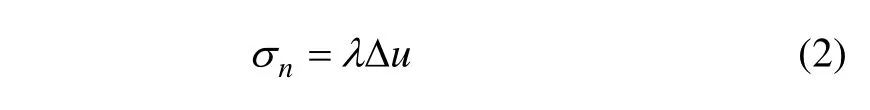
假定单元各结点上产生虚位移δ*e，那么，单元内虚位移差为：

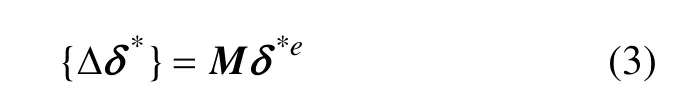
在单位长度上，单元应力所做虚功为：

沿单元长度积分后，即得到单元应力所做的虚功，等于单元结点力所做的虚功，由此可得接触单元的刚度矩阵(即为接触单元对整个体系的附加刚度矩阵)为：

2种附加刚度矩阵只有在梁单元转角为0°或梁单元长度足够小，且梁单元两节点的位移相等时，两者的刚度矩阵利用K弹簧=0.5λtl换算，得到的计算结果才是完全等同的。

同理可以得到压剪弹簧也只有在接触界面划分足够多单元的情况下，才能较为精确地模拟2根梁之间的真实接触状态。

对于复合衬砌结构，第1阶段由外管片承受外周水、土压力，第2阶段由内衬与外管片共同承担内水压力、内水与内衬自重。因此，复合衬砌结构可看作2个阶段受力的叠合梁结构。现考虑一阶段受力叠合梁，叠合梁由2根截面属性与材料属性均一样的Euler-Bernouli梁组成，梁的弹性模量为2.0 GPa，截面尺寸为1 m×1 m，梁的长度为20 m，梁的一端固定，另一端承受集中力荷载10 kN。假设2根梁之间的接触界面通过设置锚筋，表面凿毛等方式使得2根梁在界面之间可以传递弯矩与剪力并保持界面之间的位移协调。若采用双层框架模型计算，则应在2梁之间设置刚性链杆来模拟这种接触界面性质。有限元模型如图2所示。在实际计算过程中，可以将通过上述界面处理的2根梁看作1根整体梁进行计算。

当采用刚性链杆模拟界面力学性质，可以实现 2根梁在接触界面间的位移协调。采用双层框架模型计算所得梁的挠度与采用整梁计算所得的挠度相近，双层框架模型计算所得最大挠度值为1.59 cm；整体梁模型计算所得最大挠度值为1.50 cm。但2种模型计算所得的梁端最大弯矩与采用整梁计算所得的最大弯矩值相差甚远。采用双层框架模型计算得到梁截面的最大弯矩为4.11×105N·m；将梁截面作为一个整体，计算所得梁截面最大弯矩为1.98×106N·m。这主要是因为当采用双层框架模型计算时，上梁与下梁均具有中性轴，位于上梁与下梁的截面形心处，而实际上中性轴只有1条位于整体梁的截面形心处，这与实际情况不符。

在 ABAQUS中，双层框架模型不精确模拟一阶段受力叠合梁，更不可能精确模拟受力更加复杂的二阶段受力叠合梁。因此，当采用 ABAQUS数值模拟软件计算时，复合衬砌计算模型应采用实体单元模型。

2 实体叠合模型

2.1 模型基本假定

隧道衬砌结构沿隧道纵向可以认为是一个无限长的结构体，在不考虑纵向变形的条件下，管片环的内力不沿纵向发生变化，因此，在计算过程中，可以将每一环管片作为一个平面应变状况考虑。

图2 有限元模型Fig.2 Model of FEM

2.2 围岩结构有限元模拟

在实体叠合模型中采用地层−结构法计算管片、内衬的受力与变位，考虑到土体材料的弹塑性，选用Drucker-Prager屈服准则和相关联流动法则来模拟土体材料的非线性应力−应变特性。

工程实践与理论研究表明[7−8]：当隧道上覆土层为砂性土时，采用水土分算，水压力直接作用于管片上，土体的容重采用浮容重计算，土体的侧压力系数取为k0。

2.3 实体简化接头模型

2.3.1 模型简介

当管片采用梁单元模拟时，其纵向接头的力学性能可采用旋转弹簧、压缩弹簧和剪切弹簧来分别模拟接头的抗弯、抗压和抗剪的力学状态[9]。这种“梁−弹簧模型或壳弹簧模型”[10−13]已经被广泛应用于工程设计与计算中，并经过实测验证。当采用试验给定的上述诸接头力学参数后，计算所得的管片截面内力和变位值均能与实测值基本吻合。

当管片采用实体单元模拟时，其接头的力学性能现多采用“接触单元”来模拟[14−15]。根据接头的实际受力与变形情况，管片接头处的接触单元必须综合考虑：弹性密封垫与混凝土管片接触、管片与管片的接触、螺栓与螺栓孔接触以及螺栓的锚固作用，这将使接头处的建模问题显得十分复杂；同时，在国内外众多的接头实验资料中，很少提及管片接头相关的接触参数。这使得管片的接头模型不仅在技术上不易实现，而且在精度上也难以准确保证。为此，本文作者提出了一种新的实体简化接头模型以用于采用实体单元建模的管片分析。本文建议的接头模型既能避免接头部位上的复杂情况，又能借用过去从常规实验所得或直接采用接头刚度理论计算的接头力学参数。实体简化接头模型的示意图如图3所示。

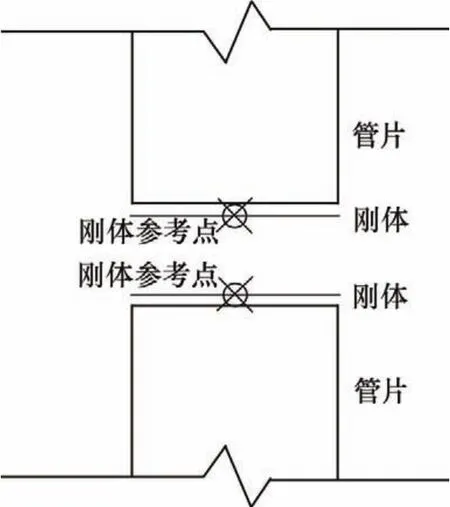
图3 实体简化接头模型示意图Fig.3 Simplified model for solid element

在模型中将接头端肋与刚性体相连，并设置刚性体的参考点位于管片截面形心处。在两刚性参考点之间设置剪切弹簧、压缩弹簧和抗弯弹簧来模拟接头的力学性质，这 3根弹簧的刚度取用“梁−弹簧模型或壳弹簧模型”中对应的弹簧刚度。

2.3.2 模型验证

分别采用实体简化接头模型与“梁−接头模型”计算如图4所示模型。AB边上受到400 kN/m的均布荷载，BC边上受到300 kN/m的均布荷载。在AD和DC边分别施加沿X和Y轴的对称边界条件。洞室外直径为7.0 m，管片厚度为40 cm。洞室由4片管片组成，管片接头分别位于 0°，90°，180°和 270°。0°角和90°角分别位于X轴正方向和Y轴正方向。

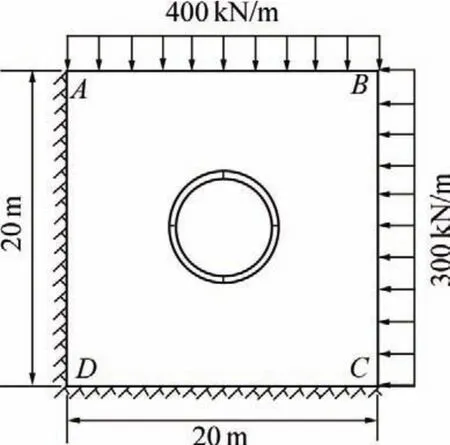
图4 模型示意图Fig.4 Simplified plot of model

分别采用实体单元与梁单元模拟管片，将两者计算所得的管片内缘环向应力对比，如图5所示。采用接头模型计算所得的管片内缘环向应力相对误差小于5%，实体简化接头模型能有效地应用于工程实际计算。

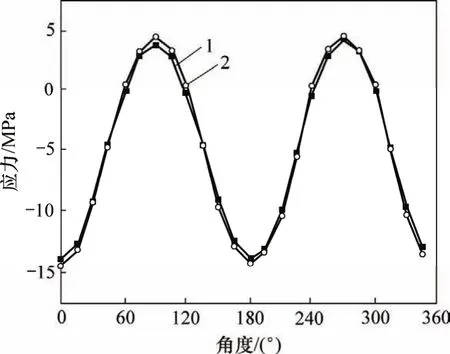
图5 管片内缘环向应力对比Fig.5 Comparisons of circumferential stress between beam element and solid element

2.4 管土接触模型

地层与管片之间采用无厚度的接触单元模拟。接触面的径向力学行为采用“硬接触”模拟，即接触面之间可以传递无穷大的径向压应力，但不能传递径向拉应力(在径向拉力的作用下接触面自动脱开)。接触面的切向力学行为采用库仑摩擦模型模拟[6]。库仑摩擦模型用于判断接触面时是否发生相对错动，同时也用于分析相对滑动对管片衬砌应力场的影响。

库仑摩擦模型可以定义如下：

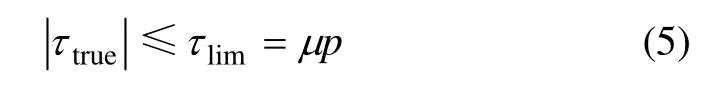
式中：τtrue为计算所得的真实剪应力；τlim为最大允许剪应力；μ为接触界面综合摩擦因数；p为接触面法向压力。在接触计算中，接触面之间传递的最大剪应力不得超过接触压力乘以库仑摩擦因数。当计算所得的剪应力大于接触压力乘以库仑摩擦因数时，接触面发生相对滑动，将接触界面的状态设为滑移进入下一步迭代计算。

2.5 复合衬砌的接触界面模型

复合衬砌接触界面模型与内、外层衬砌间接触界面的处理方式有关。根据接触界面处理方式的不同，提出4种接触界面模型。

2.5.1 无黏聚力模型

内衬施工前将管片内表面的螺栓手孔、注浆孔、起吊孔等凹槽用水泥充填抹平，然后浇注内衬混凝土。此时，内外层衬砌之间可以传递径向压力，且可以通过摩擦力的形式传递切向剪力。复合衬砌接触界面模型采用与管土接触相同的库仑摩擦模型。

2.5.2 有黏聚力模型

浇筑内衬前抹平外管片内表面较大凹槽，其余部分通过凿毛处理。此时，内、外层衬砌间可以传递压力，且可以通过黏聚力与摩擦力的形式传递剪力。接触面的径向力学行为采用“硬接触”模拟。接触面的切向力学行为采用有黏聚力的库仑摩擦模拟。

有摩擦的库仑模型可以定义如下：

式中：τtrue为计算所得的真实剪应力；τlim为最大允许剪应力；μ为接触界面综合摩擦因数；c为新老混凝土之间的黏聚力；p为接触面法向压力。

2.5.3 位移协调模型

在管片预制时设置锚筋孔，内衬浇筑时，在管片锚筋孔处设置锚筋，锚筋伸入到内衬混凝土内，并与内衬受力钢筋点焊连接。此时，内、外层衬砌界面之间的位移可以认为是协调的，接触界面模型采用位移协调模型。

2.5.4 局部位移协调模型

内衬混凝土或钢筋伸入外管片手孔或凹槽中，这些部位的接触界面的位移可以认为是协调的。其余部位应接触界面的处理方式选用无黏聚力模型或有黏聚力模型。

2.6 实体叠合模型计算过程

为了考虑内衬施作之前外管片先已发生的变形与受力、对后续管片与内衬二者相互作用的附加影响，计算中应需计入外管片、内衬结构二者先后的不同受力作用。即在管片参与内衬结构共同受力时，要先计入已经发生的管片内力与内净变形的收敛值。

在数值模拟分析计算过程中，可以采用以下步骤来考虑并计入外管片和内衬的实际受力及其变形状态：(1) 建立有限元数值模型；(2) 平衡初始地应力；(3) 开挖土体单元，并施作外层管片；(4) 施加外水压和管片自重；(5) 输出按此时模型计算所得各单元的应力以及外层管片的变位值；(6) 输入上面输出的应力，用以平衡原先应力。此时的受力状态为：土体已开挖，外层管片已经施作，外周土水压力作用在管片上。经过应力平衡后，此时土体与外层管片的“计算变形”为0，应力状态为第5步输出的应力状态，即为二次衬砌施作之前的真实受力状态。(7) 施作二次复合衬砌的内衬；(8) 施加内水压和二衬自重；(9) 输出此时的应力状态，即为真实的二衬复合衬砌受力状态。输出此时外层管片的变位值，并使之与第5步管片变位的输出值相迭加，即为真实状态下管片的变位值。

当物体处于小变形状态时，其名义应变等于真实应变。因此，管片平衡应力后的应变(第9步输出的应变)应即等于管片的真实应变减去管片平衡前的应变值(第5步输出的应变)，进而得出管片的真实变位值，其值可分解为平衡应力前的变位值(第 5步输出的变位值)再加平衡后的变位值(第9步输出的变位值)。因土体的塑性状态是通过应力判断，应力是通过增量应变计算，因此经过第6步的平衡应力后，土体的应力状态与塑性区与实际状态相符。

3 工程实例

青草沙原水过江隧洞工程位于上海长江隧道下游约80 m处，浦东侧越江点在五号沟，长兴岛越江点在该岛新开河附近，全长7.23 km。越江输水管道设计拟采用 TBM 施工，采用有压输水，设计为圆形断面，衬砌结构外直径为6.8 m，管片厚为400 mm，内衬厚为 250 mm。隧道设计的控制截面上覆土为砂性土，覆土高度为 10.5 m，隧道中心线处内水压为 0.309 MPa，隧道中心线处外水压为0.300 MPa。内、外层衬砌间采用20 cm×20 cm分布的锚筋，故复合衬砌接触界面模型采用位移协调模型计算。

有限元计算范围为盾构隧道左右各取30 m，地表往下取45 m。对边界，假设左右两侧存在水平约束，下部存在竖向约束，上部边界自由。有限元计算模型如图6所示。纵向接头的正、负抗弯、抗压、抗剪刚度系数分别取为：kθ+=4.0×107N/(m·rad)，kθ-=2.0×107N/(m·rad)，Kn=5.0×1012N/m，KT=5.0×1011N/m。管片的压缩模量E和泊松比μ取为：E=3.55×104MPa，μ＝0.2；内衬混凝土的弹性参数取为：E=3.25×104MPa，μ＝0.2。土层参数见表1。

图6 有限元模型Fig.6 Model of finite element method

表1 土层参数Table 1 Parameter of soil layer

4 计算结果分析

根据上述计算模型，采用 ABAQUS有限元软件实现青草沙原水过江隧洞控制截面计算。采用实体单元计算时，可以通过预先定义截面得到管片与内衬的内力，但在后处理中无法图形显示内力。将内力与变位值输出，编制后处理程序得到结构的内力图与变位图。

图7所示为管片变位矢量。由图7可知：内水压施加以后，管片竖直方向压缩，垂直方向伸长。管片的形状由原先的圆形变成扁平的椭圆形。

图8所示为管片截面内力。由图8可见：弯矩以管片内侧受拉为正。管片弯矩的峰值出现在管顶、管底和两腰，其管顶、管底为正值，两腰弯矩为负值。最大正弯矩位于管底处，其值为1.10×105N·m。最大负弯矩位于管腰处，其值为−0.87×105N·m。设轴力以受拉为正，受压为负。管片全截面受压。管顶、管底轴压力小，而管腰轴压力大。轴压力最大值位于管腰处，最大为6.57×105N。

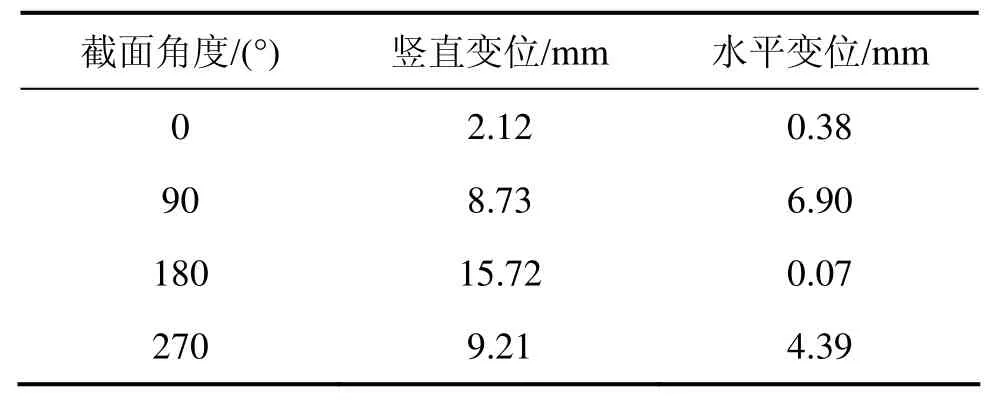
表2 管片控制截面变位Table 2 Displacement of segment in control section

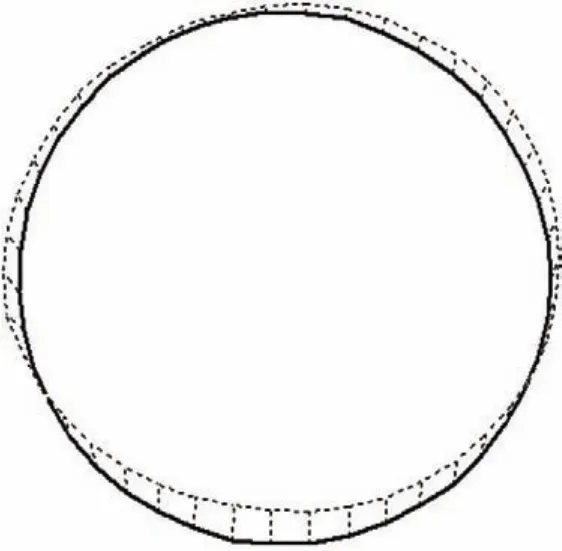
图7 管片变位矢量Fig.7 Displacement vector diagram of segment

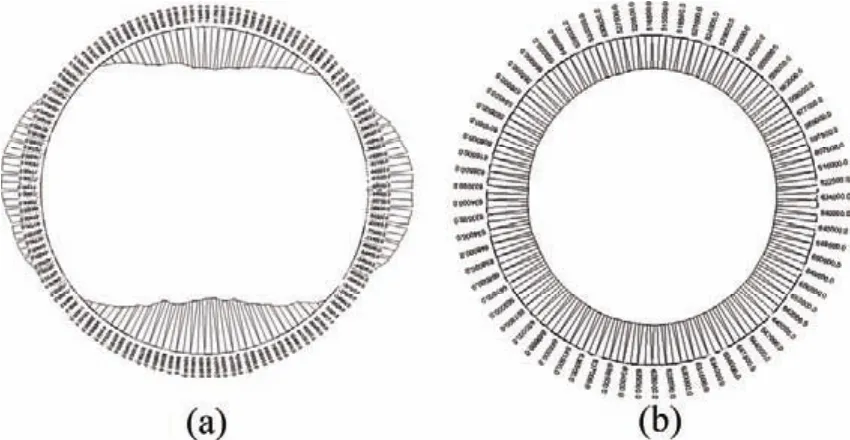
图8 管片截面内力Fig.8 Member force of segment section

内水压施加以后，由于内衬质量与内水的质量，内衬主要发生向下的刚体位移，如图9所示。

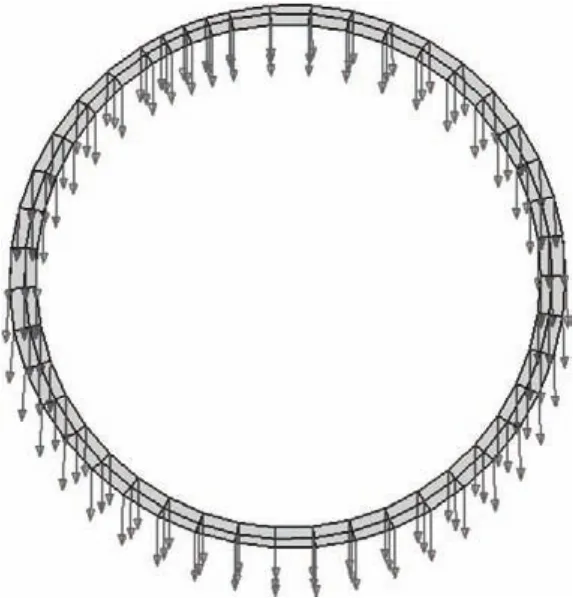
图9 内衬变位矢量Fig.9 Displacement vector diagram of second linings

图10所示为内衬截面内力。由图10可见：弯矩以衬砌内侧受拉为正。内衬弯矩的峰值出现在内衬顶部、内衬底部和两腰，内衬顶部、底部为正，两腰为负。最大正弯矩位于内部底部，为1.32×104N·m。最大负弯矩位于内衬腰处，其值为−0.97×104N·m。内衬全截面受拉。内衬顶部、底部轴拉力大，而腰部轴拉力小。轴拉力最大值位于内衬底部，最大值为−4.56×105N。

图10 内衬截面内力Fig.10 Member force of seconding linings section

运营期内水压作用，内、外衬砌联合承担内水压力引起轴拉力。研究内、外衬砌对轴拉力的贡献(见表3)，对以后类似的工程有重大意义。当内水压力作用时，内衬产生轴拉力，外衬轴力减小。因此，可以认为：内水压力作用产生轴拉力=内衬轴拉力+外衬轴力减少量(其中，外衬轴力减小量=施工期外管片轴力−运营其管片轴力)。

内、外层衬砌轴力对比如表3所示。由表3可知：内水压力引起的衬砌总拉力约40%由内衬承担。

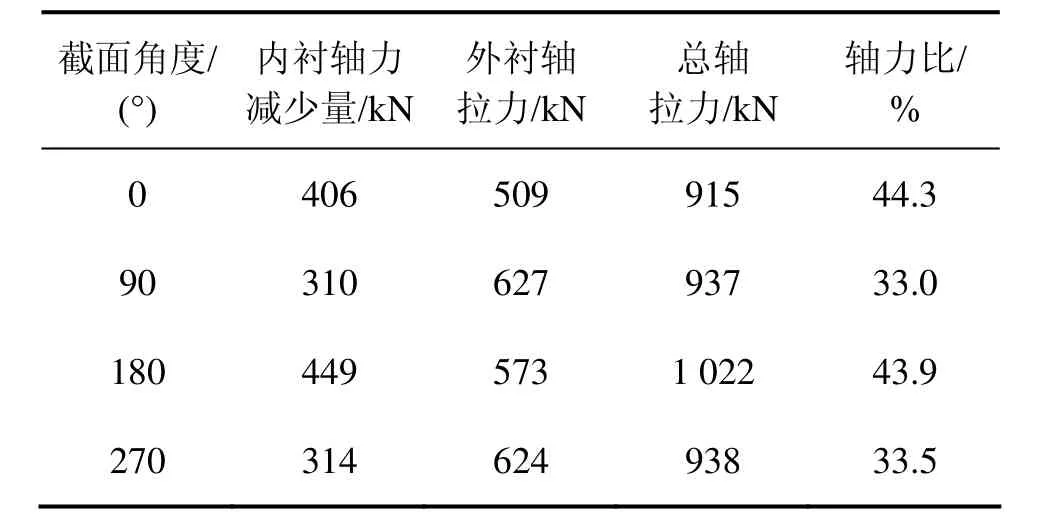
表3 内、外层衬砌轴力对比Table 3 Comparison of axial force on primary and seconding linings

5 结论

(1) 双层框架模型的接触界面处理不能精确模拟内、外层衬砌间界面的力学行为，且不能考虑外管片先已发生的受力与变形对后续内、外衬砌之间相互作用的影响。

(2) 实体叠合模型内、外层衬砌接合面力学性态采用传统的接触单元模拟，理论体系清晰，能真实、准确地反映接触界面的力学性态。

(3) 实体简化接头模型参数物理意义明确，参数可通过常规试验或接头刚度计算理论确定。该模型不仅简化了当管片采用实体单元建模时接头部位处理的复杂性，而且能有效地保证计算的精度。

(4) 实体叠合模型不仅可考虑隧洞施工的各个阶段对结构受力的影响，而且能较好地反映外管片已发生的变形与受力、对管片与内衬二者相互作用的附加影响。实际工程应用结果表明：实体叠合模型对于分析盾构隧洞复合衬砌结构是可行且有效的。

[1] Takano Y H. Guidelines for the design of shield tunnel lining[J].Tunneling and Underground Space Technology, 2000, 15(3):303−331.

[2] 张厚美, 过迟, 吕国梁. 盾构压力隧洞双层衬砌的力学模型研究[J]. 水利学报, 2001(4): 28−34.ZHANG Hou-mei, GUO Chi, LU Guo-liang. Mechanical model for shield pressure tunnel with secondary linings[J]. Journal of Hydraulic Engineering, 2004(4): 28−34.

[3] 章青, 卓家寿. 盾构式输水隧洞的计算模型及其工程应用[J].水利学报, 1999(2): 19−22.ZHANG Qing, ZHUO Jia-shou. A computational model of shield tunnel for water conveyance[J]. Journal of Hydraulic Engineering, 1999(2): 28−34.

[4] 冯紫良. 杆系结构的计算机分析[M]. 上海: 同济大学出版社:1991: 50−79.FENG Zhi-liang. Trussing structure computer analysis[M].Shanghai: Tongji University Press, 1991: 50−79.

[5] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2006:128−173.WANG Xu-cheng. The finite element method[M]. Beijing:Tsinghua University Press, 2006: 128−173.

[6] 朱伯芳. 有限单元法原理与应用[M]. 北京: 中国水利水电出版社, 2004: 72−156.ZHU Bo-feng. The finite element method theory and application[M]. Beijing: China Water Power Press, 2004:72−156.

[7] 钟登华, 佟大威, 王帅, 等. 深埋 TBM 施工输水隧洞结构的三维仿真分析[J]. 岩土力学, 2008, 29(3): 609−613.ZHONG Deng-hua, TONG Da-wei, WANG Shuai, et al. 3D simulation analysis of structure of deep water diversion tunnel with TBM constructing[J]. Rock and Soil Mechanics, 2008,29(3): 609−613.

[8] Msdhimo H, Ishimura T. Evaluation of the load on shield tunnel lining in gravel[J]. Tunneling and Underground Space Technology, 2003, 18(2): 233−241.

[9] ZHU He-hua, Hashimoto T. Back-analysis for shield tunnel using beam-joint model[R]. Shanghai: Tongji University.College of Civil Engineering, 1996.

[10] 朱合华, 丁文其, 李晓军. 盾构隧道施工力学性态模拟及工程应用[J]. 土木工程学报, 2000, 33(3): 98−103.ZHU He-hua, DING Wen-qi, LI Xiao-jun. Construction simulation for the mechanical behavior of shield tunnel and its application[J]. China Civil Engineering Journal, 2000, 33(3):98−103.

[11] 朱伟, 黄正荣, 梁精华. 盾构衬砌管片的壳−弹簧设计模型研究[J]. 岩土工程学报, 2008, 28(8): 940−947.ZHU Wei, HUANG Zheng-rong, LIANG Jing-hua. Studies on shell-spring design model for segment of shield tunnel[J].Chinese Journal of Geotechnical Engineering, 2008, 28(8):940−947.

[12] 苏宗贤, 何川. 盾构隧道管片衬砌内力分析的壳−弹簧−接触模型及其应用[J]. 工程力学, 2007, 24(10): 131−136.SU Zong-xian, HE Chuan. Shell-spring-contact model for shield tunnel segmental lining analysis and its application[J].Engineering Mechanics, 2007, 24(10): 131−136.

[13] 朱合华, 刘庭金. 超浅埋盾构法隧道施工方案三维有限元分析[J]. 现代隧道技术, 2001, 38(6): 14−18.ZHU He-hua, LIU Ting-jin. 3D FEM analysis of shield driven tunnel with super shallow depth[J]. Modern Tunneling Technology, 2001, 38(6): 14−18.

[14] Blom C B M, Host E J, Jovanovic P S. Three-dimensional structural analyses of the shield-driven “Green Heart” tunnel of the high-speed line south[J]. Tunneling and Underground Space Technology, 1999, 14(2): 217−224.

[15] Klotz U, Vermeer P A. A 3D finite element simulation of a shield tunnel in weathered Singapore Bukit Timah Granite[J].Tunneling and Underground Space Technology, 2006, 21:272−283.