中国股票市场金融持续时间的统计特征挖掘

鲁万波

(西南财经大学 统计学院，成都 610074)

中国股票市场金融持续时间的统计特征挖掘

鲁万波

(西南财经大学 统计学院，成都 610074)

文章基于日内交易数据，全面考察了金融持续时间的描述统计规律和分布特征；关注了与日内交易活动密切相关的交易持续时间、价格持续时间和成交量持续时间这几个特征变量的描述统计与无条件分布特征；将金融持续时间分为交易持续时间、价格持续时间和成交量持续时间进行了深入细致的研究。

金融持续时间；日内高频数据；描述统计；非参数密度估计

1 金融持续时间及其特征

用 t表示物理(或日历)上的时间，{ti}i∈{1,2,…}是在某一概率空间（Ω，P）上的非负随机到达时间变量序列，并且随机到达时间满足 0≤ti≤ti+1，则序列{ti}称为[0，∞]上的一个点过程。 如果对任意的 i，ti＜ti+1，则{ti}称为一个简单点过程。 事实上，简单点过程排除了事件同时发生的可能。进一步的，如果用n(t)表示在t∈[0,T]中某事件发生的数目，则tn(T)=T是最后的观测时点，是全部的观测样本，样本容量是。

用xi表示两个连续的事件之间的时间间隔，即

则{xi}i∈{1,2,…}称为与点过程{ti}相关的持续时间过程。

总的来说，有三大类金融持续时间：交易持续时间、价格持续时间和成交量持续时间。各种类型持续时间的获取与点过程的“打薄(Thinning)”有关，所谓打薄指的是从原始数据中提取子集的过程。

交易持续时间是最常见的一种金融持续时间，定义为连续交易之间的时间间隔，可通过买卖报价或交易活动获得。交易持续时间反映交易的活跃程度，与交易强度和流动性需求密切相关。进一步，买卖交易持续时间定义为连续买或卖之间的时间间隔，反映市场上某一方的交易强度和流动性需求。很多学者应用自回归条件持续时间(ACD)模型研究交易持续时间，一些学者侧重关注选择更合适的模型捕捉持续时间的动态变化规律，一些学者侧重关注检验各种各样的市场微观结构假定。比较有代表性的成果可见Engle和Russell(1998)、Jasiak(1998)、Engle(2000)、Zhang,Russell 和 Tsay(2001)、Bauwens 和 Veredas(2004)、Manganelli(2005)和 Bauwens(2006)等的论文。归纳起来，几乎所有的研究发现交易持续时间具有交易聚集(Clustering)特征——长的持续时间之后是长的持续时间，短的持续时间之后是短的持续时间，表明交易聚集阶段有新信息到达；大多数的研究发现交易持续时间具有过度分散(Overdispersed)特征——交易持续时间的标准差大于均值，说明指数分布并不适合于交易持续时间的无条件分布；交易持续时间具有较大的持续(Persisitence)特征——虽然自回归系数的和小于1处于平稳区域但是接近1，似乎为近单位根过程；有的研究发现在研究样本数据中存在大量的零交易持续时间，这与交易系统记录的最小时间有关，给持续时间数据的分析带来一定困难。

价格持续时间是按照价格信息变化对持续时间点过程的打薄获取。假设在交易时刻股票的买卖成交价格为pi，在ti'的成交价格为pi'(i'＜i)，则价格持续时间定义为达到一定价格累积变化的时间。Engle和Russell(1997)给出了获取价格持续时间的规则：如果|pi-pi'|≥dp，则保留原始持续时间序列中的第i(i＞1)个点,第1个点为原始持续时间序列中的第1个点，是dp阈值，为一外生变量，表示价格绝对变化的累积。为了避免买卖价格跳跃 (Bid-ask Bounce)导致的偏差，Engle和Russell(1997，1998)提出运用中间价定义价格持续时间：如果ti在交易时刻某一股票委托订单簿中的最高买入价 (买一)与最低卖出价(卖一)分别为pbi1和pai1，交易价格选用中间价pmi=(pbi1+pai1)/2。由于价格持续时间是价格变化到一定程度所需要的时间，因此价格持续时间与股票价格的即时波动率函数密切相关，可通过价格持续时间对波动率进行建模。相对于交易持续时间和买卖交易持续时间而言，价格持续时间要长一些，在分笔交易数据中，买卖价格跳跃几乎不提供任何信息。Engle 和 Russell(1998)、Bauwens 和 Giot(2000)、Bauwens 和 Veredas(2004)、Fernandes 和 Grammig(2006)等 的研究发现价格持续时间具有正自相关性、过度分散性、形状右偏和明显日内季节性等特征。

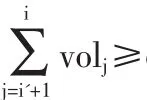
中国股票市场经过近二十年的迅速发展，已经成为仅次于日本、香港的亚洲第三大股票市场，也是目前国际上采取限价委托指令驱动为交易机制的最大的新兴市场之一。作为转轨经济阶段发展起来的新兴证券市场，中国股市具有独特的市场结构，政策市、全民市、博弈市、震荡市与过渡市依然是中国股市的主要特征。那么中国股票市场的金融持续时间具有什么样的统计特征？这对于进一步研究中国股市的微观结构具有重要的现实意义。

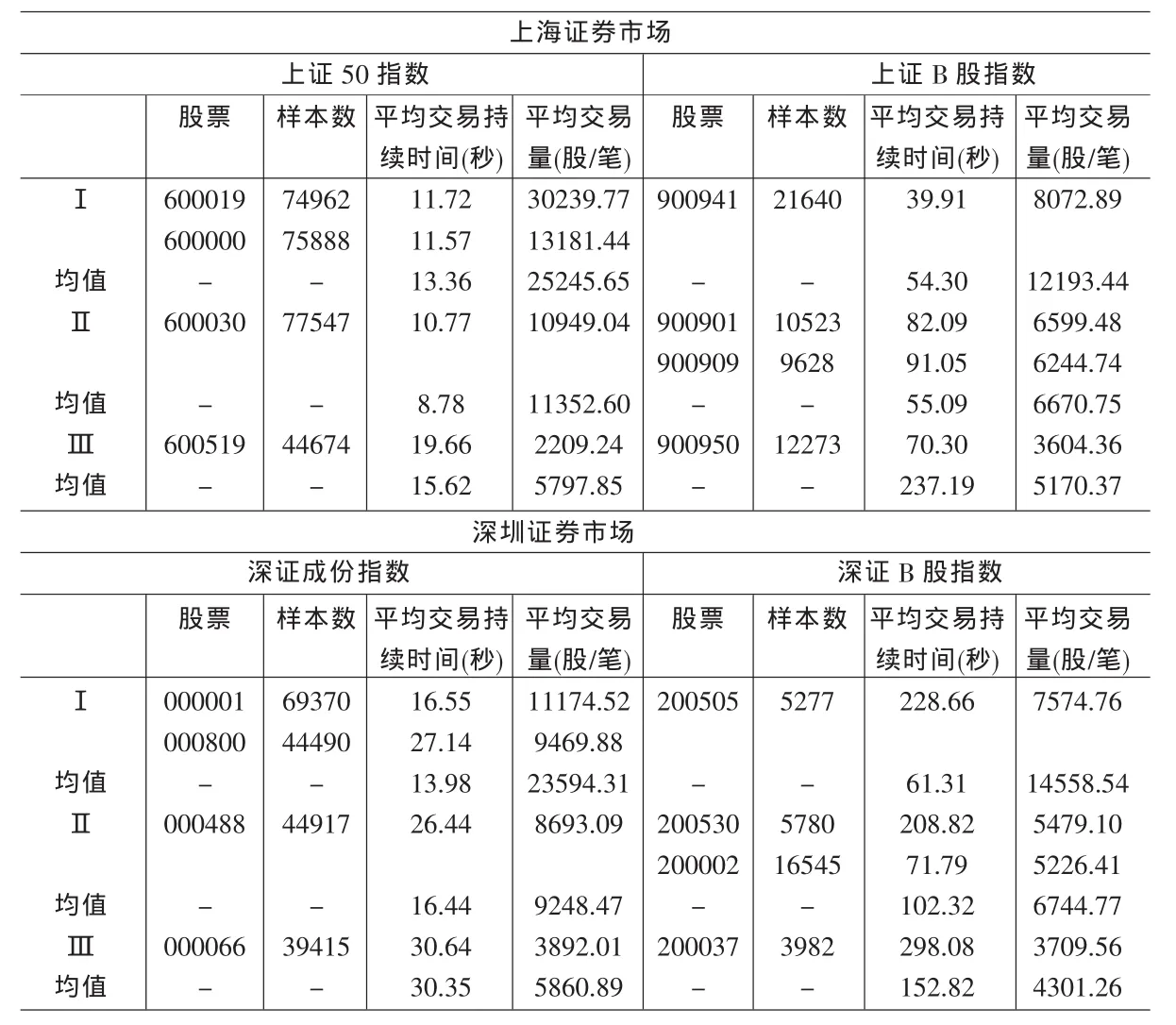
表1 抽样股票的基本信息(2006年8月1日至10月31日)

2 实证研究结果

2.1 研究样本和数据描述

由于交易频繁和交易清淡的股票在交易持续时间的结构上有很大的差异，以下用于实证分析的样本数据除浦发银行(600000)、上电 B股(900901)、深发展 A(000001)和万科 B(200002)外，还在每个样本期间内通过分层随机随机的抽取了12支股票用于分析。首先分别将上证50指数、上证B股指数、深证成份指数、深证B股指数按每笔交易的平均成交量分为三组，依次为交易频繁、中等和清淡，然后随机的在各组中抽取一只股票。抽取的时间分别为2006年8月1日至10月31日，2007年3月1日至5月31日共6个月。在2006年8月1日至10月31日期间，从上证50指数中抽取的股票为宝钢股份(600019)、中信证券(600030)、贵州茅台(600519)，从上证B股指数中抽取的股票为东信B股(900941)、双钱 B股(900909)、新城 B股(900950)，从深证成份指数中抽取的股票为一汽轿车 (000800)、晨鸿纸业(000488)、长城电脑(000066)，从深证B股指数中抽取的股票为珠江B(200505)、大冷B(200530)、深南电B(200037)1。 这样选取的股票能够代表研究样本期内按照交易活跃程度从高到低划分的三种股票类型，抽取股票的基本信息如表1所示。平均来看，交易量越大，交易持续时间越短，说明交易越活跃，Ⅰ类为交易最为活跃的股票，Ⅱ类为交易较为活跃的股票，Ⅲ类为交易最不活跃的股票（见表1）。

2.2 交易持续时间的统计特征

表2给出了2006年8月1日至10月31日期间沪市上证50和上证B股指数各样本股的描述统计结果。从总体上看，上证50指数样本股的平均交易持续时间明显小于上证B股指数样本股，上证50指数样本股交易持续时间的标准差明显小于上证B股指数样本股，这说明上证50指数样本股的交易强度和流动性明显大于上证B股指数样本股，且上证B股指数样本股的交易活动发生较为分散。就交易持续时间的分布特征而言，我们明显地观察到过度分散性(变异系数均大于1)，也就是说标准差均大于均值，这说明指数分布拟合交易持续时间的分布是不合适的。所有样本股的偏度均大于零，峰度均大于3，这说明交易持续时间的分布应该是正偏、尖峰的。比较而言，上证B股指数样本股的变异系数大约是上证50指数样本股的2倍。各股票交易持续时间的LB检验统计量的数值均远远大于5%的显著水平下的检验临界值(30)=43.773，表明具有明显的自相关性。为节约篇幅，图1给出了浦发银行(600000)交易持续时间的核密度估计自相关函数。总体上看，密度呈现出明显的右偏形状，较短的交易持续时间频繁出现，较长的交易持续时间逐渐衰减出现，而上证B股指数样本股密度函数则更加右偏和尖峰；交易持续时间具有较强的自相关性和持续性，具有缓慢几何衰减的特点。比较而言，上证B股指数样本股交易持续时间的自相关性和持续性要强于上证50指数样本股。

表3给出了2006年8月1日至10月31日期间深市深证成份和深证B股指数各样本股的描述统计结果。从总体上看，深证成份指数样本股的平均交易持续时间明显小于深证B股指数样本股，深证成份指数样本股交易持续时间的标准差明显小于深证B股指数样本股。这说明深证成份指数样本股的交易强度和流动性明显大于深证B股指数样本股，且深证B股指数样本股的交易活动发生较为分散。就交易持续时间的分布特征而言，我们明显的观察到过度分散性(变异系数均大于1)，也就是说标准差均大于均值，这说明指数分布拟合交易持续时间的分布是不合适的。所有样本股的偏度均大于零，峰度均大于3，这说明交易持续时间的分布应该是正偏、尖峰的。比较而言，深证成份指数样本股的变异系数普遍大于深证B股指数样本股。在深证成份指数的样本股中，仅有深发展的交易持续时间的LB检验统计量的数值均远远大于5%的显著水平下的检验临界值，具有明显的自相关性，而各深证B股指数样本股的LB检验统计量的数值均远远大于5%的显著水平下的检验临界值，具有明显的自相关性。图2给出了深发展A(000001)交易持续时间的核密度估计和自相关函数。总体上看，密度呈现出明显的右偏形状，较短的交易持续时间频繁出现，较长的交易持续时间逐渐衰减，而深证成份指数样本股密度函数则更加尖峰，深证B股指数样本股密度函数则更加右偏；深证B股指数样本股的交易持续时间具有较强的自相关性和持续性，具有缓慢几何衰减的特点。比较而言，深证B股指数样本股交易持续时间的自相关性和持续性要强于深证成份指数样本股。

表2 交易持续时间的描述统计结果(2006年8月1日至10月31日，沪市)

表3 交易持续时间的描述统计结果(2006年8月1日至10月31日，深市)

比较沪、深两市样本股交易持续时间的描述统计结果，我们发现交易持续时间的分布呈现正偏、尖峰特征和过度分散性，且深圳股市的过度分散性更加明显。沪市股票交易持续时间的均值与方差均明显小于深市，这反映了沪市股票的交易强度和流动性明显大于深市，且交易活动发生较为集中。沪、深两市股票的交易持续时间经常表现出明显的自相关性和持续性，有的具有缓慢几何衰减的特点，有的则衰减较快。比较A、B两个股市，A股股票交易持续时间的均值与方差均明显小于B股股票，这反映了A股股票的交易强度和流动性明显大于B股股票，且交易活动发生较为集中。

2.3 价格持续时间的统计特征

价格持续时间是按照价格信息的变化，也就是价格绝对变化的累积对持续时间点过程进行打薄来获取的。我们常常用dp价格绝对变化的累积，为一外生变量。在本文的实证分析中，dp的数值选取为三种不同的状态以反映价格绝对变化与持续时间的关系。由于深市和沪市价格变化的最小单位为A股0.01元，B股0.001美元(沪市)或0.01港元(深市)，dp的最小取值确定为A股0.01元，B股0.001美元 (沪市)或0.01港元(深市)，其余两种状态则根据该只股票价格的波动进行确定。为了避免买卖价格跳跃导致的偏差，此处的交易价格选用中间价。

表4给出了2006年8月1日至10月31日期间样本股的描述统计结果。我们发现：（1）随着价格绝对变化累积值的dp增加，价格持续时间的平均值和标准差也增加，但是增加的趋势并非线性趋势，而是递增趋势；（2）各价格持续时间的标准差均大于平均值，表现出明显的过度分散性，价格持续时间的分布不可能是指数分布；（3）价格持续时间的LB检验统计量的数值均远远大于5%的显著水平下的检验临界值x，具有明显的自相关性，随着价格绝对变化累积值dp的增加，价格持续时间的LB检验统计量的数值逐渐递减，且递减速度逐渐减慢。

图3给出了价格持续时间的核密度估计和自相关函数。总体上看，密度呈现出明显的右偏形状，较短的交易持续时间频繁出现，较长的交易持续时间逐渐衰减，各样本股的密度函数为单峰，各样本股密度函数的右偏形状随着dp的增加拖尾现象愈加明显；各股票的价格持续时间具有不同程度的自相关性，有的具有短记忆性，有的具有长记忆性和持续性，且自相关性的特点并不随着dp的变化而发生变化。

2.4 成交量持续时间的统计特征

成交量持续时间通常定义为直到某一累积成交量被市场所吸收所需要的时间，可用来测量流动性和解释交易过程的时间与交易量之间的关系。我们常常用dv表示成交量的累积，为一外生变量。dv的数值选取为大、中、小三种不同的状态以反映成交量的累积与持续时间的关系。为简化起见，在2006年8月1日至10月31日期间，分析选用的样本股票有浦发银行(600000)、深发展 A(000001)、上电 B股(900901)、万科B(200002)。

表5给出了2006年8月1日至10月31日期间样本股的描述统计结果。我们发现：（1）随着成交量累积值dv的增加，成交量持续时间的平均值和标准差也增加，但是增加的趋势并非线性趋势，而是递增趋势；（2）各成交量持续时间的标准差均小于平均值，表现出明显的分散不足特征(变异系数小于1)，交量持续时间的分布不可能是指数分布；（3）成交量持续时间的LB检验统计量的数值均远远大于5%的显著水平下的检验临界值，具有明显的自相关性，随着成交量累积值dv的增加，成交量持续时间的LB检验统计量的数值逐渐递减，且递减速度逐渐减慢。

表4 价格持续时间的描述统计结果(2006年8月1日至10月31日)

表5 成交量持续时间的描述统计结果(2006年8月1日至10月31日)

图4给出了成交量持续时间的核密度估计和自相关函数。总体上看，密度呈现出明显的右偏形状，较短的交易持续时间频繁出现，较长的交易持续时间逐渐衰减，各样本股的密度函数为单峰，各样本股密度函数的右偏形状随着dv的增加拖尾现象愈加明显；各股票的成交量持续时间具有不同程度的自相关性，有的具有短记忆性，有的具有长记忆性和持续性，且自相关性的特点并不随着dv的变化而发生变化。

3 总结

本文首次全面基于日内交易数据考察了中国股票市场各金融持续时间的描述统计规律和分布特征，特别是将金融持续时间分为交易持续时间、价格持续时间和成交量持续时间进行深入细致的研究是本文的一个创新。

经过实证分析，得到如下有价值的结论和评述：交易持续时间存在尖峰、正偏性、过度分散性、持续自相关性，说明指数分布拟合交易持续时间的分布是不合适的；价格持续时间存在过度分散性、自相关性、记忆性和“幂律”特性。价格持续时间的记忆程度长短不一，价格持续时间的分布为右偏、单峰分布，随着的增加拖尾现象愈加明显。成交量持续时间表现出分散不足特征，其余与价格持续时间类似。

[1]Bauwens,L.,Giot,P.The Logarithmic ACD Model:An Application to the Bid-ask Quote Process of Three NYSE Stocks[J].Annales d'Economieet de Statistique,2000,60.

[2]Bauwens,L.,Veredas,D.The Stochastic Conditional Duration Model:A Latent Factor Model for the Analysis of Financial Durations[J].Journal of Econometrics,2004,119(2).

[3]Engle R.F.，Russell J.R.Autoregressive Conditional Duration:A New Model for Irregularly Spaced Transaction Data[J].Econometrica,1998,66.

[4]Engle,R.F.,Russell,J.R.Forecasting the Frequency of Changes in Quoted Foreign Exchange Prices with the Autoregressive Conditional Duration Model[J].Journal of Empirical Finance,1997,12.

[5]Engle,R.F.The Econometrics of Ultra-High Frequency Data[J].Econometrica,2000,68(1).

[6]Fernandes,M.,Grammig,J.A Family of Autoregressive Conditional Duration Models[J].Journal of Econometrics,2006,130(1).

[7]Jasiak,G.GARCH forIrregularly Spaced FinancialData:The ACD-GARCH Model[J].Studies in Nonlinear Dynamics and Economics,1998,2(4).

[8]Gouriéroux,C.,J.Jasiak,G.LeFol.Intra-day Market Activtiy[J].Journal of Financial Markets,1999,2.

[9]Manganelli,S.Duration,Volume and Volatility Impact of Trades[J].Journal of Financial Markets,2005,8.

[10]Zhang,M.Y.,Russell,J.R.,Tsay,R.S.A Nonlinear Autoregressive Conditional Duration Model with Applications to Financial Transaction Data[J].Journal of Econometrics,2001,104(1).

（责任编辑/亦 民）

O212

A

1002－6487（2010）17－0004-04

教育部人文社会科学研究资助项目（09YJC910009）；西南财经大学“211工程”三期青年教师成长资助项目（211QN09020）；西南财经大学“211工程三期”统计学重点学科建设资助项目

鲁万波（1977-），男，贵州贵阳人，博士，副教授，研究方向：非参数统计与风险管理、金融计量经济学。