正交曲线坐标系中的角动量算符

成泰民, 曹连刚, 葛崇员, 孙树生

(沈阳化工大学数理系,辽宁沈阳 110142)

正交曲线坐标系中的角动量算符

成泰民, 曹连刚, 葛崇员, 孙树生

(沈阳化工大学数理系,辽宁沈阳 110142)

由不同正交曲线坐标系的单位基矢之间的变换矩阵,推导出角动量算符之间的普遍变换规律.并且在正交曲线坐标系中给出 Hamilton算符▽及角动量算符的表示.讨论球坐标系、柱坐标系、直角坐标系之间的单位基矢之间的变换矩阵及角动量算符之间的变换规律.并讨论在球坐标系、柱坐标系、直角坐标系中^L2算符的处理.

正交曲线坐标系; 幺正算符; 角动量算符; Hamilton算符▽

在一有心力场的系统中,从有心力的力心引出的各个空间方向是等价的,所以相对于力心而言角动量是守恒的.同理,在具有轴对称性的外场中,沿该对称轴方向的角动量分量是守恒的.这些是在经典力学及量子力学中同样都成立的守恒律.但是在经典力学中 L×L=0,而在量子力学中 ^L×^L=iħ^L.这是在角动量理论部分量子力学与经典力学的最主要不同之处.球坐标系、柱坐标系中的角动量算符的表示,一般都采用球坐标系、柱坐标系中位置矢量沿基矢的分量与直角坐标系中沿 (x,y,z)轴方向的分量关系处理的[1-4].这种处理较繁琐,并且 Ham ilton算符▽、拉普拉斯算符▽2在球坐标、柱坐标中的表示在物理学中经常用到.因为球坐标、柱坐标、直角坐标都属于正交曲线坐标系,因此,在正交曲线坐标系中表示上述算符及探讨不同正交曲线坐标系之间的变换规律,找出普遍规律,具有重要的意义.

1 角动量算符在不同正交曲线坐标系中

的变换规律[5-6]

正交曲线坐标系 (u,v,w)中的单位基矢的表示及正交关系如下:

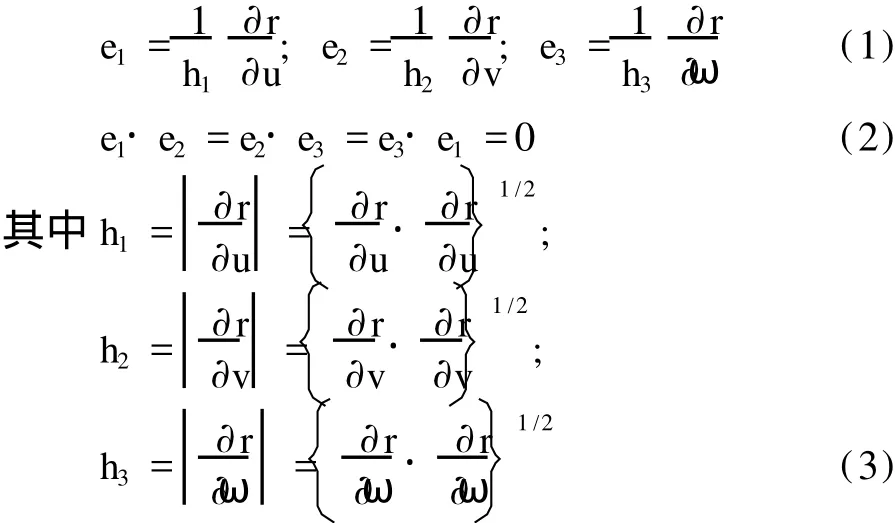
正交曲线坐标系 (u,v,ω)中的 Ham ilton算符▽的表示为:

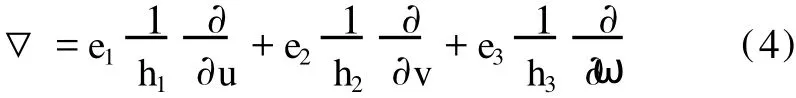
角动量算符在正交曲线坐标系 (u,v,ω)中表示为 ^L=^r×^p.因在坐标空间中 ^r是自表示,所以 ^r=r=r1e1+r2e2+r3e3,并且动量算符在坐标空间中表示为 ^p=-iħ▽.

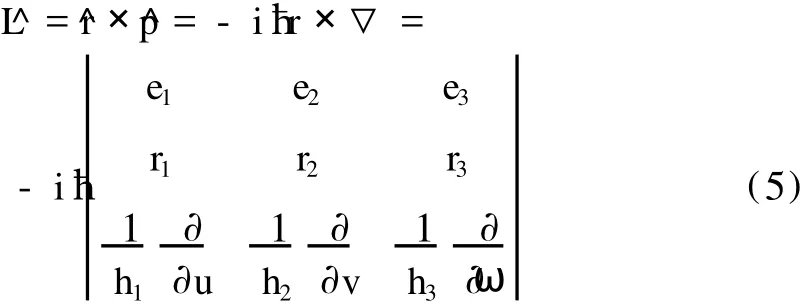
由(5)式可知,角动量算符在正交曲线坐标系 (u,v,ω)中矩阵形式表示如下:

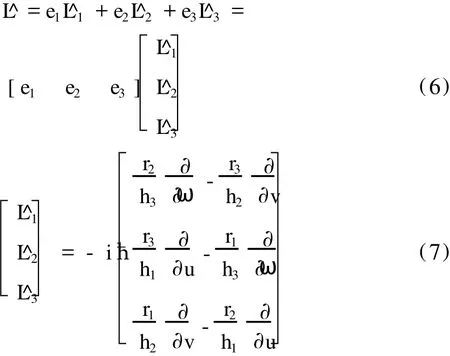
同理在另一正交曲线坐标系 (u′,v′,ω′)中矩阵形式表示如下:

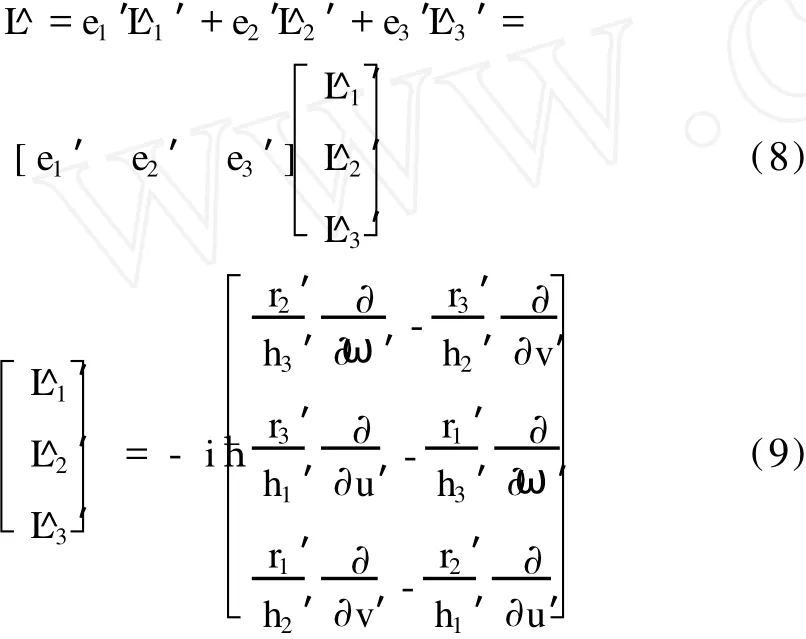
其中 ^r=r=r1′e1′+r2′e2′+r3′e3′,e1′、e2′、e3′是另一正交曲线坐标系 (u′,v′,ω′)的单位基矢,其表示如下:

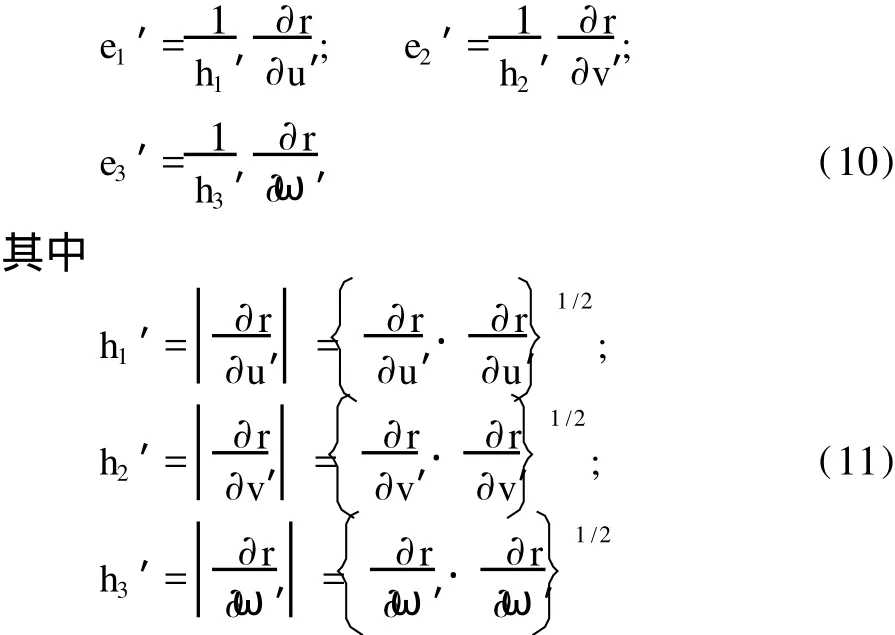
为了得到角动量算符的表示在不同的正交曲线坐标系之间的变换规律,首先须知道不同的正交曲线坐标系的单位基矢之间的变换规律.由(3)式与 (11)式可得:

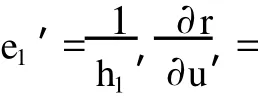
所以不同正交曲线坐标系的角动量算符之间的变换规律如下:

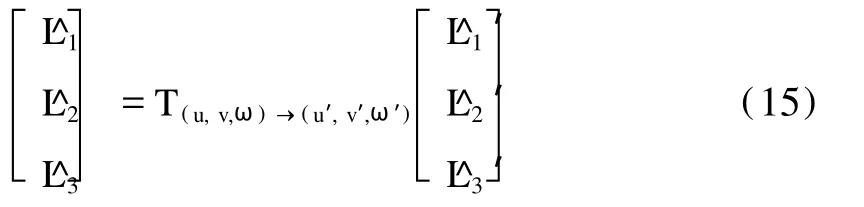
2 讨 论

2.1 角动量算符在球坐标系与直角坐标系之间的变换关系[7]

令 (u,v,ω)↔(x,y,z),(u′,v′,ω′)↔(r,θ,φ),并且由 (3)式、(11)式,可求得如下结果:

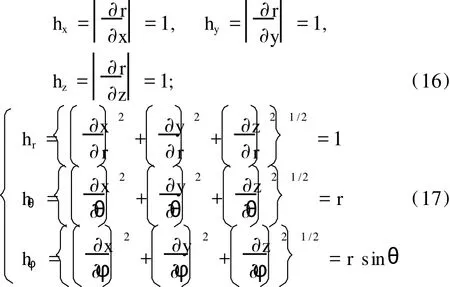
在 (17)式的推导中,利用了 x=r sinθcosφ、y= r sinθsinφ、z=r cosθ关系.

由 (9)式与 r=rer(即 r1′=r,r2′=r3′=0),可得球坐标下的角动量算符矩阵表示如下:

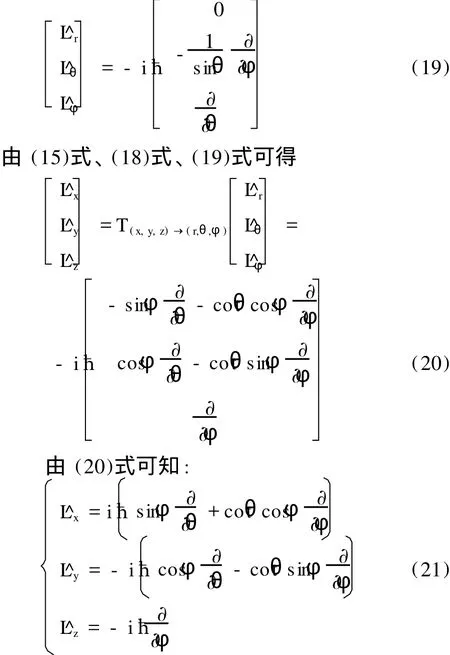
(22)式这一关系只在直角坐标系上成立,在球坐标系 (即=≠++)和柱坐标系 (即=^L·^L≠)中不成立.这是因为直角坐标系的单位基矢是常矢量,但是对随位置矢量的变化,单位基矢发生变化的正交曲线坐标系而言,必须考虑单位基矢相对于坐标的变化率不为零条件[8](即如/∂φ=-sinθer-).

球坐标系的单位基矢的偏导数如下:

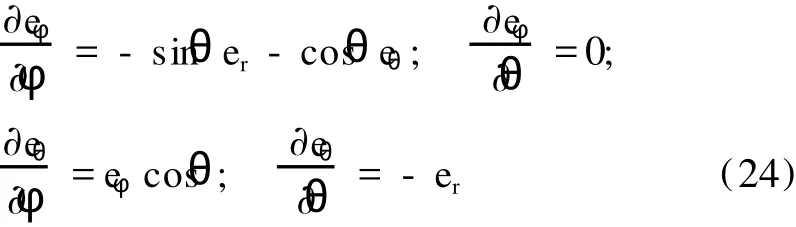
由 (19)式得:

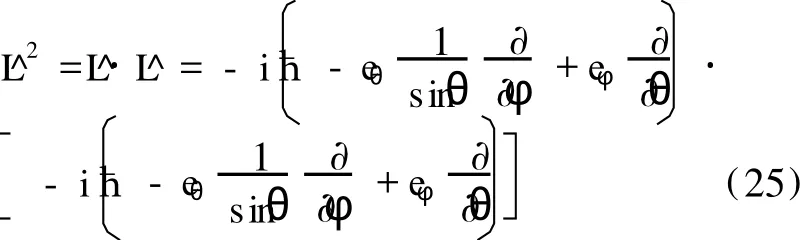
根据 (24)式、(25)式和球坐标系的单位基矢之间的正交性 er·eθ=eθ·eφ=eφ·er=0,也可以得到(23)式的结果.

2.2 角动量算符在柱坐标系与直角坐标系之间的变换关系

令 (u,v,ω)↔(x,y,z),(u′,v′,ω′)↔(ρ,φ, z),并且由 (11)式,可求得如下结果:

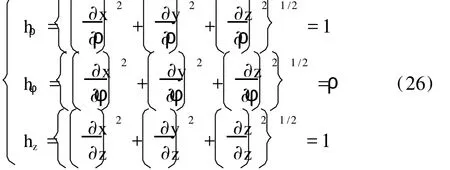
在(26)式的推导中,利用了 x=ρcosφ、y= ρsinφ、z=z关系.

由(14)式、(16)式、(26)式,可得柱坐标系与直角坐标系的单位基矢之间的变换矩阵如下:

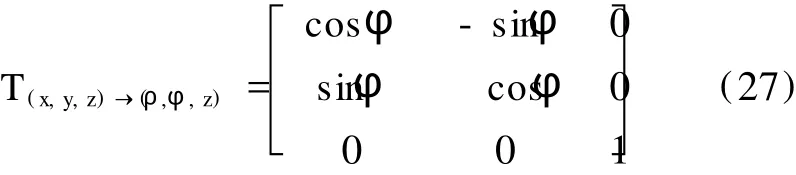
由 (9)式与 r=ρeρ+zez(即 r1′=ρ,r2′=0, r3′=z),可得柱坐标下的角动量算符的矩阵表示如下:

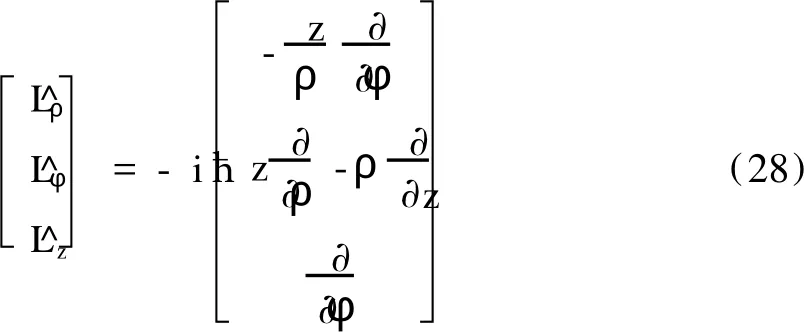
由 (15)式、(27)式、(28)式可得:

在柱坐标系利用 (22)式计算 ^L2,比利用柱坐标系的单位基矢偏导数方法繁琐.

柱坐标系的单位基矢的偏导数如下:

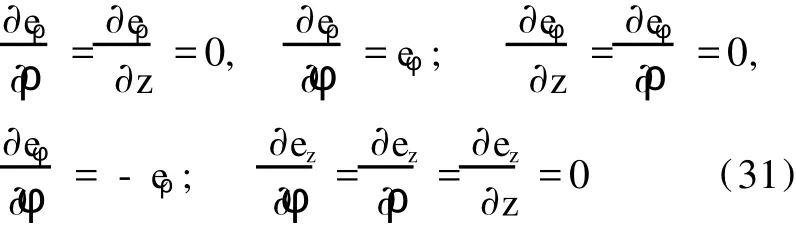
由(31)式和柱坐标系的单位基矢之间的正交性 eρ·eφ=eφ·ez=ez·eρ=0,按后一种方法计算如下:

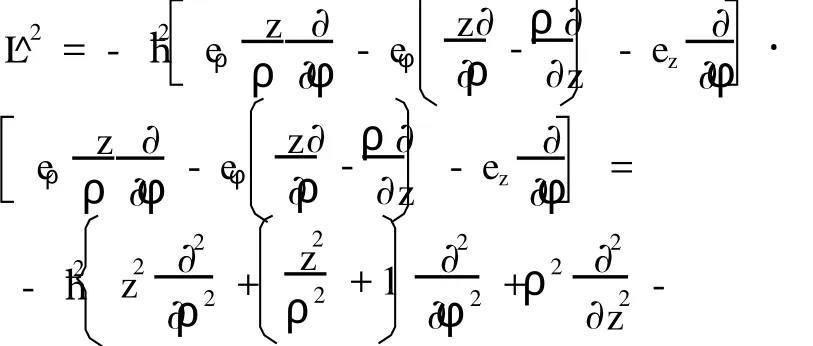
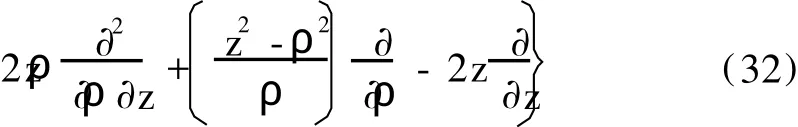
2.3 角动量算符在球坐标系与柱坐标系之间的变换关系

由普遍方法也可以处理,但已知 2.1、2.2前提下,利用不同的正交曲线坐标系的单位基矢之间变换矩阵 T(u,v,ω)→(u′,v′,ω′)的幺正性,能够容易得到下列结果.

由 (13)式得

根据 (33c)式、(36)式、(18)式、(35b)式可得:

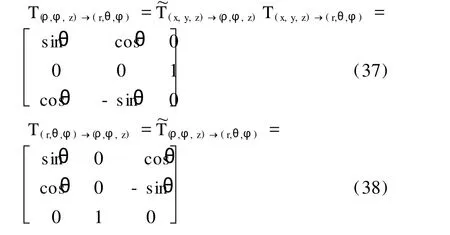
由 (15)式得:

[1] 林辛未,殷传宗.量子力学中的角动量[M].重庆:西南师范大学出版社,2008:49-54.

[2] 尹鸿钧.量子力学[M].合肥:中国科技大学出版社,1999:106-108.

[3] 周世勋.量子力学教程[M].北京:高等教育出版社,2003:60-63.

[4] 曾谨言.量子力学 (卷Ⅰ)[M].北京:科学出版社,1990:167-169.

[5] 郭硕鸿.电动力学[M].2版.北京:高等教育出版社,1997:340-346.

[6] 四川大学数学系高等数学教研室.高等数学 (物理类专业用,第二册)[M].2版.北京:高等教育出版社,1991:251-257.

[7] 钱伯初.量子力学 [M].北京:高等教育出版社, 2006:332-333.

[8] 成泰民,孙树生.正交曲线坐标系中的单位基矢的导数[J].大学物理,2010,29(6):27-29.

AngularMomentum Operators in O rthogonal Curvilinear Coordinate System s

CHENG Tai-m in, CAO L ian-gang, GE Chong-yuan, SUN Shu-sheng
(Shenyang University of Chem ical Technology,Shenyang 110142,China)

Using the transform ation m atrix be tween the unit basis vectors in deferent or thogonal curvilinear coordinate system s,we deduce the general form of the transform ation be tween the angularm om entum operators in these coordinate system s.We give the representations of Ham ilton operator▽ and angular mom entum operators in the orthogonal curvilinear coordinate system.We discuss the transform ation m atrix of unit basis vectors am ong the spherical coordinate system,cylindrical coordinates system and rectangular coordinates system,and the transform ation betw een the angularm om entum operators.Furtherm ore,we discuss the treatm ent of L2operator in different coordinate systems.

orthogonal curvilinear coordinates system; unitary operator; angularm om entum operators; Ham ilton operator▽

O413.1

A

1004-4639(2010)04-0365-05

2010-07-12

国家自然科学基金资助项目(10647138);辽宁省教育厅科学研究资助项目(20060667)

成泰民(1970-),男,辽宁沈阳人,副教授,博士,主要从事理论物理学教学及磁性物理研究工作.