基于差分神经网络的热处理炉钢板温度预报研究

李 静,王 京,赵云涛

(北京科技大学冶金工程研究院,北京,100083)

基于差分神经网络的热处理炉钢板温度预报研究

李 静,王 京,赵云涛

(北京科技大学冶金工程研究院,北京,100083)

针对热处理炉钢板温度模型建立困难、准确性差等问题,采用差分进化算法与神经网络相结合的方法,建立了基于差分神经网络的热处理炉钢板温度预报模型。结果显示了该钢板温度预报模型具有较高的精度。关键词:差分进化算法;神经网络;热处理炉;钢板温度预报

热处理炉钢板的热交换是一个非常复杂的过程,伴随着相变潜热的释放,其表面受到炉内火焰、炉墙、炉气热辐射以及炉内气体对流的影响,其炉内温度分布无法依赖现有的技术手段进行检测,更难以用精确的数学模型描述。以往的研究大多是从钢板在炉内的热传导偏微分方程入手,通过求解偏微分方程,得到钢板在加热过程中的温度分布。上述研究方法有两个缺点:一是由于对钢板加热过程需要做过多的假设,使得预报模型的温度精度大打折扣;二是由于钢板加热过程具有典型的分布参数特性及复杂的边界条件,使得偏微分方程的求解复杂。而神经网络具有自学习、自组织、自适应和非线性动态处理等特性,因而可用于热处理炉钢板的温度预报。但是BP神经网络在使用过程中存在易陷入局部最优等缺陷。

本文利用差分进化算法对神经网络结构参数和权值阈值自动寻优,通过大量学习样本训练验证,使差分神经网络较BP网络在温度预报精度方面有明显提高。

1 差分进化算法数学模型

差分进化算法(DE)求解优化问题时,通过N P个个体在搜索空间内共同完成并行搜索。DE的基本操作包括变异、交叉和选择3种操作。初始种群是在搜索空间内随机生成的,一般采用均匀分布的随机函数来产生。然后随机选择两个不同的个体矢量相减生成差分矢量,再将差分矢量赋予权值后加到第三个随机选择的个体矢量上,生成变异个体,该操作称为变异。变异个体与目标个体进行参数混合,生成试验矢量,这一过程称为交叉。如果试验矢量的适应度优于目标个体的适应度,则用试验矢量取代目标个体而形成下一代新个体,该操作称为选择[1]。

设N P个维数为D的实数向量作为每代种群,每个个体可表示为[2]

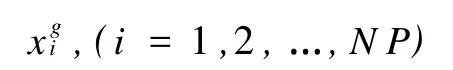
式中:i为个体在种群中的序列;g=1,2,…,G为进化代数;N P为种群规模,进化过程中,N P始终保持不变[3]。

1.1 初始化

为建立优化搜索的初始点,种群首先需要被初始化。通常生成初始种群的一个方法是从给定边界约束内的值中随机选择,在DE研究中,一般假定所有随机初始化种群均符合均匀概率分布。

设参数变量界限为 x(L)ij≤xij≤x(U)ij,则

式中:rand[0,1]为[0,1]之间产生的均匀随机数。

1.2 变异操作

对于每个目标个体 xgi(i=1,2,…,N P),基本DE算法的变异个体产生如下:

式中:随机选择的序号 r1、r2、r3互不相同,且 r1、r2、r3与目标个体序号 i也不同,所以须满足 N P≥4。变异算子 F∈[0,2]是一个实常数因数,控制差分矢量的放大作用。

1.3 交叉操作

为了增加种群的多样性,引入了交叉操作,对变异操作获得的变异个体 vig和对应的目标个体xig按式(3)进行交叉生成试验矢量 uig

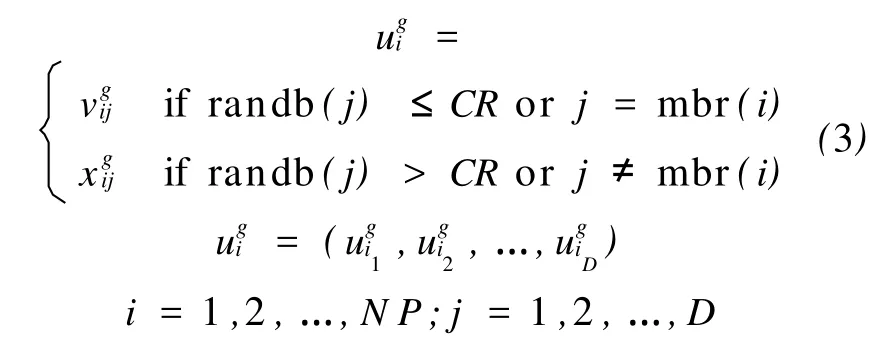
1.4 选择操作

为保证选择较优的个体进入下一代,DE按照贪婪准则将试验矢量 ugi与当前种群中的目标个体xgi进行比较。如果目标函数最小化,那么具有较小目标函数值的矢量将在下一代种群中赢得一席之地,即

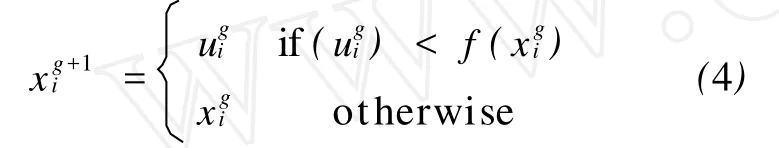
1.5 边界处理

在有边界约束的问题中,确保产生的新个体位于问题可行域中是必要的,一个简单方法是将不符合边界约束的新个体用可行域中随机产生的参数向量代替。即:

2 差分进化算法优化神经网络步骤

神经网络可以实现非线性映射过程,并且具有大规模计算的能力,在实际中得到了大量应用。用BP神经网络解决问题的过程就是设计适当的网络结构和构造相应的网络权值阈值的过程。目前设计BP网络方法主要是探测训练法。权值是通过不断前向计算和反向误差传播得到的,而结构的获取采用逐步递减(增)的方式进行实验探测,这既不能避免反向传播算法所固有的不足,也使训练出的网络性能过分依赖于具体的探测过程。为了设计出性能优良适合于具体应用的神经网络模型,设计过程中应将网络拓扑结构的动态调整和权值阈值训练的动态特性协调起来,从而全局性地优化神经网络性能。因此将差分进化算法和神经网络相结合,利用差分进化算法优于遗传算法的全局搜索能力特点,对神经网络的网络结构、各层神经元的连接权、阈值进行最优化设计,模型结构形式如图1所示。

图1 差分算法优化神经网络模型结构Fig.1 Basic principlesof optim ized neural networks by differential evolution algorithm

将差分进化算法用于优化神经网络的结构及权值阈值,首先需列出神经网络中所有可能存在的神经元,并将这些神经元的连接权值阈值及结构参数编码成实数码串表示的个体。然后随机生成这些码串群体,进行差分进化算法优化计算,利用差分进化算法的全局优化及隐含并行性的特点提高权值及参数的优化速度。最后将较优码串个体解码成神经网络结构及权值阈值参数,将所有预测样本通过此神经网络就可得到较优的学习预报值。具体步骤如下:

Step 1.随机产生若干个参数不同的神经网络,对每个网络编码表示,其中每个网络对应一个个体,n个个体构成一个种群;

Step 2.将每个个体编码成不同的神经网络,分别对每个网络进行测试;

Step 3.计算每个个体对应神经网络的误差函数,确定每个个体的适应度;

Step 4.判断是否达到最大进化代数或达到精度要求,是则转Step 6,否则继续;

Step 5.利用变异、交叉、选择等差分操作算子对当前群体进行处理,产生新一代群体,转Step 2;

Step 6.将种群中适应度最高的个体解码成神经网络结构及权值阈值参数;

Step 7.结束。

3 差分神经网络温度预报结构设计

3.1 输入层、输出层的设计

通过对热处理炉内钢板加热过程的研究,总结出以下一些影响钢板温度的主要因素:

(1)钢种是影响钢板温度升温快慢的主要因素,它也会影响到钢板的其他参数,如钢板的密度、导热系数、线膨胀系数等。但是对于同种钢板,其钢种是一样的,就是说在升温过程中,这些参数只和钢板的温度有关,即和钢板上时刻的温度(上时刻温度测量采用目前研究加热炉热交换最有效的“黑匣子”方法,即在实验钢板内埋入热电偶)有关系。所以,钢种不作为粒子群神经网络的输入量。

(2)炉膛温度是影响钢板温度加热快慢的重要因素,不同的炉膛温度具有不同的边界物流qu和qs。

(3)钢板尺寸也会很大程度地影响到钢板的温度,其中,钢板厚度是影响钢板温度的主要因素。这里把钢板的长、宽、高都做为影响粒子群神经网络的输入量。

(4)辊道速度。对于不同尺寸和不同钢种的钢板,可能会采取不同的热处理制度,所以会有不同的热处理速度,因此把辊道速度也作为粒子群神经网络的输入量。

总之,把钢板的长度、宽度、厚度、辊道速度、钢板所处上部、下部炉膛的温度、钢板上时刻的温度这7个量作为神经网络的输入,钢板在本时刻的温度作为神经网络的输出,即输出层只有一个神经元。

3.2 网络训练精度设计

提高网络训练的精度,既可以通过增加隐层数来实现,也可以通过增加隐层的节点数来实现[4]。本文将隐层数固定为一层,而只对单隐层的节点数进行自动寻优。隐层和输出层节点激活函数均采用Sigmoid函数。

3.3 差分神经网络参数设置

利用差分进化算法对神经网络进行结构和权值阈值优化的码串由五部分组成:各隐层节点数、输入层到隐层连接权值、隐层到输出层连接权值、隐层阈值、输出层阈值。设该单隐层网络的输入层单元数、隐层单元数和输出层单元数分别为m、p和q。

码串总长度 H包括了网络结构、连接权值和阈值的所有信息。码串结构如图2所示:

图2 差分神经网络码串结构图Fig.2 Code string chart of differential neural network

以训练集样本对作为差分神经网络的输入和期望输出,计算出网络输出和期望输出的误差,取误差平方和作为适应度函数 J[6]。

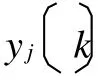
差分进化算法其他参数设置为:种群大小60;CR=0.8;F=0.5。

4 仿真

通过matlab编程语言,利用热处理炉生产过程中的历史数据,对预报钢板温度的差分神经网络进行离线学习和测试。本文取厚度分别为55、45、60、70的600组数据作为差分神经网络的训练数据,取同一块钢板的70组数据作为测试数据。分别用BP神经网络和差分神经网络在相同精度(0.002)要求下对辊底式热处理炉钢板表面平均温度和钢板芯部温度进行了训练。

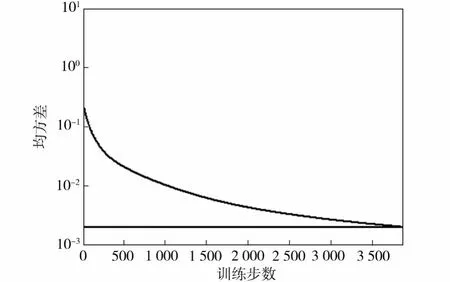
图3 BP网络钢板表面温度误差曲线Fig.3 Steel plate surface tem perature error curve of BP network

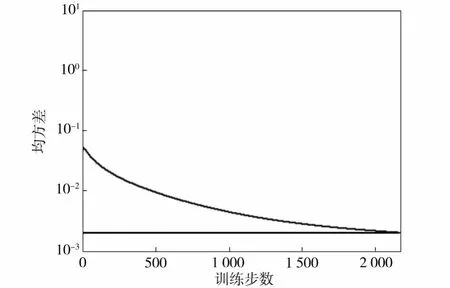
图4 差分神经网络钢板表面温度误差曲线Fig.4 Steel plate surface temperature error curves of differential neural network

图3为BP神经网络训练结果;图4为差分神经网络训练结果。由图3、图4可知,直接训练BP神经网络需要3 863次达到精度要求,而神经网络达到相同精度要求只需要训练2 174次,显然比直接训练BP神经网络快了43.7%,速度显著提高。用差分神经网络建立的辊底式热处理炉钢板表面温度预报曲线如图5所示。由图5可以看出,用差分神经网络建立的钢板表面平均温度在炉内3段均满足误差要求。

图5 钢板表面平均温度预报曲线Fig.5 Average tem perature prediction curve of steel plate surface

图6 BP网络钢板芯部温度误差曲线Fig.6 Steel center temperature error curves of BP network

图6为BP神经网络训练结果;图7为差分神经网络训练结果。由图6、图7可知,直接训练BP神经网络需要4 625次达到精度要求,而差分神经网络达到相同精度要求只需要训练3 563次,显然比直接训练BP神经网络快了22.9%,速度显著提高。用差分神经网络建立的辊底式热处理炉钢板芯部温度预报曲线如图8所示。由图8可以看出,用差分神经网络建立的钢板芯部温度在炉内3段均满足误差要求。

图7 差分神经网络钢板芯部温度误差曲线Fig.7 Steel center temperature error curves of differential neural network

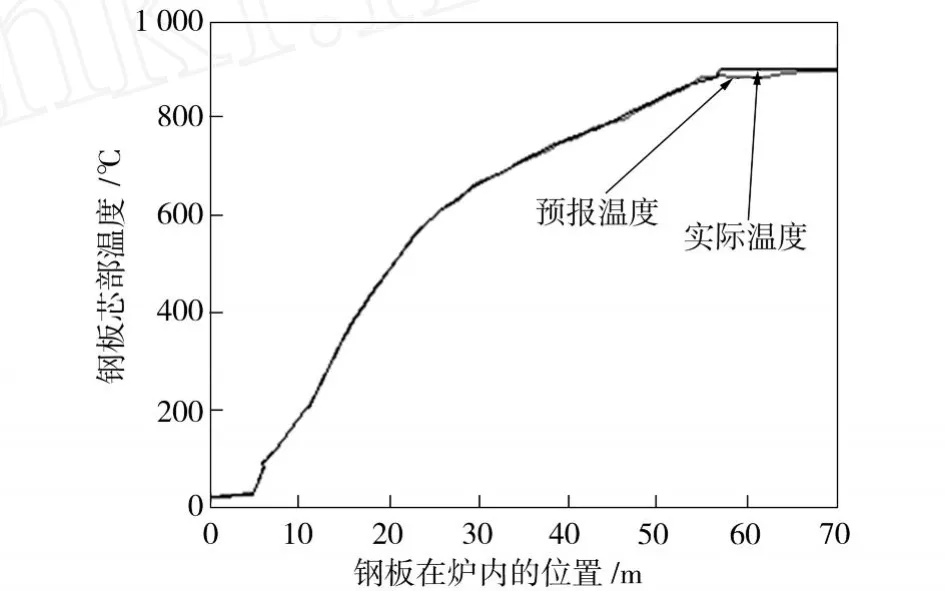
图8 差分神经网络温度预报曲线Fig.8 Temperature prediction curve of differential neural network

5 结语

基于差分进化算法的优化神经网络算法具有快速寻优能力;差分进化算法优化神经网络的温度预报模型能用于辊底式热处理炉钢板表面平均温度和中心点温度的预报,且具有较高的预报精度。

[1] Storn R,Price K.Differential evolution-a simp le and efficient adap tive scheme for global op timization over continuous spaces[R].Berkeley:International Computer Science Institute,1995.

[2] 汪琍,张铃.用网格实现交叉操作的遗传算法[J].计算机工程与科学,2000,22(1):18-20.

[3] Storn R.On the usage of differential evolution forfunction optimization[C]∥Proceedings-the Biennial Conference of the North American Fuzzy Information Processing Society.Piscataway,NJ,USA: IEEE,1996:519-523.

[4] 符强,张进之.基于人工神经网络的热连轧参数预测模型[J].钢铁研究学报,2003,15(4):70-72.

[5] 邱红雷,田勇,赵忠.结合模型自适应的神经元网络在中厚板轧机轧制力预报中的运用[J].钢铁研究学报,2006,18(6):59-62.

[6] Fechner T,Neumerkel D,Keller I.Adaptive neural network filter for steel rolling[J].IEEE World Congress on Computational Intelligence,1994,6 (27):3 915-3 920.

Steel tem perature prediction of heat treatmen t furnace based on differential neural network algorithm

L i Jing,W ang Jing,Zhao Yuntao
(Engineering Research Institute of University of Science and Technology Beijing,Beijing 100083,China)

The steel temperature model of heat treatment furnace is difficult to establish and has poo r accuracy.Differential evolution algorithm and neural network were combined to app roach the p roblem.Firstly,neural network structure and weightsof thresholdswere op timized by differential evolution algorithm w hich exhibited fair performance for convergence speed,thus the differential neural netwo rk w as constructed.Then,through analyzing the impact facto rs of steel temperature,the p late temperature p rediction model based on differential neural network was established.The results show that the steel temperature p rediction model imp roves forecast accuracy.

differential evolution algo rithm;neural network;heat treatment furnace;steel temperature p rediction

TP301

A

1674-3644(2010)05-0492-05

[责任编辑 彭金旺]

2010-04-12

“十一五”国家科技支撑计划项目(2006BAE03A 06).

李 静(1973-),女,北京科技大学副研究员,博士.E-mail:lijing@nercar.ustb.edu.cn

王 京(1948-),男,北京科技大学教授,博士生导师.E-mail:wangj@nercar.ustb.edu.cn