82B高碳钢热变形行为研究

张云祥,余弛斌,杭乃勤,赵嘉蓉

(武汉科技大学材料与冶金学院,湖北武汉,430081)

82B高碳钢热变形行为研究

张云祥,余弛斌,杭乃勤,赵嘉蓉

(武汉科技大学材料与冶金学院,湖北武汉,430081)

采用单道次热压缩实验方法,在Thermomaster-Z型热模拟试验机上模拟高碳钢高速线材热轧变形过程动态再结晶行为,测定82B高碳钢在变形温度为800～1 100℃、变形速率为0.1～50 s-1、变形程度为0～0.60条件下的真应力-应变曲线,利用曲线特征值确定高应变速率下的变形激活能,根据实验结果分析动态再结晶变形条件,建立动态再结晶状态图。

高碳钢;变形激活能;动态再结晶

动态再结晶作为钢材生产过程中的一个重要冶金物理现象,对于高碳高速线材钢的组织性能控制有重要影响[1]。关于低碳钢及其在低变形速率下的动态再结晶行为的研究较多[2-3],有关高碳钢及其在高应变速率下的热变形行为的研究鲜见报道。本文采用单道次热模拟实验方法,在Sellars组织演变模型的基础上,研究82B高碳钢热变形激活能及其动态再结晶变形条件,研究高碳钢在高变形速率下的热变形行为。

1 实验材料及方案

试样取自某高速线材车间SWRH82B高碳钢坯,其化学成分(wB)为:0.82%C,0.21%Si, 0.74%M n,0.016%P,0.003%S,0.016%Cu, 0.174%Cr,0.018%Ni;试样为中空管状,外径8 mm,内径6.4 mm,高12 mm。

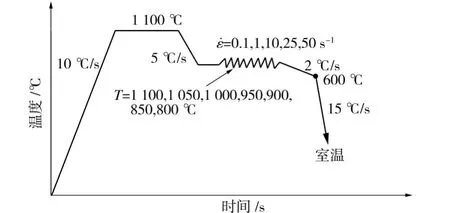
图1 单道次圆柱体压缩热模拟实验工艺Fig.1 Diagram of single pass cylindrical compression experiment

对 35个试样在 Thermomaster-Z热模拟机上进行单道次压缩试验,实验工艺如图1所示。所有试样均以10℃/s的速度加热到1 100℃,保温360 s;再以5℃/s的冷却速度分别冷却至800、850、900、950、1 000、1 050、1 100℃;分别以0.1、1、10、25、50 s-1的变形速率进行变形实验;变形后立即以2℃/s的速度冷却至600℃,再以15℃/s的速度快冷至室温。

2 实验结果

实验所得试样真应力-真应变曲线如图2所示。由图2可以看出,温度为800～1 100℃时,在上述变形速率范围内试样均发生了明显的动态再结晶过程。变形温度 T和应变速率ε·等对奥氏体高温变形行为都有明显的影响。在给定的变形温度和应变速率范围内,动态再结晶易发生于较高变形温度和较低应变速率条件下,并且随变形温度的降低和应变速率的增大,峰值应力σP和峰值应变εP增大,发生再结晶的临界应变值增大。

从图2中还可以看出,高温奥氏体的形变,通过加工硬化和动态软化两种机制同时起作用。在变形初期,加工硬化趋势明显,随着变形量增大,位错密度不断增大,使得变形应力不断增大。同时,由于高温条件下的变形,使得位错容易通过滑移和攀移方式产生动态回复,使加工硬化作用减弱,应力-应变曲线斜率减小;由于变形量的继续增大,位错密度不断增大,内部储存能也继续增大,当变形量达到动态再结晶临界变形程度时,将发生动态再结晶;随着变形的继续进行,金属内部不断发生动态再结晶,在应力-应变曲线上的表现是随应变增加,应力不断减小。温度为800～950℃、变形速率为0.1 s-1时,峰值应变(峰值应力所对应的真应变)为0.1～0.3;变形速率为1 s-1时,峰值应变为0.2～0.3;变形速率为10、25 s-1时,峰值应变为0.3～0.4;变形速率为50 s-1时,峰值应变为0.4～0.5。

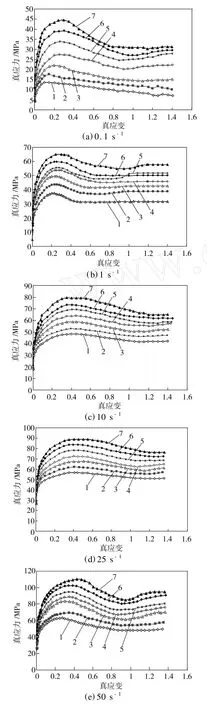
图2 试样真应力-真应变曲线Fig.2 Stress-strain curves obtained at differnet strain rates

实际生产中的变形速率一般都会超过 10 s-1,发生动态再结晶的临界应变约为0.3～0.4,因此为了使轧件发生动态再结晶,应尽量加大前面道次的压下率,以利于奥氏体晶粒的细化。

3 确定变形激活能和建立 Zener-Hollomon方程

由于热变形是一个热激活的过程,因此温度和变形速率对变形的影响可以通过引入 Zener-Hollomon参数进行研究,而 Z参数是峰值应力的函数,即:

式中:Q为变形激活能,kJ/mol;R为气体常数,R =8.314 J/(mol·K);T为绝对温度,K;σP为峰值应力,M Pa。

3.1 峰值应力、峰值应变计算

通过应力-应变数据整理出峰值应力、应变值数据,并作出峰值应力σp同温度、应变速率的关系曲线如图3、图4所示。

图3 温度对试样峰值应力的影响Fig.3 Effect of temperature on the sample’s peak stress

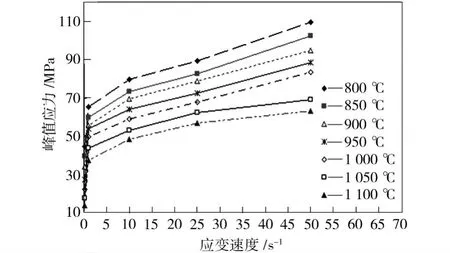
图4 应变速率对试样峰值应力的影响Fig.4 Effect of strain rate on the sample’s peak stress

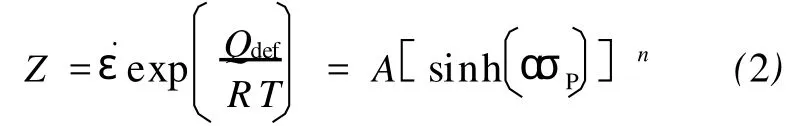
式中:n为模型系数;A,α为与钢种有关的参数,A取值0.2,α取值0.012[5]。

由式(2)可得:

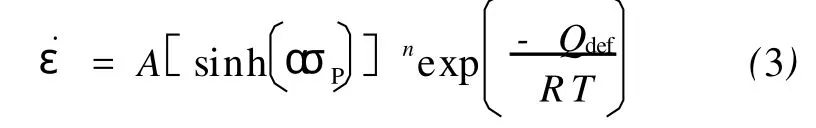
对式(3)两边取对数,有:

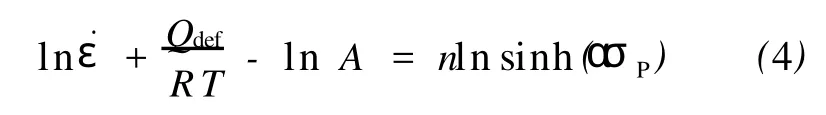
3.2 温度相关系数b值计算

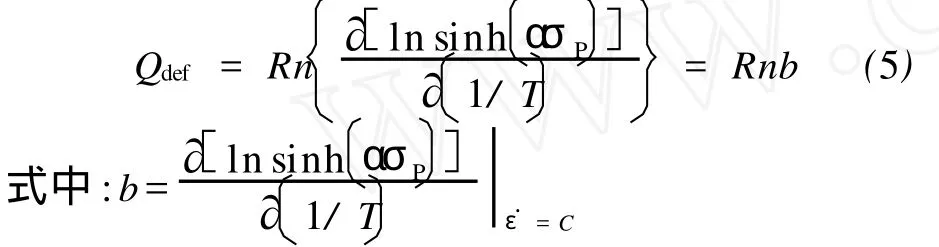
b为Zener-Hollomon参数与温度T的线性相关度,表征轧制温度对 Z参数的影响程度。根据峰值应力对应的数据,作出变形速率分别为0.1、1、10、25、50 s-1时ln sinh(ασP)同 1 000/ (T+273)的关系曲线如图5所示。由图5得到各直线平均斜率为 b=3.491 4。不同变形速率下的平均斜率b值相当于消除了变形速率的影响。

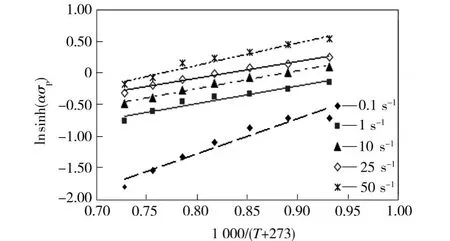
图5 不同变形速率下的b值Fig.5 b value at different strain rates

3.3 变形速率相关系数n值计算

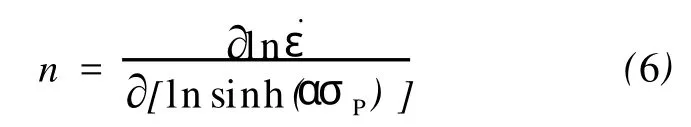
n为描述真应力-应变曲线的硬化指数,本文计算n值时,采用固定变形温度值对式(4)中求偏导数,所以n称之为变形速率相关系数。ln sinh(ασP)与之间存在线性关系,对数据进行线性回归,其关系曲线的斜率平均值的倒数即为n。由此绘制lnsinh(ασP)与ln不同温度下的数据点和拟合直线如图6所示,得到直线斜率平均值的倒数为 n=5.079 8。

图6 ln sinh(ασP)与在不同温度下的数据点和拟合直线Fig.6 n value at differen t tem peratures

3.4 变形激活能Q值计算

将b和n值代入式(5),得到热变形激活能为

Qdef=Rnb=147.408 kJ/mol

本文计算的变形激活能与文献[6]报道的数据基本一致,本文计算结果与其他文献报道结果对比如表1所示。

表1 本文结果与文献报道结果对比(Qdef/kJ·mol-1)Table 1 Value of deformation activation energy

3.5 Zener-Hollomon方程

将Qdef值代入Zener-Hollomon参数方程(1)中,得:

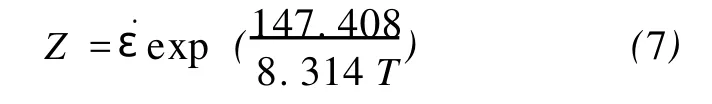
4 动态再结晶体状态图

变形特征值,即峰值应变εP和稳态应变εS可在应力-应变曲线上峰值应力处和应力下降后第一个拐点处(或应力降到稳态处)得到。动态再结晶临界应变值εC可根据εC=(0.6～0.85)εP算得,此处取εC=0.8εP。根据式(7)计算出不同条件下的 Z值如表2所示。

由εC和εS可绘制出动态再结晶图。根据表2分别作变形速率为1、25 s-1时的动态再结晶图 ,如图7所示,图7中A、B、C三个区域分别表示未动态再结晶、部分动态再结晶和完全动态再结晶。由图7中可以看出,动态再结晶临界应变在0.2～0.4之间,稳态应变在0.8～1.2之间,随着变形温度的提高,发生和完成动态再结晶所需要的临界变形量逐渐减小。根据动态再结晶变形特征值表2可以看出:当 Z值较小时(变形温度高、变形速率小),临界应变小;当 Z值较大时(变形温度低、变形速率大),临界应变大。

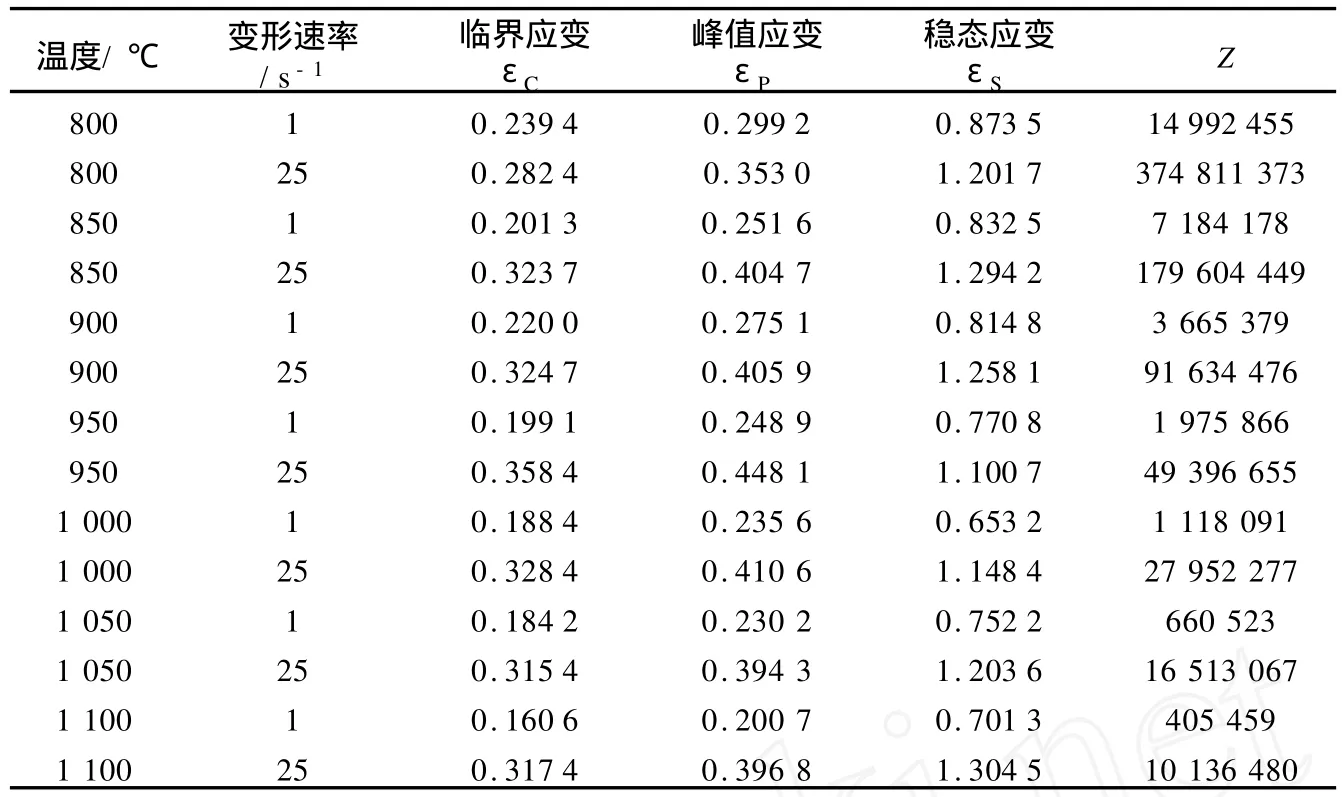
表2 变形特征值Table 2 Deformation characteristic values

图7 动态再结晶区域图Fig.7 Recrystallizatioin regionalmap

由于完成再结晶过程的真应变为0.8～1.2,即相当于绝对压下率为60%～80%,表明在进行高碳钢轧制时,应尽量增大前面高温机架压下量,后面机架绝对压下率应小于25%,方可避免发生动态再结晶。

5 结语

(1)采用单道次热模拟实验方法,得到不同工艺条件下的应力应变曲线,分析了82B高碳钢的热变形行为,利用曲线特征点确定高应变速率下82B钢的变形激活能(Qdef=14.740 8 kJ/mol),得出 Zener-Hollomon参数方程为 Z=exp

(2)82B高碳钢发生动态再结晶的临界真应变为0.2～0.4,动态再结晶稳态真应变值为0.8～1.2,根据实验结果可建立动态再结晶状态图。

[1] 赵嘉蓉,杭乃勤,张云祥.高碳钢线材组织与性能预报模拟软件的开发[J].武汉科技大学学报:自然科学版,2006,29(2):112-114.

[2] 窦晓峰,鹿守理,赵辉.Q235钢动态再结晶模型的建立[J].北京科技大学学报,1998,20(5):20-24.

[3] 魏洁,唐广波,刘正东.碳锰钢热变形行为及动态再结晶模型[J].钢铁研究学报,2008,20(3):31-35.

[4] Zener C,Hollomon J.Effect of strain rate upon p lastic flow of steel[J].Journal of App lied Physics, 1944,15(1):22-32.

[5] 余驰斌,叶传龙,赵刚,等.Nb-Ti钢高温变形时动态再结晶行为及模型探讨[J].武汉科技大学学报:自然科学版,2003,26(4):334-336.

[6] Anell E.Application of mathematical modeling to hot rolling and controlled cooling of w ire rods and bars[J].ISIJ International,1992,32(3):440-449.

[7] Devadas C,Samarm sekera I V,Haw bolt E B.The thermal and metallurgical state of steel strip hot rolling:part I[J].Characterization of Heat Trans-fer,Metallurgical Transacton A,1991,22A:307-318.

[8] Sellars C M.Modelling microstructural development during hot rolling[J].Journal of Materials Science and Technology,1990,15:1 072-1 081.

[9] Hodgson P D,Gibbs R K.A mathematical model to p redict themechanical p roperties of hot rolled CM n and microalloyed steels[J].ISIJ International, 1992,32(12):1 329-1 338.

Hot deformation behavior of high carbon steel 82B

Zhang Yunxiang,Yu Chibin,H ang N aiqin,Zhao Jiarong
(College of Materials Science and Metallurgy,Wuhan University of Science and Technology,Wuhan 430081,China)

Single comp ression deformation tests were conducted on Thermomaster-Z thermal simulator and dynamic recrystallization behavior of high carbon steel in high speed rolling was investigated.The true stress strain-curves w ere measured under the conditions of defo rmation temperature of 80 0～1 100℃,defo rmation rate of 0.1～50 s-1and strain of 0～0.60.By meansof the curve’s characteristic value and linear regression,the hot deformation activation energy in the condition of high strain rate for high carbon steel 82B was determined and it equaled 147 kJ/mol.The critical value of dynamic recrystallization occurred is analyzed and the dynamic recrystallization diagram is given.

high carbon steel;deformation activation energy;dynamic recrystallization

TG142.1+1

A

1674-3644(2010)05-0473-05

[责任编辑 彭金旺]

2010-06-07

张云祥(1970-),男,武汉科技大学副教授,博士.E-mail:zhangyunxiangwust@163.com

作者介绍:张云祥,男,1970年出生,1994年西安建筑科技大学金属压力加工系毕业,2000年获武汉科技大学材料加工工程硕士学位,2010年获华中科技大学材料加工工程博士学位。现为武汉科技大学材料与冶金学院副教授。主要从事材料成型计算机控制、控制轧制与控制冷却、轧机设定及自动化、薄板坯连铸连轧等课程教学。近10年发表论文20篇,其中被EI检索4篇,被SCI检索2篇。近年来作为项目负责人完成和正在承担企业横向合作课题2项,参与湖北省自然科学基金课题1项,武钢、涟钢横向课题多项。2001年获武汉科技大学教学成果二等奖“金属材料加工工程专业课实验教学体系研究”;2005年获湖北省科技进步二等奖“硬线显微组织与性能预报研究”;2008年获湖北省科技进步二等奖“CSP冷轧薄板产品系列及深冲性能开发研究”;2010年获发明专利“硬线显微组织与性能预报研究”1项。主要研究方向:轧制过程计算机控制、轧制过程冶金学与轧材品种开发、连铸连轧新技术等。