有限元在自然电位测井中的应用

孔 峰, 朱泰英

(上海电机学院数理教学部,上海200240)

有限元在自然电位测井中的应用

孔 峰, 朱泰英

(上海电机学院数理教学部,上海200240)

针对自然电位(SP)测井的正问题,研究了有限元方法在求解数值解中的应用。通过构造新函数的方法,将一个不能使用有限元计算的问题化为一个可用标准的有限元方法来求解的问题,并对非齐次项进行了分析,选取了适当的构造函数,提高了计算精度。

自然电位;测井;有限元

Abstract：We study application of finite element method to obtain numerical solution to the problem of spontaneous potential well-logging.By constructing a new function,we convert the problem to a new form that can be solved by the standard finite element method,and analyze an inhomogeneous term and choose an appropriate constructor to improve accuracy.

Key words:spontaneous potential(SP);well-logging;finite element method(FEM)

自然电位(Spontaneous Potential,SP)测井是一种被广泛应用于现代石油勘探中的测井方法。SP测井所用的测量工具包括一个放在井眼中的可移动电极和一个放在地面泥浆槽中的参考电极。通过变换可移动电极的位置,绘制出井轴上的自然电位曲线图,不同的电位曲线反映出不同的地层信息。为了制作相应的测井解释图表,通常假设地层信息中各子区域的电阻率以及交界面上的电势跳跃都是已知的。井轴上的自然电位u=u(r,z)满足在交界面上有跳跃的椭圆边界值问题。在结合点 A和B处(见图1),自然电位的跳跃不满足相容性条件,这就找不到一个分片 H1的解,也就不能直接用标准的有限元方法求解[1]。本文通过构造新函数的方法将由不满足相容性条件导致的奇性化到了方程的右端,从而可以利用标准的有限元方法求解。

1 问题陈述

1.1 数学模型

通常假设地层是关于井轴和中心平面对称的[2],在平面(r,z)的区域中考虑问题,其中 R,Z是适当大的数。假设电阻率 Re是分片常数[3](见图1),则

式中,Ωm为被泥浆充满的井陉;Ωs为围岩;Ωx0为侵入带;Ωt为目标层。

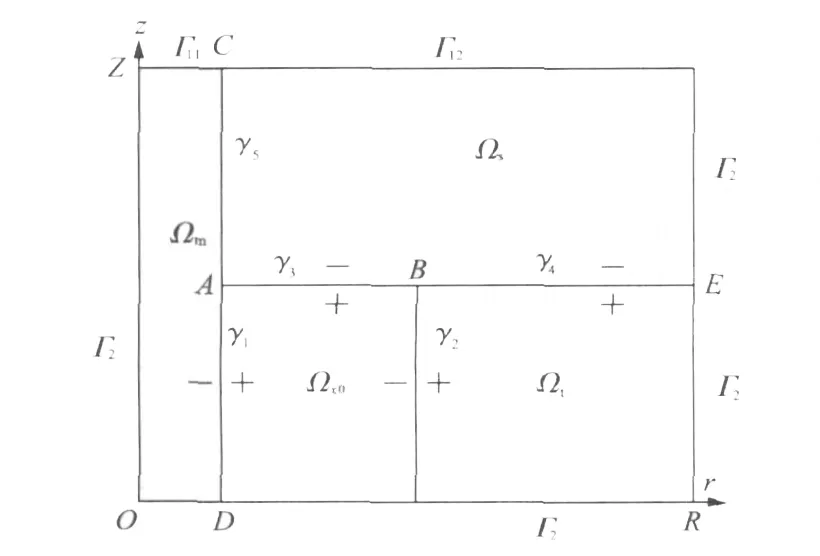
图1 井轴横切面示意图Fig.1 Axial cross-section of the well

因为Ωt由渗透性的砂层组成,泥浆滤液会侵入到这个多孔的区域并改变区域Ωx0的电阻率,所以Ωx0通常叫做侵入带[4]。

在实际问题中,区域半径 r→+∞,而一般只用一个有限的R来近似。这种近似的合理性在文献[5]中得到了证明:当 R-Dx0/2≥Z,R>2Dx0时,近似值和实际值的相对误差量级为o(10-4)～o(10-8),并且在均匀地层中取R和Z大小相等较合适。

在正问题中,自然电位函数 u(r,z)在Ωi(i=1,2,3,4)中满足如下的拟调和方程[1]:

在各个边界和交界面γi(i=1,2,…,5)上满足如下的边界条件:

式中,Ei为γi上的电位差。

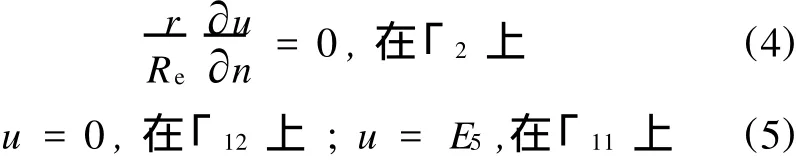
1.2 问题化简

作

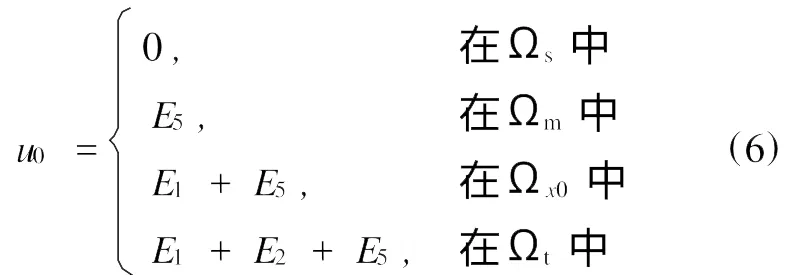
并作变换[6]

则v满足一个新的边界值问题:

新闻传播学、戏剧影视学两个学科都具有中国传媒大学的独到优势和特色。首先体现在“综合”。新闻传播学起步于广电，随着中国整个媒体行业的快速发展，从广电延伸到电子媒体，再从电子媒体延伸到视听新媒体、融媒体。戏剧影视学也大致如此，起步是电视艺术，电视艺术后来延伸到视觉艺术，又延伸到影视行业，最后将戏剧和戏曲也纳入其中。第二个特点就是“交叉”。新闻传播学、戏剧与影视学不仅载体、平台有交叉，艺术、技术也有交叉。特别是这几年大数据、智能媒体的兴起，使它们的覆盖领域更加宽泛。交叉、融合肯定是未来方向，需要开启新闻传播学、戏剧影视学的新视野和新维度，促进学科建设与发展的良性循环。

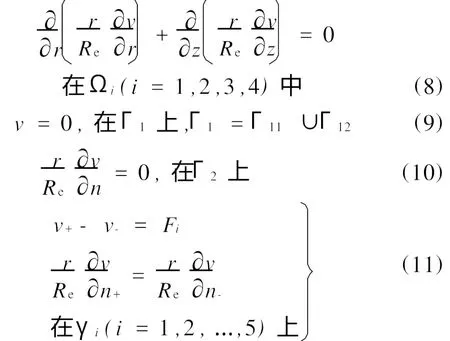
式中,F1=F2=F5=0;F3=E3-E1-E5;F4=E4-E1-E2-E5。

新问题v在Γ1上满足一个零边界条件,在垂直交界面是连续的。如果在点 A和B处的自然电势差的代数和为0,即

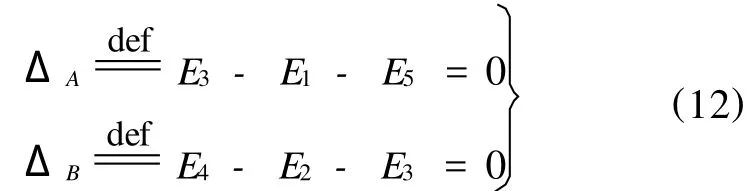
就有 F3=ΔA=0,F4=ΔA+ΔB=0,于是 v≡0。故u0就是初始问题式(2)～式(5)的分片光滑的解[7]。在这种情况下,自然电势差被称为是相容的。然而在实际问题中,通常所遇到的问题都是相容性条件不满足的情形。在这种情况下,不可能得到一个分片 H1的弱解。但是,对于任意的 p(1≤p<2)可以得到一个分片W(1,p)的解[8]。

2 问题分析

在相容性条件不满足的情况下,正问题没有一个分片 H1的弱解,不能直接用有限元方法求解。对交界面的点A和B进行分析,边界结合点处电位差的不相容性导致了正问题的奇性。构造函数

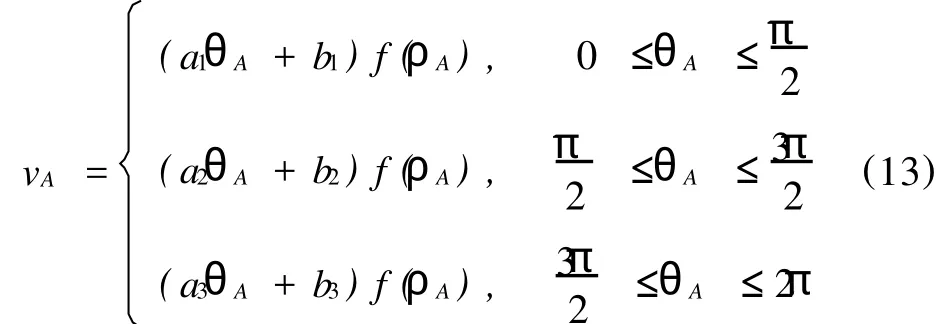
式中,ai,bi(i=1,2,3)为待定系数;θA为A点处的极角;ρA为A点处的极径。f(ρA)∈C∞且满足

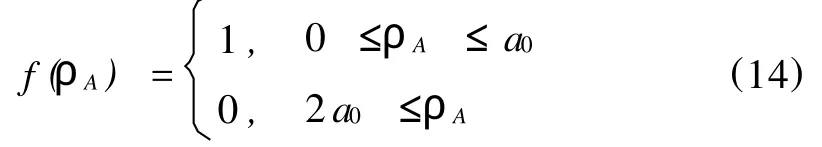
式中,a0为一个充分小的正常数,它满足2a0≤min(|OD|,|AB|,|A C|,|A D|)。选取适当的 ai与bi,使 vA满足

类似地构造 vB。

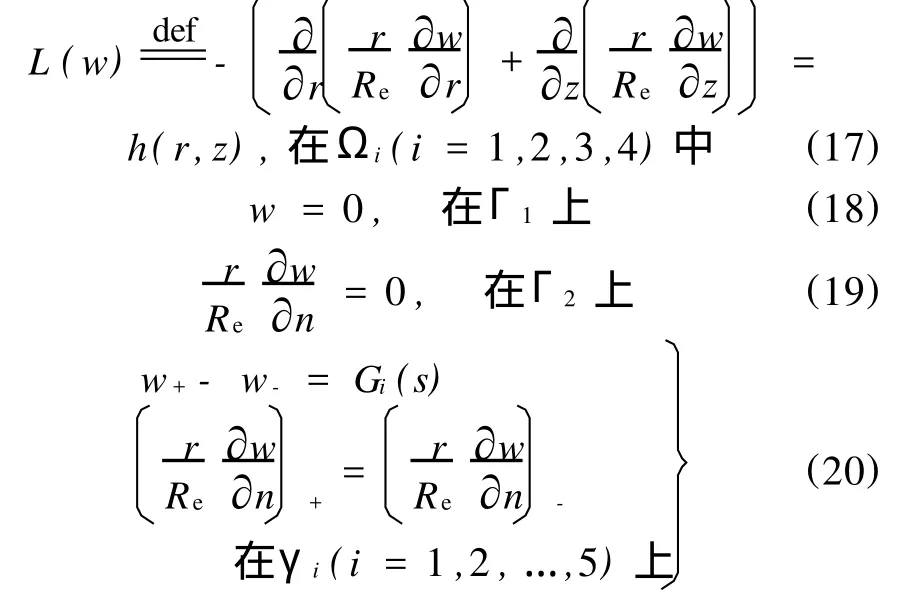
式中,h(r,z)=L(vA)+L(vB);s为弧长;Gi(s)为电势跳跃。

Gi(s)是Lipschitz连续并且满足相容性条件的,从而可以用标准有限元方法求出它的数值解。

3 有限元方法

3.1 数值结果

为了检验上面的数值方法,对一种比较经典的情形进行了计算。假设地层是均匀的,并且是无限延伸的,即 Rm=Rx0=Rt=Rs,此时井轴上的电位值具有“精确解”的表达式[6]为

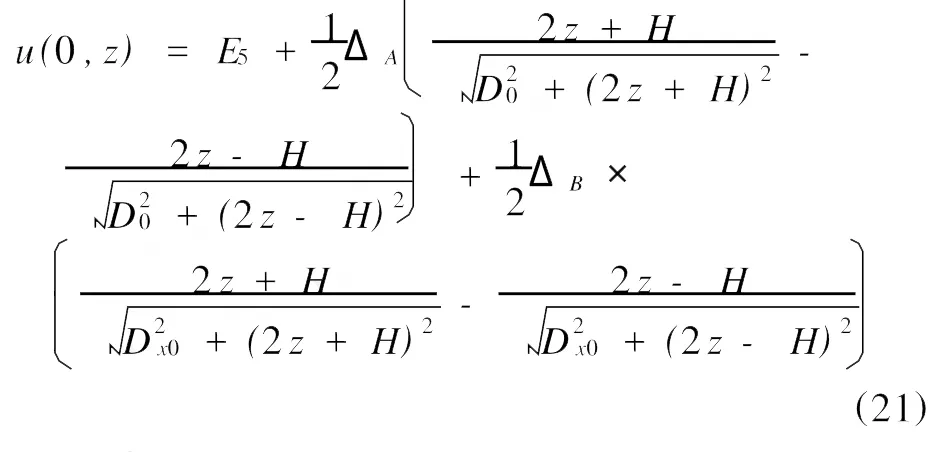
对于H=4 m,D0=0.25 m,Dx0=1.3 m,E1=20 mV,E2=130 mV,E3=130 mV,E4=130 mV,E5=10 mV的情形分别用差分法和有限元素法进行计算,并比较结果。图2是用有限元素法得到的自然电位曲线图与“精确解”的比较,表1是在不同的方法下得到的自然电位值与“精确值”的比较[9],z为深度。

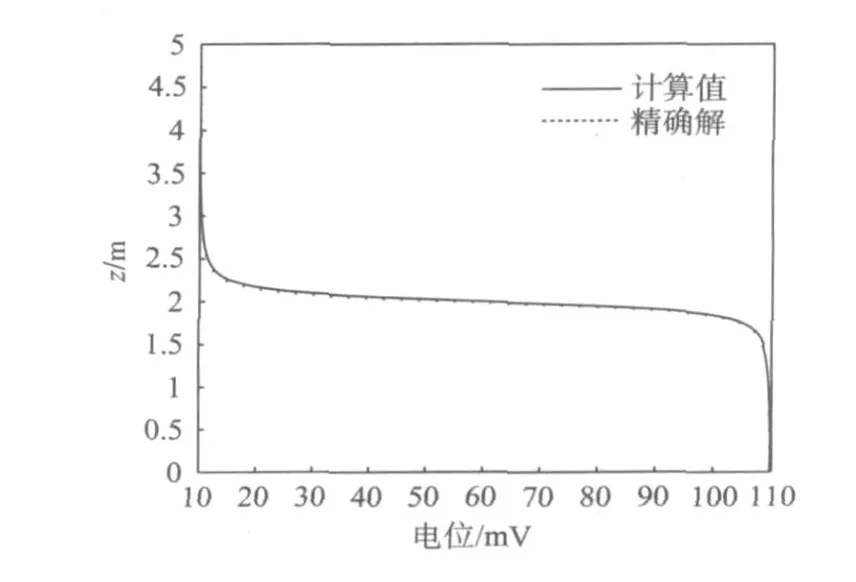
图2 自然电位曲线比较图Fig.2 Spontaneous potential curve

3.2 有限元方法的改进

有限元的一般方程为

式中,S为一个稀疏矩阵;X为每个节点处的电位值所构成的向量;J为每个节点处电位积分值。

网格剖分直接决定着式(22)左端项,不同的网格剖分对应着不同的稀疏矩阵。测井正问题所对应的稀疏矩阵是一个带状矩阵[7],不同的网格剖分只影响少数边界点所对应的元素,不影响矩阵的带宽和性质,从而不影响计算的精度[10]。而对于式(22)右端积分项,需要构造光滑函数 f(ρA)和 g(ρB),并在较小的直角三角形区域上进行积分,不同的 f(ρA)和 g(ρB)对应着不同的右端项。由稀疏矩阵的性质知,f(ρA)和 g(ρB)的选取直接影响着计算精度。根据式(13),实际计算时只用到 f(ρA)和 g(ρB)的一阶和二阶导数,故可以用二次或者更高次的多项式来近似表示它们[9]。对于多项式的次数m取不同值时,电位计算值与“精确解”的相对误差ε结果列于表2中。

由表2可知,当多项式取 m=4时,计算精度最高。

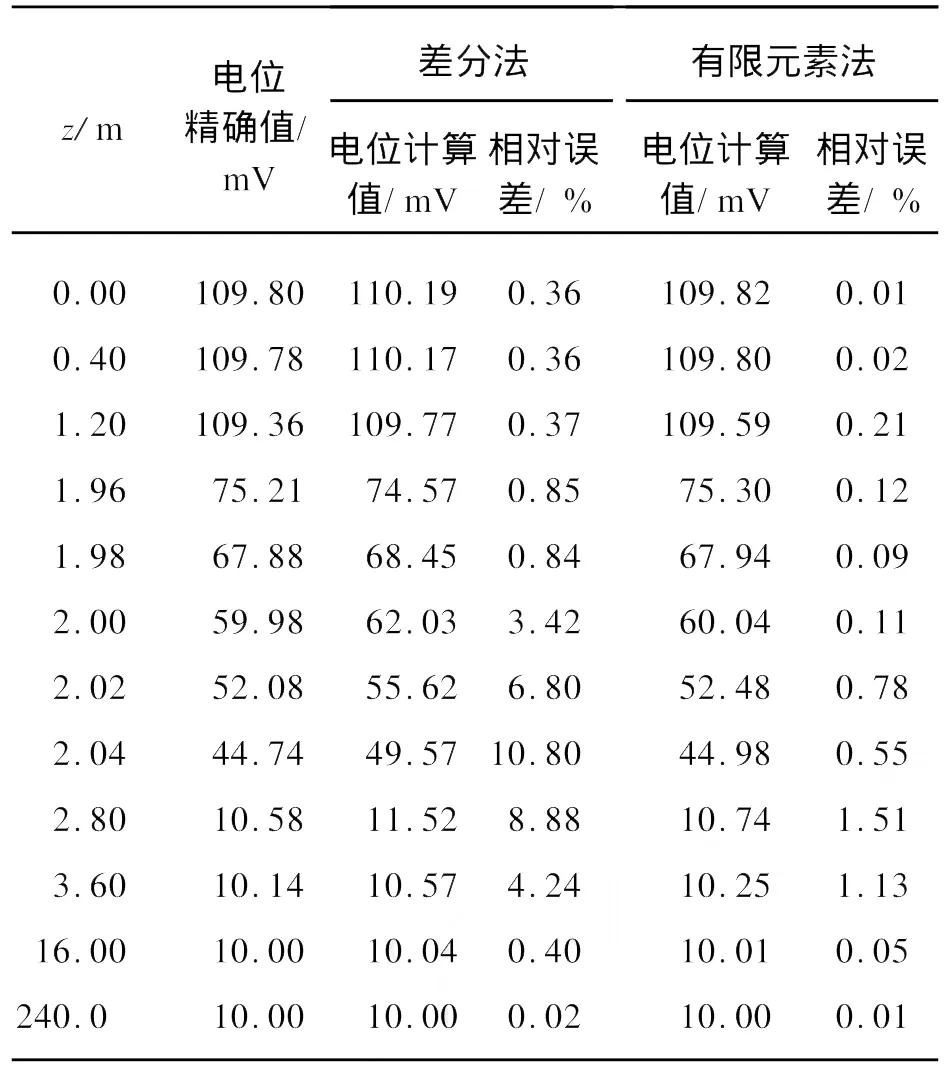
表1 井轴上自然电位值的比较Tab.1 Spontaneous potential on the well axis

表2 m取不同值时电位计算值与“精确解”的相对误差Tab.2 Relative error for different m

4 结 语

具有跳跃边界条件的拟调和方程在不同边界的交界点处,跳跃条件是不相容的,导致此类方程不能直接用有限元方法求解。本文通过构造一个在交界点处具有奇性的新函数将原方程化为一个非齐次方程,从而可利用标准的有限元方法求解。这种将边界条件的奇性化到方程中去的方法可以推广到调和方程等其他具有相同性质的方程中去,具有广泛的适用性。

[1]Li Tatsien,Tan Yongji,Peng Yuejun.Mathematical model and method for spontaneous potential well-logging[J]. European Journal ofApplied Mathematics,1994,5:123-139.

[2]潘克家,谭永基.复杂地层中自然电位测井的高效数值模拟[J].石油地球物理勘探,2009,44(3):371-376.

[3]李 宏.高分辨率间断有限元方法[J].计算物理,2004,21(4):367-376.

[4]潘克家,谭永基,胡宏伶.非均质地层中自然电位测井的数学模型和数值方法[J].应用数学和力学,2009,30(2):204-212.

[5]李海龙.均匀地层中自然电位测井方程的“精确解”[J].数学年刊,1996,17A(1):87-96.

[6]陈 华,潘克家,谭永基.核磁共振弛豫信号多指数反演新方法[J].测井技术,2009,33(1):37-41.

[7]Li Tatsien.A class of non-local boundary value problems for partial differential equations and its applications in numerical analysis[J].Journal of Computational and Applied Mathematics,1989,28:49-62.

[8]潘克家,谭永基,王才经.自动识别油藏边界水侵量微分方程反演算法[J].石油学报,2008,29(5):747-751.

[10]王文娟,潘克家,曹俊型,等.基于 Tikhonov正则化的双频电磁波电导率成像反演[J].地球物理学报,2009,52(3):750-757.

Application of FEM in Spontaneous Potential Well-logging

KON G Feng, Z HU Taiying
(Department of Mathematics and Physics,Shanghai Dianji University,Shanghai 200240,China)

O 241.82;TD 173

A

2095-0020(2010)04-0232-04

2010-06-13

国家自然科学基金项目(10871130)

孔 峰(1985-),男,助教,专业方向为应用数学,E-mail:kongf@sdju.edu.cn