两种常用橡胶本构模型的有限元分析及其仿真

殷 闻, 靳晓雄, 仝 光,2

(1.同济大学汽车学院,上海201804;2.上海电机学院汽车学院,上海200245)

两种常用橡胶本构模型的有限元分析及其仿真

殷 闻1, 靳晓雄1, 仝 光1,2

(1.同济大学汽车学院,上海201804;2.上海电机学院汽车学院,上海200245)

在分析了3类常用橡胶材料本构模型的基础上,对两参数Mooney-Rivlin模型和3次Yeoh模型的材料参数进行了数学计算。采用MSC.Marc非线性有限元分析软件对三维哑铃状试样进行不同载荷水平下的单轴拉伸试验仿真,验证模型的适用性,为进一步研究打下理论基础。

橡胶材料;本构模型;应变能函数;非线性有限元

Abstract：Based on an overview of three rubber constitutive models,we calculate material parameters of the Mooney-Rivlin model and the third order Yeoh model.We carry out simulation of a 3D-dumbbell specimen uniaxial tensile test under different load levels using MSC.Marc,which is software for nonlinear finite element analysis,and analyze the two models'stress.The results verify applicability of these models and provide a theoretical foundation for further research.

Key words:rubber material;constitutive model;strain energy function;nonlinear finite element

橡胶作为一种超弹性材料,表现出与金属材料截然不同的物理化学性能。其在工程中应用广泛,主要用来减振、密封等。与金属材料相比,橡胶材料的应力-应变关系表现出明显的非线性,使得对橡胶力学行为的描述变得复杂。因此,合理地选择橡胶材料的本构模型就变得十分重要。本文在概述多种本构模型的基础上,选择两种常用的本构模型,即两参数Mooney-Rivlin模型和3次Yeoh模型对橡胶材料进行有限元计算,并对结果进行了对比分析。

1 橡胶材料的本构模型概述

常用的橡胶材料本构模型主要分为3类:①基于分子统计学理论的本构模型;②以应变不变量表示的应变能密度函数;③以主伸长率表示的应变能函数。

1.1 基于分子统计学理论的本构模型

分子统计学理论把橡胶弹性体看成是一个由任意取向的柔性长链分子通过交联点组成的分子链网络,分子链末端距的径向分布符合高斯函数。该理论认为,橡胶材料的应力应变行为主要取决于构象熵。研究表明:当没有外力作用时,分子链的构象熵趋于最大值;而当有外力作用时,由于分子链内的旋转运动,使得构象数发生变化,从而导致构象熵也发生变化。这种构象熵的变化使得橡胶材料具有了高弹性[1]。若分子链由 n个长为l的链节组成,链节末端距向量为 r0,若,则可采用 Gauss统计理论来建立本构模型[2]。常用的分子统计学模型包括 Neo-Hookean模型,Kuhn-Grun模型以及 Arruda-Boyce模型。

1.2 以应变不变量表示的应变能密度函数

工程上处理橡胶弹性问题时,大都认为橡胶材料是各项同性的,故橡胶材料的变形可以看成是均匀变形。应变能密度函数可以表示成主伸长率λi,或者是Cauchy-Green应变张量不变量 I1,I2和 I3的函数。又因为弹性体一般近似认为是不可压缩的,即体积比 J=1,故 I3常取为1.0[3]。应变能密度函数在工程上,特别是超弹性体的变形研究中应用广泛。其中,Mooney于1951年提出了以 I1,I2为变量的应变能表达式

式中,Cij为材料常数。

当取前两项时,应变能表达式为式(2)即为两参数Mooney-Rivlin模型,工程上常用该模型来研究弹性体的变形,它能较好地模拟橡胶材料的中小变形行为。在此基础上,众多学者根据自己研究对象的不同,提出了适合各自研究对象的高阶 Rivlin应变能函数。其中,Yeoh提出了一个仅以 I1为变量的3次应变能函数:

式中,C10,C20和 C30为与温度有关的材料参数。

Yeoh模型能描述随变形而变化的剪切模型的填料橡胶,而且由某种简单变形实验数据拟合出的参数可以用来预测其他变形方式的力学行为,描述的变形范围也较宽,一般适合于模拟大变形,但是它不能很好的解释等双轴拉伸实验。

1.3 以主伸长率表示的应变能函数

在有限元分析中,Ogden模型是较常用的以主伸长率表示的应变能函数。其应变能函数的表达式为

式中,μn,αn为与变形无关的材料常数。

事实上,Ogden模型与 Mooney-Rivlin模型并没有本质上的不同。在有限元分析中,选择哪一个模型仅仅在于系数拟合是否方便。

2 本构模型材料参数的数学计算

橡胶本构模型的材料参数对有限元的计算结果影响很大,即使对于同一个本构模型,选择不同的材料参数也会得到不同的计算结果。以下介绍两种工程中常用的橡胶本构模型材料参数的计算方法。

2.1 两参数Mooney-Rivlin模型

橡胶类材料的应力-应变关系可由应变能密度函数得到,其一般形式为[4]

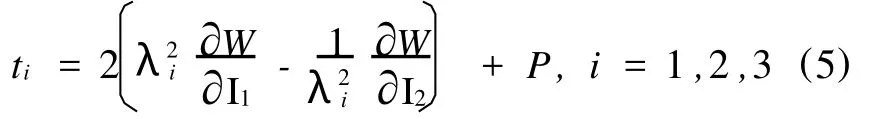
式中,P为一个未知的压力,反映了橡胶是不可压缩及对压力不敏感的事实。

在单轴拉伸试验状态下,拉伸比定义为λ22=λ23=1/λ1,并假定 t2=t3=0。则在拉伸过程中,材料体积保持不变,满足不可压缩条件。将上述关系式代入相应于t2和t3的式(5),可求得

将式(6)代入t1的表达式,可得单轴拉伸试验中柯西应力的表达式为

将两参数Mooney-Rivlin应变能密度函数W代入式(7),有

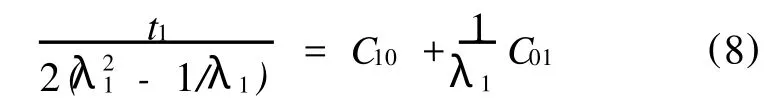
根据橡胶材料的单轴拉伸试验测得的形变和应力数据[5],令,则C01,C10为由数据点拟合而成的直线 y=C01x+C10的斜率和截距。由上述方法可以拟合得到两参数Mooney-Rivlin模型的材料参数 C10和 C01。其值分别为1.2和-0.33。

2.2 3次Yeoh模型

将3次 Yeoh应变能密度函数 W代入式(7),有

令x=2(I1-3),,则式(9)可化为y=C10+C20x+0.75C30x2。

故 C10,C20和0.75C30为抛物线一般式的3个系数。由橡胶材料的形变和应力数据,通过MATLAB编程可以得到 C10=0.897 8,C20=-0.057 8,C30= -0.053 3。

3 基于MSC.Marc的有限元仿真

3.1 模型的几何特征及约束条件

为了验证两种本构模型的适用条件及范围,本文通过建立一个三维哑铃状试样模型来模拟单轴拉伸的过程。假设模型在拉伸过程中体积保持不变,满足不可压缩条件。模型剖面结构尺寸如图1所示[6]。

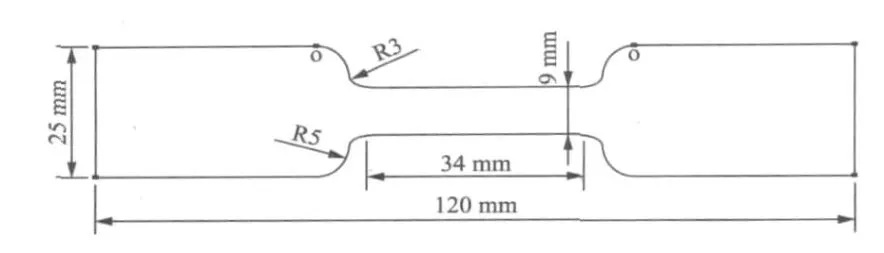
图1 三维哑铃状试样剖面结构尺寸Fig.1 Sectional dimension of dumbbell spcimen

单元类型采用 Herrmann84号单元,单元总数为14 848个。为了保证在有限元分析过程中不会因为单元畸变而导致运算终止,在 Hypermesh中设置单元密度为1.0[7]。将哑铃状试样两端约1/5的节点除 x方向位移外的其余5个自由度全部约束,并约束一个端面上 x方向的位移,同时在另一个端面上施加固定载荷。

图2 载荷水平为23 N时两模型Von Mises应力云图Fig.2 Von Mises stress contours of the two models

3.2 有限元仿真结果

本文采用MSC.Marc非线性有限元分析软件对三维哑铃状试样进行不同载荷水平下单轴拉伸试验的仿真[8]。橡胶材料的本构模型分别选用两参数Mooney-Rivlin模型和3次 Yeoh模型,材料参数由前文所述的方法得到。在不同载荷水平下,仿真得到对应于两种本构模型的三维哑铃状试样的Von Mises应力云图和位移云图。图2和图3所示为载荷水平为23 N时的仿真的结果。

由图2可见,最大应力值出现在试样受拉端的截面尺寸变化处,此处虽然做了倒角处理,但由于曲率的变化,仍然会有应力集中的现象存在。

图4和图5是各载荷水平下的Von Mises应力曲线和位移曲线。由图4和图5可见,当载荷较小时,由于橡胶材料的力学响应较小,相应地,由两种本构模型计算得到的应力和位移其差值也较小。而随着载荷的增加,两种本构模型对应的应力差值和位移差值逐渐变大。当载荷超过23 N时,应力差值和位移差值均超过 10%,且 3次

Yeoh模型的位移比两参数 Mooney-Rivlin模型的位移增加得更快。

图3 载荷水平为23 N时两模型位移云图Fig.3 Displacement contour of the two models

图4 不同载荷水平下的 Von Mises应力曲线Fig.4 Von Mises stress curve under different load levels

4 结 语

本文通过数值分析的方法,对两参数Mooney-Rivlin模型和3次 Yeoh模型的材料参数进行了计算。在不同载荷水平下对三维哑铃状试样进行了单轴拉伸试验仿真。验证了两种模型的适用性。由前述分析可见,相对于3次 Yeoh模型来说,两参数Mooney-Rivlin模型能更好的模拟橡胶的中小变形行为。

图5 不同载荷水平下的位移曲线Fig.5 Displacement curve under different load levels

[1]谭江华,罗文波.橡胶材料分子链网络本构模型的研究进展[J].材料导报,2008,22(7):31-34.

[2]朱艳峰,刘 锋,黄小清,等.橡胶材料的本构模型[J].橡胶工业,2006,53(2):119-125.

[3]李晓芳,杨晓翔.橡胶材料的超弹性本构模型[J].弹性体,2005,15(1):50-58.

[4]Gent A N.Engineering with rubber:how to design rubber components[M].New York:Oxford University Press,1992.

[5]黄建龙,解广娟,刘正伟.基于 Mooney-Rivlin模型和 Yeoh模型的超弹性橡胶材料有限元分析[J].橡胶工业,2008:55(8):467-471.

[6]何春明,郑慕侨.测定橡胶Mooney-Rivlin模型常数的一种新方法[J].北京理工大学学报,1997,17(2):142-146.

[7]蒋学武,吴新跃,朱石坚.综合应用UG,HyperMesh和MSC Marc软件进行有限元分析[J].计算机辅助工程,2007,16(2):11-14.

[8]Qian Li,Zhao Jiancai,Zhao Bo.Fatigue life prediction of a rubber mount based on test of material properties and finite element analysis[J].Engineering Failure Analysis,2009,16(7):2304-2310.

Finite Element Analysis of Rubber Constitutive Models and Simulation

YIN Wen1, J IN Xiaoxiong1, TON G Guang1,2
(1.Automotive Institute,Tongji University,Shanghai 201804,China;2.School of Automobile,Shanghai Dianji University,Shanghai 200245,China)

TB 115

A

2095-0020(2010)04-0215-04

2010-06-21

殷 闻(1985-),男,硕士生,专业方向为汽车振动与噪声,E-mail:markyin2008@163.com