并联式踝关节康复机器人设计

印 松

(上海电机学院机械学院,上海200245)

并联式踝关节康复机器人设计

印 松

(上海电机学院机械学院,上海200245)

根据人体踝关节的运动特点,提出采用具有3个转动自由度的并联机构实现踝关节康复训练机器人。通过自由度分析,开展机构分支运动链设计,得到了3-SPS/S型并联机构。研究了机构奇异性出现的条件,奇异性分析结果表明:不同的机构结构形式,其运动学性能也完全不同。

并联机构;康复机器人;奇异性

Abstract：In this paper,a three dimension-of-freedom(DOF)parallel mechanism with pure spherical rotations is presented for ankle rehabilitation.After calculating the DOF,design of kinematical chains is carried out,leading to a 3-SPS/S parallel mechanism.Based on the kinematical analysis,three cases of singularity are discussed.The results show that different architectures may result in huge differences in kinematical performance.

Key words:parallel mechanism;rehabilitation robot;singularity

踝关节作为人体负重最大的关节,极易在日常生活和运动中发生扭伤,如果不及时加以治疗,容易造成关节不稳并引起踝关节的反复损伤,严重时患者将永久丧失正常行走的能力。临床医学表明:外力辅助下的康复训练能有效预防关节肌肉的萎缩,实现肢体和关节机能的恢复。当前,康复训练的主要方式是专业医师根据患者的病况,依靠人力或一些简单的医疗设备来实现。将机器人应用于康复领域,可以减轻医师的负担和患者的痛苦,根据患者不同的恢复期提供不同的康复训练方案,提高了康复训练的效果,故康复机器人技术正逐渐成为国内外研究的热点[1]。

从运动形式来看,踝关节可视为具有3个转动自由度的球铰。目前,临床使用的踝关节康复训练器结构简单,功能单一,且仅提供一个方向上的转动(背伸/跖屈),因此康复训练并不全面。由于并联机构具有高刚性、高承载能力等特点,能以紧凑的结构实现多个自由度,故在数控机床、医疗设备和运动模拟器等众多领域得到应用。近年来,国内外科研工作者开展了基于并联机构的踝关节康复训练机器人的应用研究。美国新泽西州立大学研制的Rutgers踝关节康复训练器采用一个6自由度的Stewart平台来帮助患者实现踝关节的康复训练[2]。Tsoi等[3]人提出基于3自由度并联机构的踝关节康复训练器,并采用冗余驱动的方法来消除机构工作空间中的奇异性。Saglia等[4]人将踝关节简化为具有2个转动运动的铰链,并采用2自由度的并联机构来实现踝关节康复训练器。赵铁石[5]、何春燕等[6]人以3-RSS/S型3自由度并联机构为基础,开展了踝关节康复机器人的研究。

本文以踝关节康复机器人的设计为出发点,研究3转动并联机构分支运动链的结构形式,并以3-SPS/S型并联机构为例进行运动分析和奇异性分析。

1 踝关节康复机器人机构设计

如图1所示,人体踝关节可视为球面副,它可以实现背伸/跖屈、内翻/外翻以及绕小腿轴线的内旋/外旋3个转动,一个紧凑、完整的踝关节康复机器人机构应具备提供这3个运动的能力。

图1 踝关节运动模型Fig.1 Kinematics of human ankle

简单的单自由度转动铰链难以满足踝关节对运动自由度的需求,而复杂的串联式机构不但增加了结构的复杂性,往往还难以达到设计目标[7]。由于并联机构具有高刚性、高承载能力等优点,且能以紧凑的结构实现多个自由度,故考虑采用并联机构设计踝关节康复机器人。假定并联机构满足:①机构原动件数等于机构末端执行器自由度数,即原动件数为3,机构既非欠驱动,也非冗余驱动;②每个分支运动链仅含1个原动件,即分支运动链数为3;③各分支运动链具有相同的结构形式;④分支运动链沿圆周方向均匀分布;⑤机构动平台与静平台之间通过一个S(球面副)运动链连接,以保证机构实现绕定点(球面副中心点)的3个转动自由度。假定各构件之间通过单自由度的基本副连接,根据 Kutzbach Grubler公式[8],该并联机构满足

可得

式中,F为机构自由度数,F=3;λ为机构所处空间的维数 ,λ=6;n 为构件数 ,n=3n′+2,其中 n′为单个分支运动链所具有的构件数;g为运动副数,g=3g′+1,其中 g′为单个分支运动链所具有的运动副数;fi为第i个运动副的相对自由度数。

由式(1)可知,并联机构每个分支运动链需包含6个单自由度简单副或等价的多自由度运动副。然而,对并联机构这类复杂的空间机构,必须考虑各分支运动链构件和约束的类型、方向等因素对自由度计算公式所产生的影响[9]。为了消除分支运动链的影响,选用一种具有零终端约束的运动链——SPS运动链,该运动链包含2个3自由度的球面副和1个单自由度的移动副[9]。采用SPS运动链的3自由度纯转动并联机构如图2所示。

图2 3-SPS/S型纯转动并联机构Fig.2 3-SPS/S rotational parallel mechanism

图2中,P为主动副,提供驱动力,可通过任何直线运动构件来实现(如直线电机、气缸、液压缸等),机构末端执行器绕中间球面副转动,模拟踝关节的背伸/跖屈、内翻/外翻和内旋/外旋运动。

2 机构运动学分析

对其中一个分支运动链进行分析,由空间矢量关系可得

式中,li为点Bi指向点 Pi的向量;pi为点O指向点 Pi的向量,为末端执行器位姿的函数;bi为点O指向点Bi的向量。

对应于末端执行器给定的位姿,驱动器的输入可表示为

对式(2)两端求导,得 Pi点速度关系式为

式中,ω为动平台相对于静平台的角速度向量。

将式(4)沿运动链轴线方向投影,可得如下速度关系方程:

式中,ei为沿分支运动链的单位向量。

将式(5)所表示的3个方程写成矩阵的形式,有

式中,J为将操作速度映射到驱动器输入速度的雅可比矩阵。

3 机构奇异性分析

奇异性是制约并联机构广泛应用的一个重要因素,与串联机构不同,并联机构的奇异点可能出现在其工作空间中的任意位置,甚至整个工作空间。在奇异位置处,机构自由度可能发生突变,出现过输入或不可控现象,故给机构的设计、运动规划与控制带来很大的困难。在进行踝关节康复训练机器人设计时,应研究满足奇异性的结构条件,避开可能造成机构奇异性的结构形式。

并联机构的奇异性条件通常由其雅可比矩阵给出,当雅可比矩阵的行列式等于零时,机构处于奇异位置,即

也即,向量 p1×e1,p2×e2和 p3×e3之间存在相关性,具体分析如下。

(1)当 pi×ei=0时,向量 pi与 ei重合,即转动中心O与Bi或Pi重合。假定O与点P1重合,当驱动器全部锁死时,机构仍存在绕平面 P1P2B2和平面 P1P3B3的交线瞬时转动的可能。同样,假定O与点B1重合,机构存在绕平面B1P2B2和平面B1P3B3的交线瞬时转动的可能。

(2)当 pi×ei与 pj×ej线性相关,其中 i≠j。假定 p1×e1与 p2×e2线性相关,此时,点 B1,P1,B2,P1,O处在同一平面内,机构存在绕过 O且沿p1×e1方向直线的瞬时转动。

(3)当 p1×e1,p2×e2和 p3×e3位于同一平面内。此时,机构存在绕过O且与该平面垂直的直线的瞬时转动。典型情况包括:①当e1=e2=e3时,各运动支链相互平行,向量 p1×e1,p2×e2和 p3×e3位于与运动支链垂直的平面内;②当各运动支链汇交于一点时,如图3所示,各运动支链汇聚于点O′。由于向量 p1×e1垂直于 OP1和 P1O′,因此也必然垂直于 OO′,同理向量 p2×e2和 p3×e3也垂直于OO′,机构存在绕OO′的瞬时转动。

图3 运动支链汇聚于一点Fig.3 Kinematic chains converge at one point

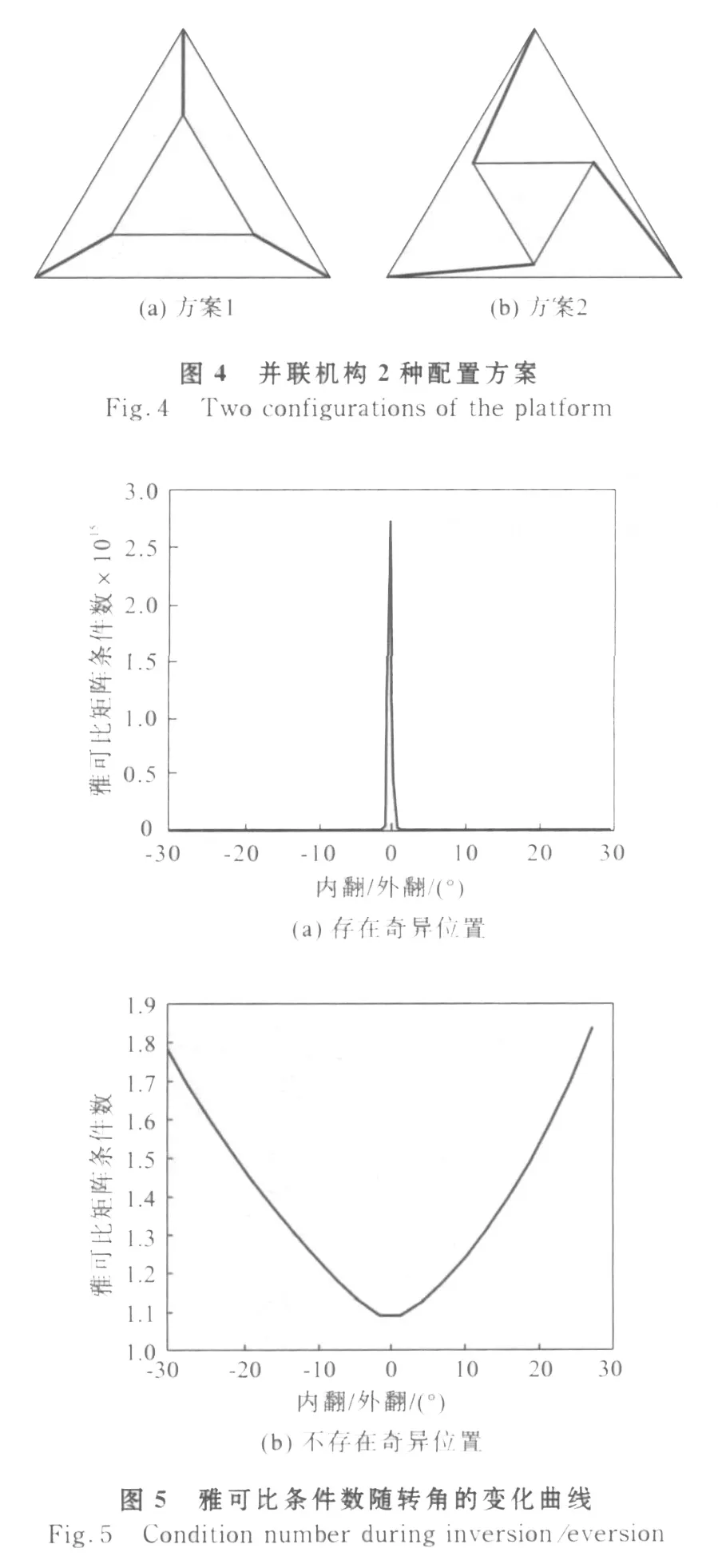
奇异性分析对机构的结构设计具有一定指导作用。并联机构可采用2种配置方案(见图4),其对应雅可比矩阵条件数随机构内翻/外翻运动的变化曲线如图5所示。图4(a)中,机构动静平台各边相互平行,其分支运动链延长线交于一点,由奇异性分析可知,该方案存在奇异位置(见图5(a)中角度0)。图4(b)中,动平台绕中心转过60°,由图5(b)可知其运动范围内不存在奇异位置。因此,从奇异性的角度考虑,优先选取图4中方案2。

4 结 语

针对踝关节的运动特点,采用并联机构设计踝关节康复训练机器人。所设计的3-SPS/S型并联机构具有绕定点转动的能力,模拟踝关节的背伸/跖屈、内翻/外翻和内旋/外旋运动,其分支运动链具有零终端约束。奇异性分析表明:不同的结构形式,机构具有不同的运动学性能,因而可以利用奇异性分析的结果指导并联机构的结构设计。

[1]吕广明,孙立宁,彭龙刚.康复机器人技术发展现状及关键技术分析[J].哈尔滨工业大学学报,2004,36(9):1224-1227,1231.

[2]Girone M,Burdea G,Bouzit M,et al.A stewart platform-based system for ankle telerehabilitation[J].Autonomous Robots,2001,10(2):203-212.

[3]Tsoi Y H,Xie S Q.Design and control of a parallel robot for ankle rehabilitation[C]//International Conference on Mechatronics and Machine Vision in Practice.Auckland,New-Zealand:[S.n.],2008:515-520.

[4]Saglia J A,Tsagarakis N G,Dai J S,et al.Inverse-kinematics-based control of a redundantly actuated platform for rehabilitation[J].Proceedings of the Institution of Mechanical Engineers,PartⅠ:Journal of Systems and Control Engineering,2009,223(1):53-70.

[5]赵铁石,于海波,戴建生.一种基于3-RSS/S并联机构的踝关节康复机器人[J].燕山大学学报,2005,29(6):471-475.

[6]何春燕,张小俊,张 泰,等.3-RSS/S踝关节康复并联机器人的速度各向同性分析[J].河北工业大学学报,2007,36(4):39-43.

[7]Zoss A,Kazerooni H,Chu A.On the mechanical design of the Berkeley lower extremity exoskeleton[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems.Edmonton,Canada:IEEE,2005:3132-3139.

[8]黄 真,孔令富,方跃法.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.

[9]赵景山,冯之敬,褚福磊.机器人机构自由度分析理论[M].北京:科学出版社,2009.

Design of Parallel Robot for Ankle Rehabilitation

YIN Song
(School of Mechanical,Shanghai Dianji University,Shanghai 200245,China)

TP 242;TH 112

A

2095-0020(2010)04-0211-04

2010-06-10

国家高技术研究发展计划(863)项目(2007AA041600)

印 松(1979-),男,讲师,博士,专业方向为机械电子工程,E-mail:yins@sdju.edu.cn