基于 KC的生理性精神疲劳分级的可行性研究

张连毅

(上海电机学院电子信息学院,上海200240)

基于 KC的生理性精神疲劳分级的可行性研究

张连毅

(上海电机学院电子信息学院,上海200240)

研究了不同精神疲劳状态下脑电信号的柯尔莫哥洛夫复杂度(KC),通过对8例不同精神疲劳状态下脑电信号 KC的分析后发现:脑电信号柯尔莫哥洛夫熵的波动范围与精神疲劳的状态有着明显的对应关系;利用 KC对生理性精神疲劳进行分级具有一定的可行性。

精神疲劳;脑电信号;柯尔莫哥洛夫复杂度;前额叶皮层;显著性差异

Abstract：In this paper,the Kolmogorov complexity(KC)of EEG under different mental fatigue statuses was measured.By analyzing the relationship between different mental fatigue statuses and the corresponding KC of EEG,we show that 1)the value of KC is strongly correlative with the mental fatigue state,and the value of mean KC corresponding to a special mental status fluctuates within the special range;and 2)it may be possible to differentiate different mental fatigue level objectively according to the KC value.

Key words:mental fatigue;electroencephalogram(EEG);Kolmogorov complexity(KC);prefrontal cortex;significant difference

疲劳是一种自我感觉[1]。生理性精神疲劳是一个包括由精神和体力活动引起的思维活动性能衰退的专业术语[2]。Linden等[3]人将精神疲劳定义为由于维持某一性能而引起的生理与心理状态的变化,这些变化中有主观方面的,也有客观方面的,包括继续努力时难度的增加、信息分析能力下降趋势的增强,以及心情的变化等。按照上述的精神疲劳定义,所维持的某一性能并不一定局限在同一任务中,还可在需要付出精神劳动的不同任务中,如在办公室工作而引起的精神疲劳。在有认识要求的任务中,工作一定时间常常导致精神疲劳,而精神疲劳会影响人们的思维活动。在现代工业中,尤其是实时监控、车辆驾驶、航空航天、高风险作业等行业,许多事故的发生都与精神疲劳有关。因此,认识精神疲劳的本质及精神疲劳对人们精神活动的影响,对于预防由精神疲劳引发的事故是十分重要的。人的生理性精神疲劳是非常复杂、非常难以客观检测的。近年来,有关生理性精神疲劳的研究已取得了一定的进展[4-6]。

脑电信号复杂度测量是近年来发展起来的一种新方法,它可以定量评价直观的信号曲线变化的复杂性,有效地反映大脑在生理、病理和不同药物作用下的某些变化特征[7-8],便于各种大脑活动间的比较和区分。算法复杂度又称柯尔莫哥洛夫复杂度(Kolmogorov Complexity,KC)是常用的信号复杂度计算方法之一,该方法的计算结果与信号幅值的大小无关。本文旨在研究各种疲劳状态及与其对应脑电信号的 KC之间的关系,利用KC复杂度研究精神疲劳状态变化过程的一些特征及规律,以期有助于对精神疲劳的认识与了解。

1 Kolmogorov复杂度

Kolmogorov认为,波形的复杂性可以用一串符号的复杂性替代,而一个符号序列的复杂性可定义为能够重现这一序列的程序的最短长度。一般认为描述事物的计算机语言的长度越长,则该事物越复杂;但从动力学的观点来看,稳态、周期或准周期运动都是有序的,并不复杂,而当动力系统的运动进入混沌时就变得复杂了。这种复杂程度的定量刻画十分重要,根据 Kolmogorov熵理论,给定[0,1]序列的复杂性是由产生该序列的最短计算机程序的比特数决定的,1976年,Lempel等[9]人在信息理论的研究中对随机序列的复杂性给出了定义。1987年,Kaspar等[10]人对于随机序列Lempel-Ziv意义下的复杂性进行了研究,并提出了随机序列复杂性测度的算法。该算法的实质是不断比较某一字符串是否为另一字符串的子串,若是,则复杂性测度维持不变;若不是,则复杂度测度加1。本文采用了Lempel-Ziv算法,具体使用过程如下:

(1)采用二值化法对预处理后的脑电时间序列信号进行粗粒化处理;

(2)对重构形成的[0,1]序列 S={S1,S2,…,Sn},按Lempel-Ziv算法进行比较和添加,得到各个子串的界定;

(3)计算重构序列的复杂度c(n);

(4)进行归一化。

为获得不依赖于序列长度的复杂度,需将c(n)归一化,用 C(n)来测度时间序列的复杂性变化,C(n)为反映被测信号复杂程度的归一化度量。Lempel和Ziv对属于[0,1]的序列进行了研究,发现几乎所有的c(n)都会趋向于某一定值。设序列P的长度为n,字符串中不同种类字符的个数为α,则c(n)的上限确定为[10]

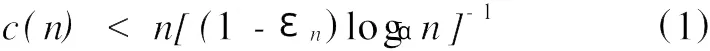
式中,εn为由因长度有限的数据串粗粒化而引起的误差。εn很小,当 n→∞时,εn→0。故 c(n)的上限为 n(logαn)-1,即

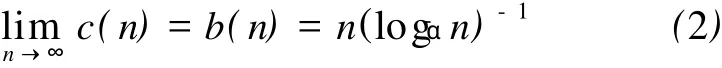
用 b(n)对 c(n)归一化,得

有规律序列的复杂度应该是0,而白噪声的复杂度最大,定义为1。对于[0,1]序列,α=2。

2 精神疲劳实验

学习或脑力劳动的持续时间、休息时间、心理因素,工作能力、劳动技巧、学习方法,营养状况及饮食情况,体质、气质、健康状况及年龄等因素,都会对生理性精神疲劳程度产生影响。环境也能够影响人们的心情和注意力,进而对疲劳产生影响。因此,生理性精神疲劳实验必须同时尽可能多地考虑上述因素对实验的影响,这涉及到受试人群的选择、导致生理性精神疲劳的原因等问题。鉴于上述考虑,本文挑选了8位受试者进行生理性精神疲劳试验,选择了安静、密闭、有电磁屏蔽、窗帘防光性能较好的实验室,在室温下(20℃左右)进行实验。

受试者均为男性,在校(住校)大学生,右利手,年龄为21～25岁;受试者均无重大脑部疾病史,参加测试的近几天内未服过任何药物与保健品。学校工作时间为9∶00～12∶00,13∶00～17∶00;学校所在地气候地理环境为热带城市。实验中只选用FP1与FP2两通道用来同步记录实验中的脑电数据。电极位置如图1所示。采用10～20导联头皮电极系统,电极放置于头部 FP1与 FP2处,各导联阻抗均小于5 kΩ,参考电极粘贴在喉结右下方的锁骨管处。脑电数据记录仪选用PL-EEG Wavepoint系统。采样间隔为6 ms。

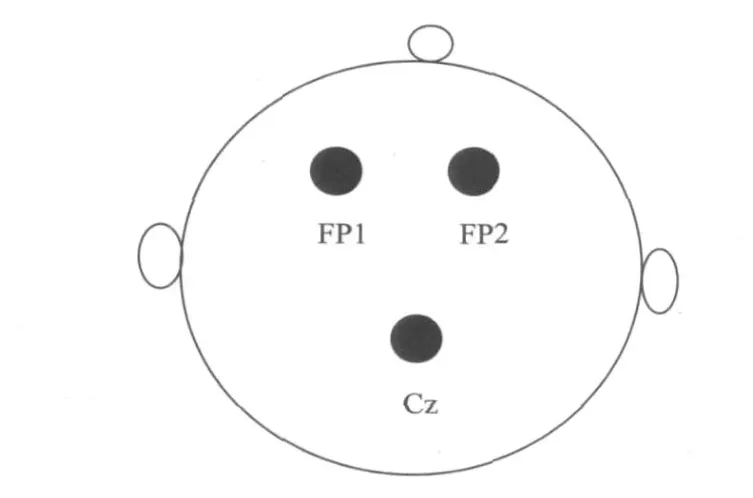
图1 电极位置分布图Fig.1 Electrode placement

本实验通过对3组不同生理性精神疲劳状态的脑电信号分析,探讨利用脑电图信号对各不同生理性精神疲劳状态进行分级的可行性。实验过程中受试者一直坐在比较舒适的椅子中,且要求受试者尽可能放松。各疲劳状态具体如下:

状态1 被试者自我感觉非常清醒。实验在室内正常照明灯光、受试者闭眼状态下进行。数据采集实验持续时间为15∶50～15∶55。

状态2 被试者自我感觉比较清醒。实验在室内正常照明灯光、受试者闭眼状态下进行。数据采集实验持续时间为17∶15～17∶20。

状态3 被试者显得有些疲劳,并偶尔打哈欠。实验时关闭室内正常照明灯光。数据采集实验持续时间为18∶52～18∶57。

3 EEG数据计算及分析

为去除脑电信号中的噪声干扰,选用了带通为0.5～30 Hz的 FIR滤波器。开始逐段计算脑电信号的 KC值时,选取2 500个采样数据(15 s内的采样数据)为分析窗长(15 s),随时间采样点不重叠地平移,计算各数据段长度(窗长)的 KC值。为减少 KC值波动的影响,先分别计算FP1与FP2两通道各数据段长度(窗长)的 KC值,再计算各时间段(窗长)内两通道的 KC值的平均值,最后取各受试者 KC的平均值,并作统计处理。

对于实验中的每一种疲劳状态,随机选取了两通道对应时间段的一段数据来分析,分别计算出每个分析窗长为15 s、连续15个窗长的 KC值。表1是3种疲劳状态下 KC值的平均值。

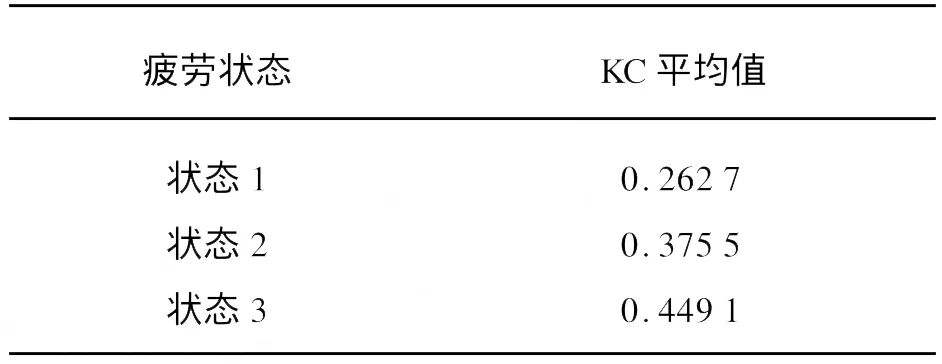
表1 3种疲劳状态下KC值的平均值Tab.1 Average KC under three different fatigue statuses

实验中,各生理性精神疲劳状态下 FP1与FP2两通道的 KC值的平均值随时间的变化曲线如图2所示。统计分析表明,3种疲劳状态间存在显著性差异(方差分析 F2,28=22.844 3,概率 P<0.01)。多重比较结果如表2所示。

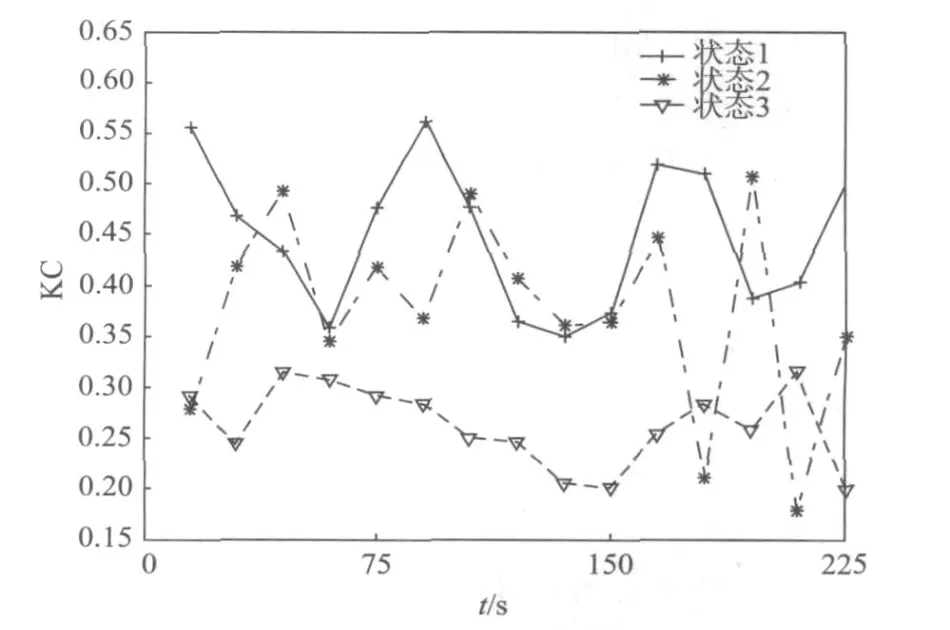
图2 各疲劳状态下 KC随时间的变化曲线Fig.2 Change of KC over time

表2 3种状态 KC的q检验比较Tab.2 Comparison between KCs of three q tests

4 结 论

从电生理学的角度来看,脑神经细胞的活动是兴奋与抑制互相作用、互相转化、互相诱导的过程。大脑在工作时,神经细胞活动相对处于比较有序的状态,随着精神疲劳程度的增加,神经对细胞活动的控制能力减弱,神经细胞活动兴奋程度增加,神经细胞活动的无序化渐趋加剧,其 KC值将会增加。

由图1与表1可以看出,主述疲劳的状态3的 KC值最大,被试者自我感觉非常清醒的状态1的 KC值最小,而被试者自我感觉比较清醒的状态2的 KC值介于状态1与由状态3之间,这与有关电生理学的先验知识相吻合;在不同生理性疲劳状态下,前额区神经电活动的复杂度各有其相应的变化范围。

从上述实验及分析中可得出以下结论:①对应于特定的生理性精神疲劳状态,其 KC值在相应的一定范围内变化,大脑思维的无序程度有特定的变化范围;随着生理性精神疲劳程度的增加,脑细胞活力下降,其KC值将随之减小。②利用 KC对生理性精神疲劳进行分级具有一定的可行性。

本文的研究结果与利用 Kolmogorov熵对其进行分级可行性的探讨性文章[3]具有很好的一致性。本文的研究方法有助于客观评估精神疲劳水平,同时也为进一步认识精神疲劳的过程、研究精神疲劳对中枢神经系统的影响提供了一种新的工具,在交通运输业及其他行业中将会有广阔的应用前景。

本文的研究方法也存在不足:精神疲劳是多因素相互作用的产物,但本方法只涉及同一脑区两对称通道的脑电数据及单一参数(KC),对于那些精神疲劳水平接近的疲劳状态,利用本方法进行识别是比较困难的;同时,由于本方法是一种非线性定性方法,在粗粒化过程中既可能忽略信号彼此之间的差异,也可能牺牲复杂信号本身的外在特征,在定量分析中会产生误差。这些都是今后研究中有待改进之处。

[1]韩绍安,许华芳.疲劳与休息[M].上海:上海科技教育出版社,1998.

[2]Meijman T F.Mental fatigue and the efficiency of information processing in relation to work times[J].International Journal of Industrial Ergonomics,1997,20(1):31-38.

[3]张连毅,郑崇勋,李小平,等.EEG柯尔莫哥洛夫熵测度用于精神疲劳状态的研究[J].中国生物医学工程学报,2007,26(2):170-176.

[4]Zhang Lianyi,Zheng Chongxun.Lempel-Ziv complexity changes and physiological mental fatigue level during differentmental fatiguestate with spontaneous EEG[J].Health,2009(1):35-38.

[5]Zhang Lianyi,Zhang Zhe,Zheng Chongxun.Study on physiological mental fatigue with nonlinear dynamics[C]//Proceedings of the 2008 Fourth International Conference on Natural Computation,4.Washington,D C.USA:IEEE Computer Society,2008:670-673.

[6]Linden D V D,Frese M,Meijman T F.Mental fatigue and the control of cognitive processes:effects on perseveration and planning[J].Acta Psychologica,2003,113(1):45-65.

[7]Grandori F,Ravazzani P.Magnetic stimulation of the motor cortex-theoretical considerations[J].IEEE Transactions on BiomedicalEngineering,1991,38(2):180-191.

[8]Esselle K P,Stuchly M A.Neural stimulation with magnetic fields:analysis of induced electric fields[J].IEEE Transactions Biomedical Engineering,1992,39(7):693-700.

[9]Ziv L J.On the complexity of finite sequences[J].IEEE Transactions on Information Theory,1976,22(1):75-81.

[10]Kaspar F,Schuster H G.Easily calculable measure for complexity ofspatiotemporal patterns[J].Physical Review:A,1987,36(2):842-848.

Feasibility of Mental Fatigue Grade Based on Kolmogorov Complexity

Z HA N G L ianyi
(School of Electronics and Information,Shanghai Dianji University,Shanghai 200240,China)

R 318.04

A

2010-05-26

国家自然科学基金项目(30670534)

张连毅(1963-),男,副教授,博士,专业方向为脑电信号分析,E-mail:zhangly@sdju.edu.cn

2095-0020(2010)04-0197-04