高等代数教法探析

黄国庆

（长治学院 师范分院，山西 长治 046000）

高等代数教法探析

黄国庆

（长治学院 师范分院，山西 长治 046000）

文章主要论述克服《高等代数》教学中的抽象性以及揭示数学的趣味的一些方法与思路。克服抽象性除了需要多思考多做题外，教师还应多利用类比法和示例法教学；揭示趣味需要挖掘和拓展教学内容，需要与一些实际例子结合。尤其结合师范生的实际情况，在教学中还应该穿插与教学有关的内容，以激发学生学习兴趣，体现数学教学的趣味性。

高等代数；数学；抽象性

《高等代数》是现代数学的基础。其学科概念性较强，相应的思维方法独特，从而造成教学存在一定的难度。笔者认为，克服其抽象性的关键在于教学中多采用类比法与示例法等方法。

1 类比法教学

高等代数是中学代数的延续与拓展，许多内容与初等数学联系比较紧密，如多项式、行列式、线性方程组、二次型等章节，在这些内容的教学中，都可以用类比法。在教学过程中，对有些知识我们经常会有“似曾相识”的感觉，而且在不同领域中会感到某种类似的成份。如果我们把这些类似进行比较，加以联想，可能发现许多意想不到的结果和方法。这种把类似知识进行比较、联想，由一个数学对象的已知性质迁移到另一个数学对象上去，从而获得另一个对象性质的方法就是类比法。类比法不仅是一种从特殊到特殊的推理方法，也是一种寻求解题思路、猜测问题答案或结论的发现方法。

教学中应充分利用学生原有的知识作为基础，让抽象的高等代数概念找到初始的原形，在类比中辨别高等代数与初等数学在处理问题思维方式上的异同。

比如，在讲解多项式的整除时，可以与数的整除类比；多项式的因式分解可以与数的质因数分解类比；在讲解线性变换时，可以与函数类比，从本质上说，线性变换是向量函数，是向量与向量之间的对应。这样对比后，更利于学生对知识的理解。又如二次型教学，可以先复习配方法，再讲二次型化为标准型的配方法。方法相同，只是配方的次数比中学时有所增加，未知量也多了，但方法本质相同。

2 示例法教学

除类比法之外，利用直观模型进行示例教学也是一种好的方法。这里的直观模型是指一个抽象问题中相关的例题或特例，且这些内容应该是已经掌握的或者容易接受的。笔者在教学中为了克服数学的抽象性，常常在讲解时穿插例题，使抽象问题具体化，以便学生们加深理解。比如在高等代数中，最抽象的概念是线性空间，历届的学生都是从这里开始感觉到课程学习的难度。我们先回顾一下数学概念的建立历史。到了20世纪，随着数学的系统化，模型的分析才受到重视。于是，出现集合、群、环、线性空间、拓扑空间之类的数学模型，构成它们世界的是数学对象，而不是那些呈现在日常生活中的东西。在这个意义上，它们是第二代数学模型。线性空间就是第二代模型的一个例子，它是通过公理化的方式来表述的，其构成元素也都是数学对象，不是生活对象，因此，学生理解起来较难。大部分学生只能非常具体地思考问题，碰到第二代模型的术语就感到困难。实际上，学生甚至在碰到最简单的与现实联系最紧密的模型时也会感到困难。

因此，在讲解这个线性空间概念时，我们可以引导学生们先设想一维线性空间（时间轴或数轴）、二维线性空间（平面上的向量集）、三维线性空间（立体空间上的向量集），然后进一步推广到多维线性空间，最终概括出其本质并给出定义——它是一个集合，在其中定义了两种运算加法与数乘，数是取自某个数域，且集合中的元素对加法与数乘具有封闭性，运算满足八条公理，这样一个集合就叫某个数域上的线性空间，或者把它看成一个代数结构。然后再给学生们找出一个多维线性空间的实例，如：齐次线性方程组AX=0的解的集合就是一个线性空间，我们试图通过具体的例子让学生们去进一步概括出、理解到这个概念。

矩阵的乘法，对学生来说是个难点。当讲到这里时，除了给出定义，还要说明并不是任意两个矩阵都能相乘，只有左边矩阵的列数等于右边矩阵的行数时乘法才能进行，这是由矩阵乘法的实质意义决定的。因此，我进一步讲了矩阵乘法的直观意义。给定数域P上m×n矩阵A和n×1矩阵X如下:

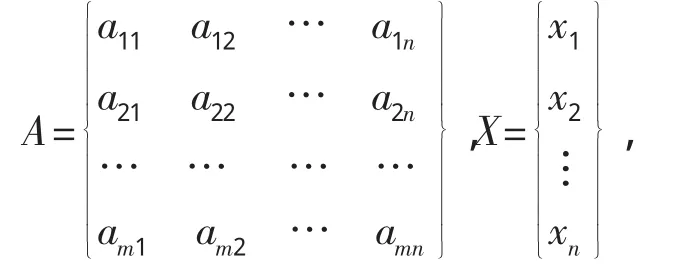
那么，按照矩阵乘法，

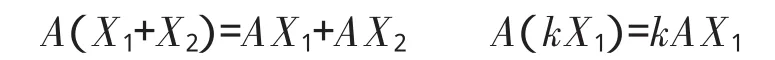
就是说，对于Pn中的两种运算：加法与数乘，在上述映射下对应于Pm内的加法与数乘，对运算具有保持性。本来Pn和Pm是数域P上的两个不同的线性空间，而矩阵乘法给出了它们之间保持加法、数乘对应关系的映射，等于在两者之间建立起了一座桥梁，使它们互相可以沟通。在二次型中应用的线性变换X=CY，C是可逆矩阵，其实也是映射这个含义。

当讲到矩阵的乘法不满足交换律时，也可以举例说明：一方面，交换后不一定可做乘法；即使能做，也不一定相等。可给出例题，直观认识，学生比较容易接受。

有时还可能要考虑好几个直观模型。然后在阅读证明或计算的过程时，把自己考虑的特例代入其中，并留心观察它的走向，发现一般的规律。

例如，求线性空间的一个向量在它的某个基下的坐标，我们可以先从一个具体的例题入手，寻找其一般的求解方法。

例 1 在线性空间 R3中，求向量 α=（1，2，1）关于基：α1=（1，1，1），α2=（1，1，-1），α3=（1，-1，-1）的坐标。解： 设向量 α 关于基 α1，α2，α3的坐标是（x1，x2，x3），则有3，即：

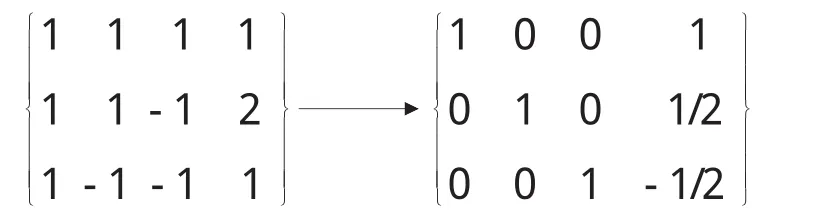
由此，推广到一般，我们可以发现这类问题的一般的求解方法。

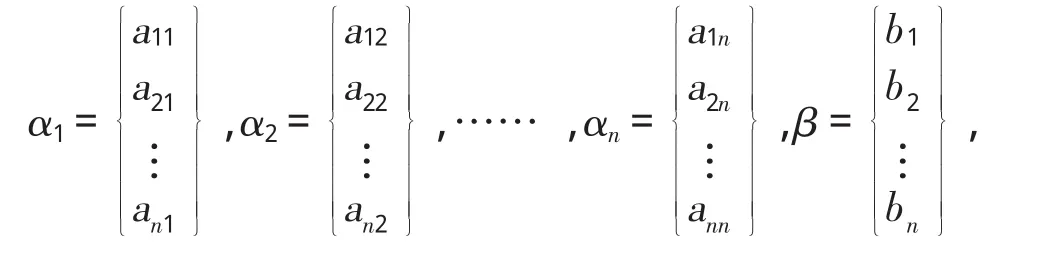
设在Pn中给定一组基和一个向量β：求向量 β 关于基 α1，α2，…αn下的坐标。实际上就是求解下列向量方程组的解：

把 α1，α2，…αn作为列向量排成一个 n 阶方阵 A，它就是上面线性方程组

的系数矩阵。因为A满秩，所以可单用初等行变换化为单位矩阵E，写出线性方程组的增广矩阵，用初等行变换把A化为E，则γ即为所求的坐标：

通过研究这些特例，就可以更深入地理解抽象理论的特点，从而接近问题的本质。教学中这些例题的穿插，会起到了直观的作用，直观的例题模型还可以在独立解决问题时起到导引思路的作用。

当开始思考一个复杂的问题时，可能会有若干种思路，如果把一些特例代入，很快就会发现有些思路根本走不通，于是就可以少走弯路。

选取一个好的直观模型是很重要的。一方面它不能太难，必须是已被自己掌握的；另一方面又忌太平凡，那样往往效力不够。通常一本书在介绍一个新概念后都会举出不少实例，这些是必须要留心掌握的。这种方法也有它的局限性，有不少数学概念就没有简单的例子加以说明。另外使用直观模型只是一种辅助手段，目的是帮助理解和提供思维的参考，它不能也不应该代替严格的推导过程。

3 趣味性教学

数学的抽象性，导致学生们学习起来感觉比较枯燥难学。因此如何将数学趣味化也是我常常思考的问题。教材往往是浓缩的精华，把它泡开，才能发现数学的趣味。这就需要我们去挖掘教材、拓展内容、与一些实际例子结合、与一些数学家生活工作的故事结合来激发学生学习兴趣，从而使数学教学更具趣味性。

例如：在讲解子空间的直和时，教材直接给出定义，然后是定理的证明，学生接受起来比较困难。而笔者在讲解时做了这样的处理：先讲解两个例题，一个是向量分解式不惟一的，一个是向量分解式惟一的。让学生们先直观感觉向量分解式的各种情况，产生兴趣，然后再引导到定义；再说明研究直和的目的，是为了在研究空间性质时把大的空间转换为子空间来进行。

另外，由于学生的毕业去向大多是小学，所以我还积极探索《高等代数》与小学数学教学的关系，寻找《高等代数》与小学数学教学之间的相关性。通过在教学中穿插一些与小学数学有关的内容，以提升教学内容的趣味性。比如，维数公式与小学数学集合题的联系。如果V1，V2是线性空间的两个子空间，那么，它们的维数关系有：

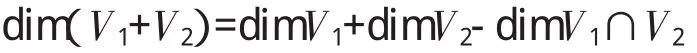
例2、 小学应用题：某班36人，参加数学、语文课外兴趣小组，每人至少参加一个小组，参加数学、语文的人数是20、28人，求同时参加两个小组的人数。解： 设同时参加两个小组的人数为x，

则 36=20+28-x，x=12。

后者在计算时与维数公式有内在的联系，本质上相同。

以上是我在教学中一些探讨。高等数学教学要求我们完成四个方面的任务：一是让学生认识与理解数学的内容；二是解决其枯燥感，揭示数学的趣味；三是介绍数学的应用，使学生觉得数学是具有实用价值的；四是培养学生的创新思维，要在动手做、动脑思考中学习，学会独立思考。因此，对教学的探索应该是多方面的，另外，我们也要注意培养学生的非智力因素，要求学生养成精细、严谨、简明的思维风格和不断设问的好奇心，以及通过数学的学习磨练学生坚忍不拔的毅力和刻苦钻研、不断创新的精神。

总之，教学是一门艺术，需要我们不断研究与探索，在数学的教学中更要求我们学会以直观克服数学的抽象性，以拓展揭示数学的趣味性。

［1］唐忠明.高等代数［M］.南京：南京大学出版社，2000.

［2］张禾瑞.高等代数第四版［M］.北京：高等教育出版社，1999.

［3］瑞典.L.戈丁.数学概观［M］.北京：科学出版社，2001.

［4］蓝以中.高等代数简明教程［M］.北京：北京大学出版社，2002.

［5］王庚.数学文化与数学教育［M］.北京：科学出版社，2005.

（责任编辑 赵巨涛）

O15

A

1673-2014（2010）05-0074-03

2010—09—13

黄国庆（1967— ），男，河南林州人，讲师，主要从事高等代数教学研究。