聚类分析在中等职业学校学生专业选择分析中的应用

2010-09-12王新龙

长治学院学报 2010年5期

关键词：中等职业数据挖掘聚类

王新龙

（长治学院计算机系，山西长治 046011）

聚类分析在中等职业学校学生专业选择分析中的应用

王新龙

（长治学院计算机系，山西长治 046011）

利用聚类分析能比较清晰的获得数据分布的情况，根据每一个簇的特点，可以对特定的簇作进一步分析。对中等职业学校学生入学成绩进行聚类分析是学生专业选择的重要参考。传统的专业选择方法存在一些不足，使用聚k-平均聚类分析算法对学生的入学成绩进行聚类分析，为学生提出专业选择的建议，可以有效地克服传统专业选择方法的不足。

聚类分析；k-平均算法；专业选择

中等职业学校主要招收十五、六岁的初中毕业生，学生年龄较小，多数家长和学生对专业要求了解不多或根本就不了解，往往有从众心理，出现盲目选报专业。而后期又会因专业学习困难，需要重新更换专业，造成学校资源及家庭时间、精力、资金的浪费，尤其是加重了贫困家庭的负担。我们经过调查、讨论认为，影响专业选择的主要因素有：学生的理科（数学、物理、化学）基础、文科（语文、政治、英语）基础、职业能力成绩、就业情况、个人爱好及性格特点等。通过对学生成绩的聚类分析，可以将学生群体按其成绩分为全面、偏理、偏文、一般等4类，以此聚类分析结果作为参考我们可以为学生专业选择提出比较合理的建议。

1 聚类技术的相关概念

数据挖掘可以简单的理解为从大量数据中提取或挖掘知识，许多人把数据挖掘视为数据库知识发现（KDD）。因此数据挖掘一般可表述为：从存放在数据库、数据仓库或其他信息库中的大量数据中挖掘有趣知识的过程[1]。

聚类分析仅根据在数据中发现的描述对象及其关系的信息，将数据对象分组。其目标是：组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内的相似性（同质性）越大，组间差别越大，聚类就越好。

聚类技术发展迅速，在数据挖掘、模式识别、机器学习、统计学、心理学、生物学、信息检索、空间数据库技术、市场营销等领域有着非常广泛的应用前景。由于数据库中收集了大量的数据，聚类分析已经成为数据挖掘研究领域一个非常活跃的研究课题。

2 聚类分析中的数据类型和数据结构

聚类分析主要针对的数据类型包括：区间标度变量（如：重量、高度、工资）；二元变量（如：0，1，或 Yes，No）；标称变量（如：traffic light具有红、黄、绿三种状态/停、看、行三种状态）；序数型变量（如：教授、副教授、讲师、助教；或者：总经理、部门经理、科长、职员）；以及由这些变量类型构成的复合类型。

一些基本的聚类算法通常采用数据矩阵和相异度矩阵两种典型的数据结构。

①数据矩阵：设有n个数据对象，可用p个属性来描述每个对象，则n×p矩阵称为数据矩阵。

②相异度矩阵：按n个数据对象两两间的相异度构建的n阶矩阵（因为相异度矩阵是对称的，只需写出上三角或下三角即可）称为相异度矩阵。

3 聚类分析的算法分类

目前存在大量的聚类算法，具体应用时应根据数据的类型和聚类的目的以及应用范围而选择相应的举法。到目前为止聚类的算法大体可分为如下几类：

①基于划分的方法。常见的算法有：k-平均算法，在该算法中每个簇用该簇中对象的平均值来表示；k-中心点算法，在该算法中，每个簇用接近聚类中心的一个对象来表示。

②基于层次的方法。常见的算法有：CURE、BIRCH和Chameleon等算法。

③基于密度的方法。常见的算法有：DBSCAN和OPTICS等算法。

④基于网格的方法。常见的算法有：WaveCluster和CLIQUE等算法。

⑤基于模型方法。常见的算法有：神经网络算法和COBWEB等算法。

4 k-平均算法

K-平均算法如下。

输入：蔟的数目个数k和包含n个对象的数据库；

输出：k个蔟，使平方误差准则最小；

方法：

（1）任意选择k个对象作为初始的簇中心；

（2）repeat；

（3）根据簇中对象的平均值，将每个对象（重新）赋给最类似的蔟；

（4）更新簇的平均值，即计算每个蔟中对象的平均值；

（5）until不再发生变化；

5 聚类分析在中等职业学校学生专业选择分析中的应用

中等职业学校主要培养学生既要具备一定的专业理论，更应该具有一定的职业技能水平，以适应社会的需求。但是每年大多数新生在专业选择上无章可循，不清楚自己应该学什么专业。例如：前几年计算机专业比较热，很多家长、学生也不考虑自己是否适合就要求上计算机专业，更不考虑市场需求量。现在进行毕业生跟踪调查并与其他专业作比较，我们会发现有不少学生认为当初的专业选择是错误的。

每年新生入学都要进行文化课和职业能力测试，如何科学地根据入学成绩和本人的实际情况给出学生比较适合的专业建议，是职业教育工作的首要问题。本文中主要使用了k-平均聚类分析算法来分析学生情况，从而给出专业建议及指导。

5.1 数据预处理

表1所示的是某职业学校09级100名学生的入学成绩（部分），为便于计算，考虑到多数专业对学生的数学、物理、化学基础要求较高，而对语文、政治、英语要求相对较弱，因此对数据进行如下处理：

理科成绩=（数学+理化）/2，文科成绩=（语文+政治+英语）/3；

均分=理科成绩×0.6+文科成绩×0.4，处理后的成绩见表2；

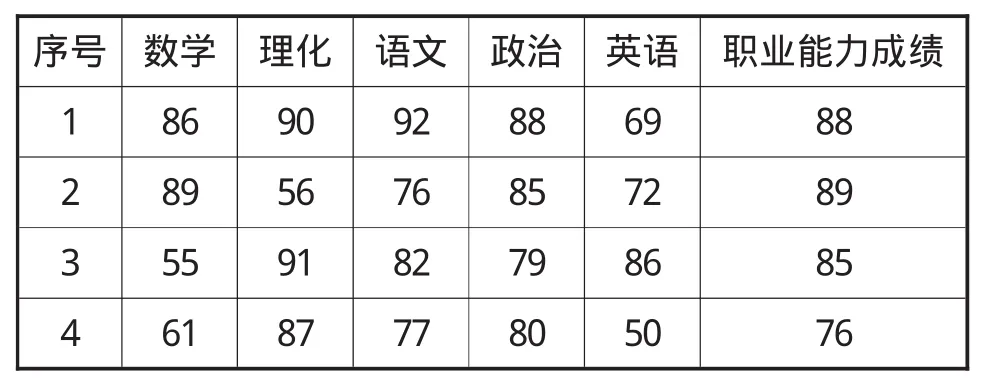
表1 某职业学校学生入学成绩表（部分）

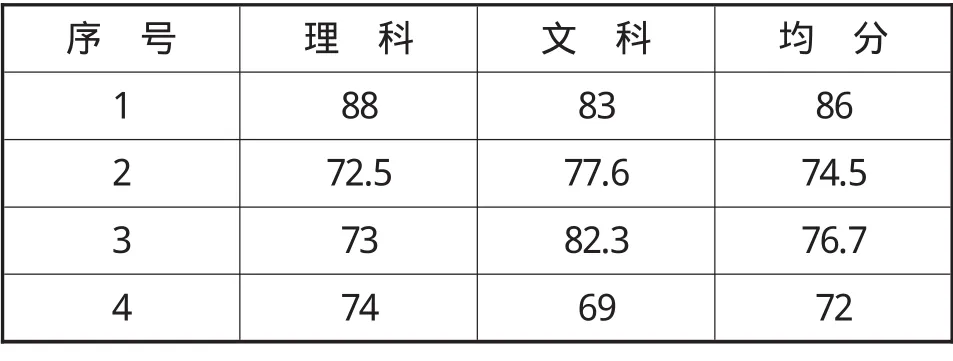
表2 经过数据处理的成绩表（部分）

职业能力成绩作为选报专业的参考成绩。

根据表2的均分成绩，按照k-平均聚类算法。若初始簇中心为 50、65、80、90，则划分的结果，如表3所示。

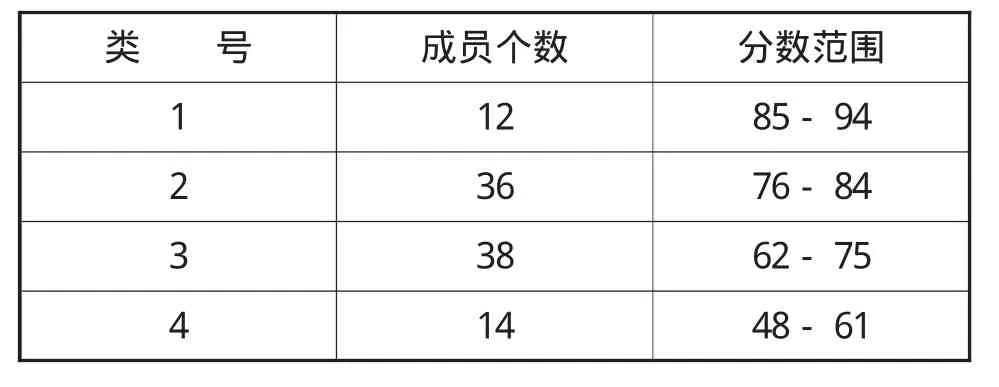
表3 k-平均算法分类结果

5.2 对上述结果进行解释

类1基本对应于学习成绩较好的一类学生，理科、文科、职业能力成绩都比较高，这类学生比较适合的专业比较多，如机械加工、电工、数控、物业管理、市场营销等。

类2基本对应理科成绩较好的学生，比较适合的专业为机械加工、电工、数控等专业。

因为这些专业对数学、物理基础要求较高，就业后有大量的故障分析和计算工作。

类3基本对应文科成绩较好的学生，比较适合的专业为：物业管理、旅游管理、文秘等专业。

类4基本对应各科成绩较差的学生，比较适合餐饮服务、市场营销、艺术类等专业或初级工种的学习。

这样在专业选择的时候，我们可以根据学生的成绩及个人特点，给学生提供较好的专业选择建议。

5.3 聚类分析结果与实际选报专业对比分析

通过对应用以上方法的09级100名学生实际专业选择情况调查，我们发现由于近年来数控加工技术工人短缺，就业形式较好，再加上媒体的报道宣传，这100名学生报数控加工专业的人数多达63人，与聚类分析结果有较大差别。经过这一年的学习，由于有数控编程、工程力学、加工工艺相关计算等课程难度较大，当初理科成绩较低现在还没有明显提高的少部分学生要求更换专业，给教学管理及正常教学工作的实施带来了一定的难度和资源的浪费。因此在未来的新生专业设置、选报专业指导等工作中，在充分做好市场调研的基础上，可以用聚类分析方法，结合学生兴趣、特点等给出比较科学的专业选择建议，帮助学生选择好专业。