一种将线性粘弹微分型本构方程应用到ABAQUS的方法

潘晓明,余俊,杨钊,孔娟

(1.同济大学岩土及地下工程教育部重点实验室,上海200092; 2.中南大学土木建筑学院,湖南长沙410075)

一种将线性粘弹微分型本构方程应用到ABAQUS的方法

潘晓明1,余俊2,杨钊1,孔娟1

(1.同济大学岩土及地下工程教育部重点实验室,上海200092; 2.中南大学土木建筑学院,湖南长沙410075)

以3参量Merchant模型、Poyning-Thomson模型,以及4参量Burger模型为例,推导3种常用微分型本构方程的松弛剪切模量Prony级数形式,并确定其在ABAQUS中的输入参数,供ABAQUS调用分析.以算例分析岩土流变性态,将3种模型的应变蠕变、松弛数值解与一维情形下的解析解进行对比,结果吻合较好.对土体采用Merchant粘弹性流变模型的过江盾构隧道进行粘弹性数值分析,得到管片位移均趋于稳定值,说明所提出的方法是正确和可靠的,可以应用于岩土工程数值计算.

微分型本构;Lap lace变换;Prony级数;蠕变;松弛;ABAQUS

对于岩土所呈现的各种不同的流变特性,一般采用3种方法进行描述.(1)通过室内或现场试验和实测[1-3],建立经验流变或蠕变公式;(2)建立积分型本构方程求解流变问题[4-6];(3)根据流变介质模型,建立微分型本构方程,对岩土体流变进行分析.第3种方法直观、形象,且便于有限元编程计算,因而得到广泛的应用[7-9].ABAQUS是目前国际上最为先进的大型通用有限元计算分析软件之一.它所提供的粘弹本构模型是基于松弛剪切模量Prony级数形式的积分型本构方程[10],这给传统岩土体线性粘弹微分型本构方程的应用带来了不便.本文研究一种将线性粘弹性微分型本构方程转化成松弛剪切模量的Prony级数形式的方法,以供ABAQUS调用分析.

1 线性粘弹微分型本构方程转换成Prony级数形式

岩土流变模型是以反映蠕变、应力松弛等为前提,利用弹性元件(胡克体)、粘性元件(牛顿体),通过串并联关系形成的各种流变模型.文中讨论的3参量Merchant模型、Poyning-Thom son模型,以及4参量Burger模型,分别如图1所示.

图1 流变模型Fig.1 Rheologicalmodel

1.1 微分型本构方程的Laplace变换[11-12]

线性粘弹性微分型本构关系可以表示为1.3 Merchant模型

M erchant模型的一维本构方程为

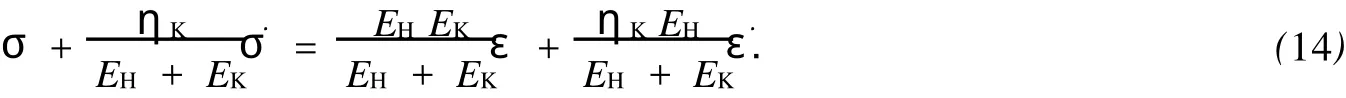
通过同样的方法,可得到Merchant模型在ABAQUS中的输入参数为

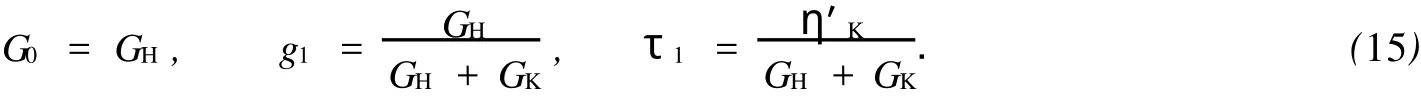
1.4 Poyn ing-Thom son模型

Poyning-Thom son模型的一维本构方程为

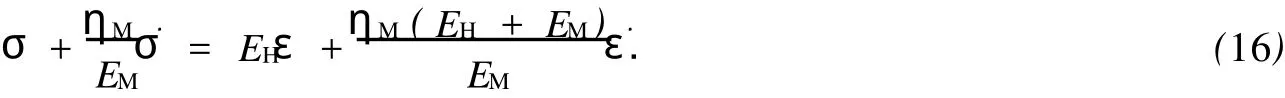
通过同样的方法,可得到Poyning-Thom son模型在ABAQUS中的输入参数为

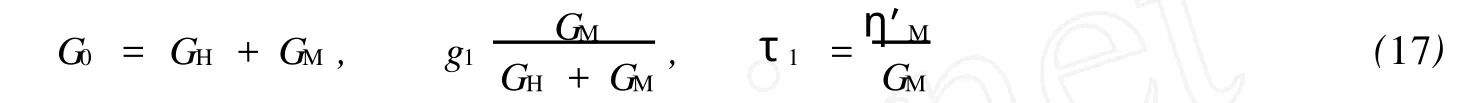
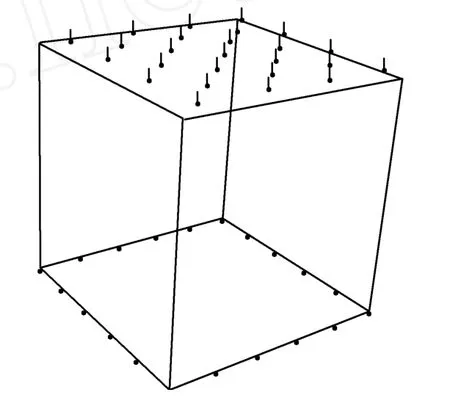
图2 三维计算模型Fig.2 Three-dimensional computationalmodel

2 算例验证

验证算例为一个三维C3D8单元试件,如图2所示.件长、宽、高均为1 m,试件底部固定,顶部受均布压力p进行蠕变试验数值模拟,以及施加恒定位移进行松弛试验数值模拟.材料基本参数:EH为2.0 M Pa,泊松比μ为0.25,EM为2.0 M Pa,ηM为21.6 M Pa·月,EK为2.0 M Pa,ηK为21.6 M Pa·月.

通过式(13)～(17),将微分型本构Burger模型、M erchant模型及Poyning-Thom son模型参数转换为可供ABAQUS调用的输入参数.

(1)Burger模型的一维蠕变和一维松弛解析解为

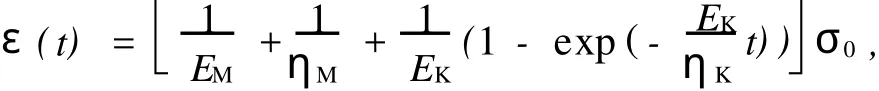
由此可以得到Burger模型在ABAQUS中的输入参数:E0=EM=2.0 M Pa,μ0=μM=0.25,g1= 0.768,g2=0.231,τ1=3.59,τ2=27.0.

(2)Merchant模型的一维蠕变和一维松弛解析解为

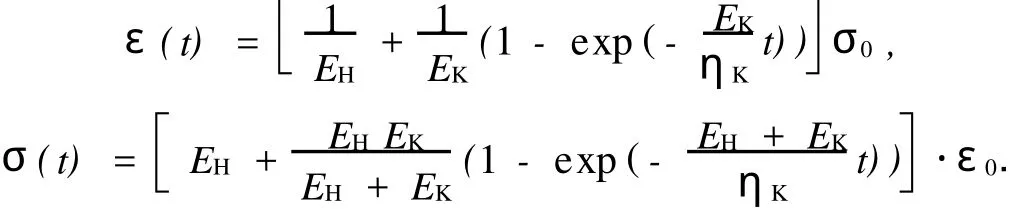
由此可以得到M erchant模型在ABAQUS中的输入参数:E0=EH=2.0 M Pa,μ0=μH=0.25,g1= 0.545 454 5,τ1=4.91.

(3)Poyning-Thom son模型的一维蠕变和一维松弛解析解为

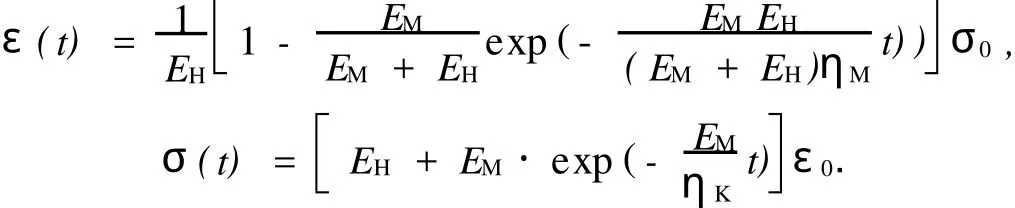
由此可得到Poyning-Thom son模型在ABAQUS中的输入参数,即E0=EH+EM=4.0 M Pa,μ0= μH=0.25,g1=0.454 545 45,τ1=10.8.

在ABAQUS中,应力以受压为负,受拉为正.在施加荷载的中,均布荷载p为0.1 M Pa,进行蠕变数值试验;恒定位移u3为0.3 m,进行松弛数值试验.

对于流变计算,在ABAQUS中一般设置两个分析步.第1个分析步为Static静力分析步,时间设置很小,如1×10-20s;第2个分析步为V isco准静态分析步,采用固定时间增量步为0.5月,计算总时间为150月.

在均布荷载作用下,Burger模型、Merchant模型及Poyning-Thom son模型的应变蠕变数值解与一维情形下蠕变解析解,如图3所示.从图3可知,Burger模型能够较好地模拟蠕变的第2阶段,其轴向应变ε随时间(t)的增加而增加;M erchant模型和Poyning-Thom son模型能够较好地模拟蠕变的第1阶段,轴向应变随时间的增加而趋于稳定值.

在常应变作用下,3种模型应力σ松弛数值解与一维松弛解析解,如图4所示.从图4可知,Buger模型存在应力松弛,随着时间的增加最终趋于零;Merchant模型和Poyning-Thom son模型具有松弛特性,随时间的增加最终趋于稳定值.

从图3,4可以看出,3种模型的蠕变及松弛的解析解与数值解吻合较好,蠕变最大相对误差不超过1.34%,松弛最大误差不超过1.28%.

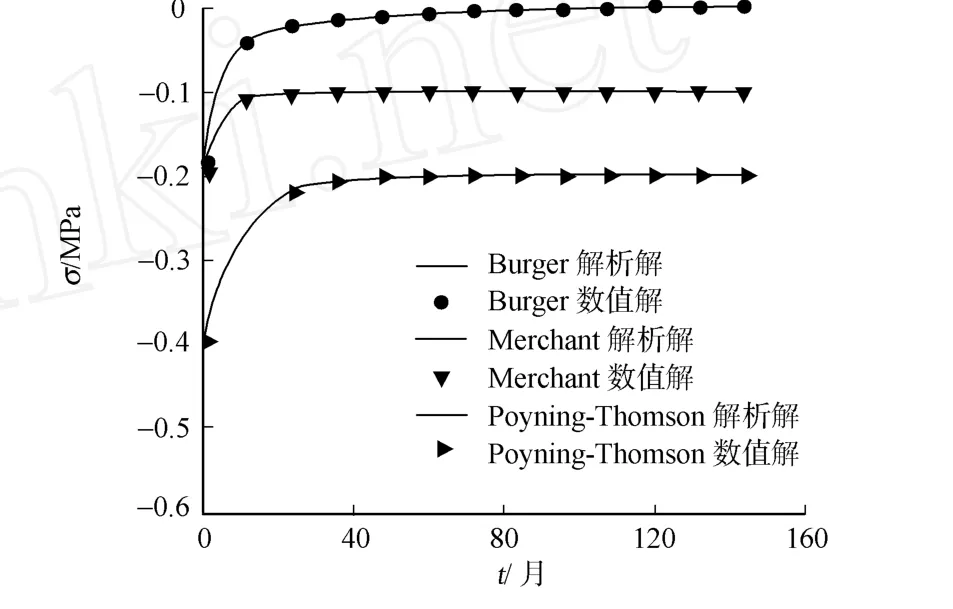
图4 模型轴向应力解析解与数值解比较 Fig.4 Comparison between analytical and numerical axial stresses

图3 模型轴向应变解析解与数值解比较Fig.3 Comparison between analytical and numerical axial strains

3 工程实例

某过江隧道衬砌外径外直径为8.7 m,管片内直径为7.9 m,管片厚为400 mm;有限元模型尺寸长60 m,宽79.38 m,拱顶埋深17.6 m,其网格图如图5所示.坐标系采用水平向右为X方向,垂直向上为Y方向.底部边界全约束边界条件,左、右侧边界则采用X轴方向对称约束,上部边界采用自由边界.

图5 有限元计算网格Fig.5 Finite elementmesh

土体单元选用双线性四边形完全积分单元,单元数5 275个,节点数5 525个.管片采用实体单元,选用能考虑弯曲并可克服剪切自锁的四边形双线性非协调等参单元.管片单元数168个,节点数252个.土体采用M erchant本构模型,试验参数和经转化为ABAQUS的粘弹输入参数,如表1所示.

隧洞中心处的外水压力为0.367 4 M Pa,拱顶至拱底的侧向水压力呈梯形分布.对砂性土采用水土分算,外水压力直接作用在管片衬砌外层周围.计算时设置4个分析步:(1)设置Geostatic重力分析步.计算后将土体位移场清零,只保留应力场;(2)设置为Static静力分析步.开挖隧道范围内土体并施加管片,计算时间为1× 10-20s;(3)设置为Visco准静态分析步.施加管片重力及外水压,计算时间为36月,时间增量为0.5月.

在第3个分析步开始时,管片在施加重力荷载及施加外水压作用下,瞬时产生的弹性变形如图6所示.从图6可知,由于管片接头位置不对称,造成水平位移不对称.在土体采用粘弹材料,计算时间为36月时,管片的位移云图如图7所示.从图7可知,管片水平相对位移由24.1 mm变化为17.8 mm;管片竖向相对位移由25.4 mm变化为19.5 mm.这主要是由于土体发生蠕变作用,使得管片有向内收敛.管片拱顶、拱底竖向位移,以及右侧拱腰水平位移随时间的变化曲线,如图8所示.从图8可看出,随着时间的增加,管片在不同位置处的位移均达到稳定的收敛值,这与一维情形下M erchant模型的蠕变特性相吻合.拱顶由瞬时弹性竖向位移-0.08 mm,经14月稳定至-16.2 mm;拱底竖向位移由25.3 mm变化至0.4 mm;右侧拱腰水平位移由13.5 mm变化至10.7 mm.

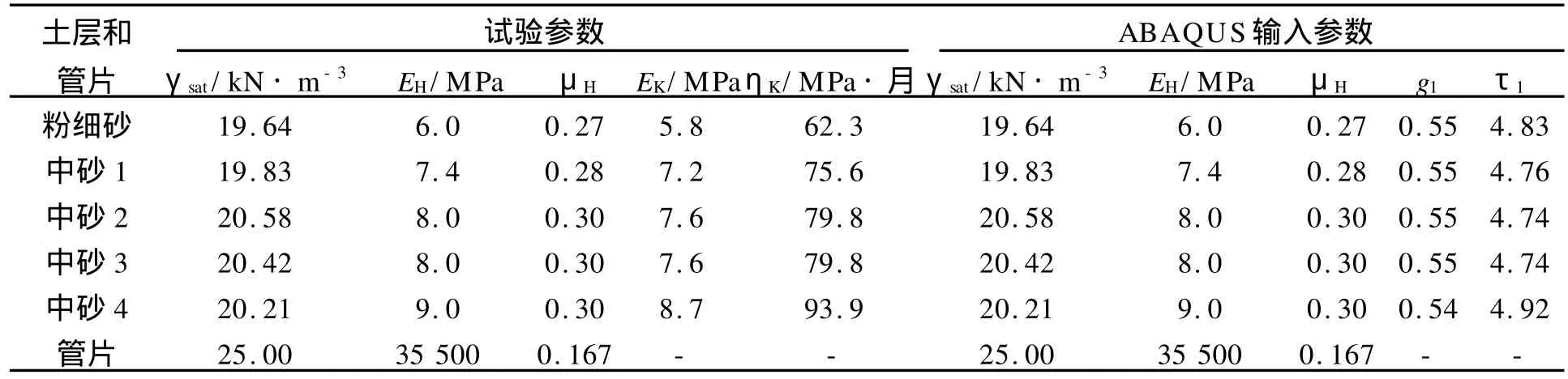
表1 土体计算参数表Tab.1 Computational parametersof soil

图6 Visco准静态分析步开始时的管片瞬时弹性位移Fig.6 Instantaneous elastic disp lacement of segment at the beginning of step 3

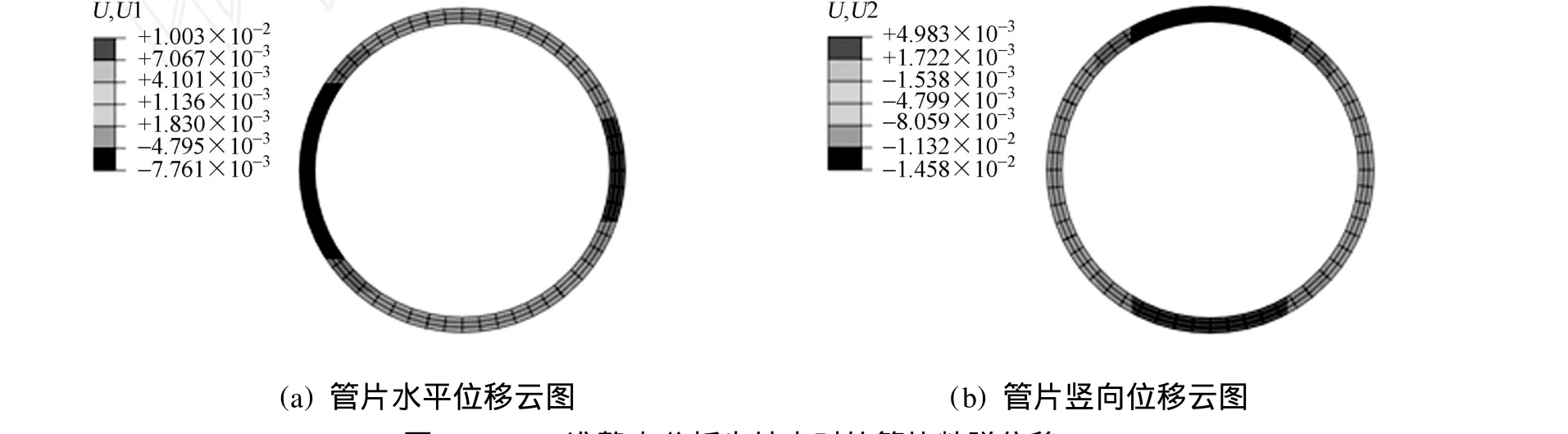
图7 Visco准静态分析步结束时的管片粘弹位移Fig.7 Visco-elastic disp lacement of segment at the end of step 3

4 结论

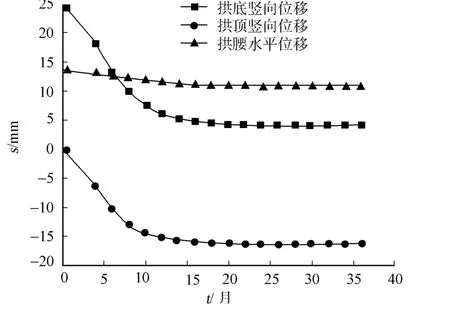
图8 管片位移随时间的变化曲线Fig.8 Curves of disp lacement to time at different location of segment

研究将线性粘弹微分型本构方程应用于ABAQUS分析平台的方法.推导Burger模型,Merchant模型及Poyning-Thom son线性粘弹微分型本构方程的松弛剪切模量p rony级数形式,并确定其在ABAQUS中的输入参数.

通过三维蠕变和松弛的数值模拟结果与一维情形下的解析解进行对比,表明两者的计算结果吻合较好.最后,对土体采用Merchant粘弹性流变模型的过江盾构隧道进行了粘弹性数值分析,得到了管片位移均趋于稳定值,进一步说明所提出的方法是正确的和可靠的,可以应用于岩土工程数值计算.

对于将其他线性粘弹微分型本构方程的应用到ABAQUS中,所提出方法具有一定的参考价值.

[1] 赵永辉.润扬长江大桥北锚碇土体流变特性的试验研究[J].地下空间,2003,23(4):417-420.

[2] 谢宁,孙钧.上海地区饱和软粘土流变特性[J].同济大学学报,1996,24(3):233-237.

[3] 刘朝丰,鲍文魁,徐景龙.剪切模量的近似函数和精确数值积分表达式[J].上海航天,2003,20(5):26-28.

[4] 焦春茂,赵春风,张征,等.遗传积分型本构方程的两种推演方法及比较[J].地下空间与工程学报,2008,3(4):42-45.

[5] 王琛,刘浩吾.线性积分模型和微分模型的普遍流变方程[J],土木工程学报,2003,36(10):99-102.

[6] THOMAS F S.Finite-element calculation of stresses in glass parts undergoing viscous relaxation[J].J Am Ceram Soc,1999,70(2):90-95.

[7] 孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999:1-40.

[8] 章根德,何鲜,朱维耀.岩石介质流变学[M].北京:科学出版社,1999:20-60.

[9] 王智祥,刘金明,刘柏雄,等.AZ61镁合金热压缩流变应力的实验[J].华侨大学学报:自然科学版,2009,30(3): 248-252

[10] HKS Inc.ABAQUS user’smanual[M].Paw tucket:Hibbit,Karlsson&Sorensen Inc,2002.

[11] 王芝银,李云鹏.岩体流变理论及其数值模拟[M].北京:科学出版社,2008:6-30.

[12] 陈子荫.围岩力学分析中的解析方法[M].北京:煤炭工业出版社,1994:303-390.

A Method Using L inear Viscoelastic D ifferen tial Constitutive Equation in to ABAQUS

PAN Xiao-m ing1,YU Jun2, YANG Zhao1,KONG Juan1
(1.Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education,Tongji University,Shanghai 200092,China; 2.School of Civil Engineering and A rchitecture,Central South University,Changsha 410075,China)

Taking three-parameter Merchantmodel,Poyning-Thomsonmodel and four-parameter Burgermodel as examp le,the relaxation shear modulus w ith p rony series fo rm s is derived by three kinds of commonly used differential-type constitutive equation,their parameters is determined to input in ABAQUS.In order to analyze the rheological characteristics,the creep and relaxation numerical solutionsof threemodelsagreewell to analytical solutions.Using Merchant viscoelastic rheologicalmodel,the viscoelasto numerical calculation of cross-river shield tunnel is carried out,the stabile values of segment displacement are obtained,w hich indicate the p roposed method is co rrect and reliable,and can be app lied to geotechnical engineering numerical calculation.

differential constitutive;Laplace transform;p rony series;creep;relax;ABAQUS

TU 452

A

(责任编辑:钱筠 英文审校:方德平)

1000-5013(2010)05-0570-06

2009-10-11

潘晓明(1979-),男,博士研究生,主要从事隧道及地下结构方面的研究.E-mail:p xm155138@163.com.

国家自然科学基金资助项目(40872179);中国博士后科研基金资助项目(20080440652)