中国股市跳跃行为的随机波动模型分析

高延巡,胡日东,苏梽芳

(华侨大学经济与金融学院,福建泉州362021)

中国股市跳跃行为的随机波动模型分析

高延巡,胡日东,苏梽芳

(华侨大学经济与金融学院,福建泉州362021)

基于上证综指样本数据,探讨双跳跃随机波动模型并研究股市波动跳跃行为.应用马尔科夫蒙特卡洛方法对模型参数进行估计,通过残差正态检验比较各类随机波动模型刻画股市波动能力,采用损失函数评价法和线性回归法,评估其对上证综指波动的预测精度.结果显示,中国股市跳跃波动程度和强度较大,对股市收益和波动均有显著影响;在引入跳跃成分刻画股市异常波动行为后,双跳跃模型显著提高股市收益波动率的估计精度与预测能力.

跳跃;杠杆效应;随机波动模型;马尔科夫蒙特卡洛方法;上证综指

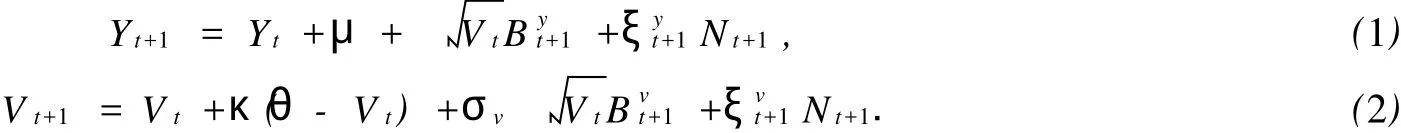
式(1),(2)中:Yt为t时刻资产的对数价格;Vt描述t时刻的即时波动率;参数μ度量资产的期望收益;θ描述波动率的长期均值;κ是波动率向长期均值修正的速率;σv衡量“波动的波动”;Byt+1与Bvt+1服从标准正态分布且corr(Bty+1,Btv+1)=ρ,当ρ<0时,波动存在杠杆效应,即资产价格的变化和波动之间的关系是非对称的,资产价格的下跌往往导致较大的波动;Nt+1是服从跳跃强度参数λ的泊松过程,表示在单位时间内跳动的次数.由于离散化的时间较短,Eraker等[4]假定单位时间间隔内(通常为1 d)只能发生一次跳跃,因此泊松过程实际上退化为贝努里分布;ξty+1与ξvt+1分别反映收益和波动发生跳跃的幅度,假定ξty

+1～N(μy,σ2y),ξvt+1～exp(μv),参数μy影响收益的偏度,当μy<0,则收益左偏;当σ2y较大时,则能更好地刻画收益尖峰肥尾的特性.此时,将EJP模型记为SV IJ模型,且记该模型的参数集为Θ= (μ,κ,θ,σv,ρ,λ,μv,μy,σy).

上述的EJP模型几乎涵盖国外学者提出的各类连续的随机波动模型,去掉波动方程中的跳跃成分,模型变为Bate[7]和Anderson等[8]研究的单跳跃随机波动模型(SVMJ模型).当不加入跳跃成分时,模型就退化为Heston[3]提出的非对称随机波动模型(ASV模型);当ASV模型的参数ρ=0时,模型为基本的随机波动模型(SV模型).

1.2 马尔科夫蒙特卡洛方法

从计量角度上看,无法直接得到EJP模型的似然函数,而且存在较多潜在状态变量Nt+1,故只能通过高维积分计算得到.为了克服这些困难,采用基于贝叶斯原理的马尔科夫蒙特卡洛(MCMC)模拟方法来估计模型的参数.其基本思想是:通过对模型参数的后验分布抽样构造一个平稳分布的马尔科夫链,然后基于此做出参数的各种统计推断.

下面仅给出EJP模型的似然函数,有

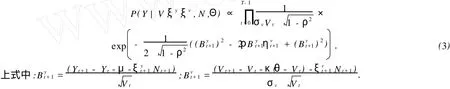
2 数据特征描述

采用2003年1月2日至2006年6月1日的5 min高频数据的上证综指为样本数据,共820个交易日(数据来源于中国经济研究中心的股票市场高频数据库),每个交易日有48个数据,即N=48,T= 820,共计39 360个.设Pt,0表示第t天的开盘价,Pt,48表示第t天的收盘价,定义日收益率为

同理,定义第t天每5 m in的高频数据收益率rt,n为

根据Anderson等定义[8],则第t天的5 m in高频数据的实现波动率RV为

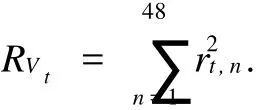
日收益平方及日收益的描述性统计,如表1所示.表1中:J-B值为Jarque-Bera统计量;Q(n)为滞后n期的L jung-Box的Q统计量;置信水平为1%;标准正态分布的偏度为0;峰度值也为0.

表1 日收益平方及日收益的描述性统计Tab.1 Square and daily return rate descrip tive statistics

由表1可知,日收益R有明显的正偏度和峰度,而日收益平方R2表现出强烈的尖峰肥尾的特性;两序列的正态分布统计量都很大,强烈拒绝正态分布的假定;同时,日收益平方序列存在明显的自相关性,说明中国股市波动存在显著的波动持续性特性.

3 随机波动类模型的实证结果比较分析

3.1 模型参数的估计

运用R 2.8.0软件,将上述样本数据分别对上述各类SV模型进行参数估计和统计推断并作比较分析,结果如表2所示.表2中括号中的数值为参数的标准差.

从表2可以看出,上述模型在刻画波动的杠杆效应后,期望收益μ一致为负,特别在描述跳跃后,期望收益更小.说明股市剔除杠杆效应及跳跃影响后,市场预期行情表现为下跌趋势.参数ρ表明波动率V与收益R之间存在较强的负相关关系,收益率下跌较大往往引起比等幅度的上涨有更大的波动;当发生跳跃后,波动率调整到较高的水平(θ)而波动的持续性降低(κ).跳跃强度参数λ反映中国股市每年大约发生7次(234×0.028)跳跃,远远大于欧美股市.表明,中国股票市场较不稳定,容易受到消息及政策等外在因素的影响,从而导致股市的大起大落.

表2 随机波动模型的MCMC参数估计结果Tab.2 Coefficients estimated resultsof stochastic volatility models by MCMC

3.2 残差的正态性检验

通过对残差的统计特征分析,来评价模型刻画股市的拟合能力.各类随机波动模型的残差统计分析结果,如表3所示.表3中:LM(12)是滞后12阶的ARCH效应检验,“[]”中数据为概率p值.

表3 随机波动模型的残差统计分析Tab.3 Statistical analysisof the residual erro rs of stochastic volatility models

如果模型的设定比较合理,那么其标准化的残差应该近似满足独立的标准正态分布,即

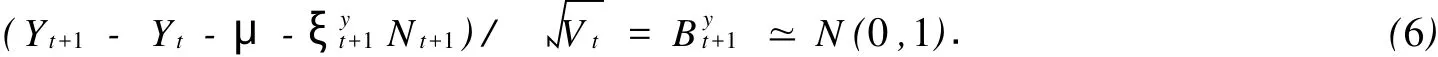
由表3可知,与日收益平方序列相比,各模型残差序列的偏度和峰度都有所降低,SVMJ模型和SV IJ模型较接近于标准正态分布.正态统计量J-B值表明,SV模型与ASV模型的残差序列强烈拒绝标准正态分布假定,说明SV模型与ASV模型的设定无法描述股市尖峰肥尾的特征,模型存在误设;而SVMJ模型与SV IJ模型较合理地刻画股市的波动特征.

标准化参数的独立性检验L jing-Box-Pierce统计量与ARCH效应统一表明,双跳跃SV IJ模型的标准化残差基本上满足正态分布与弱相关性假说,模型设定较为合理.

各类随机波动模型的标准化残差序列的分位数-分位数(QQ)图,如图1所示.图1中:QS,QT分别为样本分位数和标准正态分布分位数.从图1中可以证实,在加入跳跃项后,模型具有更高的拟合精度,能更好地捕捉股市异常波动行为.

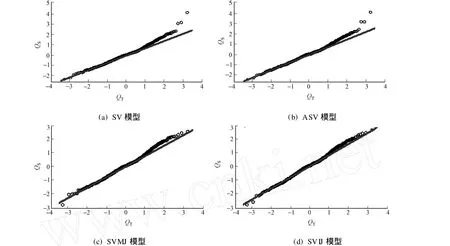
图1 随机波动模型的标准化残差序列QQ图Fig.1 QQ plotsof the standardized residualsof stochastic volatility models

3.3 预测精度的评价

评价各模型预测能力时,需要市场波动率的客观参考标准.Anderson等[8]研究表明,基于高频数据的实现波动率估计是真实市场波动率的一个较好的估计方法.以5 min的高频数据计算而得的实现波动率RV作为市场波动率的代理,来衡量各模型的预测精度.首先,根据Hansen的建议[3],采用平方平均误差EMS和平均绝对误差EMA两类损失函数进行评价.即

其次,采用实现波动率序列RV对事后波动率V进行回归.如果得到的判定系数R2值较高,说明该模型对波动率的预测能力较强.其构造方程为

各类模型预测能力评价比较结果,如表4所示.从表4的预测统计量EMA,EMS可知,具有跳跃成分的SVMJ与SV IJ模型预测效果优于ASV与SV模型,反映杠杆效应的ASV模型略优于基本的SV模型;线性回归方法表明,SVMJ模型的预测效果小于ASV与SV IJ模型.这是因为当收益发生巨大波动时,SVMJ模型的均值方程中的跳跃成分已经刻画了这一状况,而波动序列中仅仅包含平稳波动序列,所以,SVMJ模型的预测能力并不一定比ASV模型强.

表4 各类模型预测能力评价Tab.4 Predictive ability evaluation of stochastic volatility models

双跳跃SV IJ模型将平稳的波动序列与跳跃分开.当资产收益没有出现巨大波动时,模型与SVMJ模型一样能描述平稳波动序列;当出现跳跃现象时,波动率从Vt瞬时增加到Vt+ξvt,及时捕捉股市巨大波动行为.SVMJ模型与SV IJ模型波动跳跃图,如图2所示.图2中:T为研究数据段股市总共交易的天数;R为日收益率;RJ为跳跃收益率的跳跃大小;V为波动序列;VJ为波动的跳跃大小.

从图2可知,跳跃对收益和波动具有较大影响,SV IJ模型的波动序列相对小于SVMJ估计的序列,证实了估计出来的波动序列不含有跳跃成分,因此较好预测波动率未来的波动状况,两种评价方法都证实双跳跃SV IJ模型具有较强的预测能力.

图2 SVMJ模型与SV IJ模型波动跳跃图Fig.2 Volatility and jump p lo ts of SVMJ and SV IJ models

4 中国股市跳跃特征分析

与欧美国家相比,中国股市起步较晚,市场不规范,股票市场易受政策或消息等外界因素的影响,股市经常出现较大波动.因此,跳跃现象成为中国股市的一个重要特征.通过对上证综指的实证研究及图2说明,当国家出台相关政策或出现非典等外在因素时,收益出现较大波动,跳跃明显,规模较大.

2003年1月6日,超级大盘股中国联通、招商银行、中国石化等同时在历史最低价启动,引发行情的激烈波动;2003年4月,“非典”流行,股市行情出现跌落;2004年2月2日,《国务院关于推进资本市场改革开放和稳定发展的若干意见》出台,股指跃过2003年的1 650点高点继续上行;2004年8月31日,大盘震荡下探迫近1 300点,证监会发布通知暂停发行新股,IPO定价制度酝酿重大变更,将推广首发询价制度,大盘当日涨1.72%;2005年1月24日,印花税当日起由千分之二下调为千分之一,大盘涨1.73%;2005年5月9日,股权分置改造试点正式启动,上证指数当日再创新低,大跌2.44%;2005年6月6日,证监会推出《上市公司回购社会公众股份管理办法(试行)》,股指跌破千点;2005年9月5日,《上市公司股权分置改革管理办法》正式出台,大盘由998反弹至1223点后回落筑底;2006年5月8日,“五一”长假后首个交易日,上证指数大涨3.95%.

另外,当股市出现正跳跃之后往往出现负跳跃,说明中国股市的投机成分较大,缺乏理性的长期资本投资.即每当出现利好消息时,市场表现为非理性疯涨,之后便陷入低迷状态.

5 结论

运用各类SV模型对中国股市的跳跃行为等特征进行实证研究,结果表明,杠杆效应与跳跃是中国股市的重要特征.引入杠杆效应与跳跃成分的双跳跃SV IJ模型,在对波动率的拟合精度、刻画股市的动态行为特征的表现,以及对股市波动率的预测能力等方面都显著提高.

中国股市容易受到消息及政策等外在因素的影响,跳跃强度远大于欧美的股市.中国股市投机成分较大,缺乏理性的长期资本投资,当股市出现利好的正跳跃波动之后往往出现负跳跃波动;而在双跳跃SV IJ模型中引入跳跃成分之后,跳跃成分解释了股市的巨大波动行为.

[1] 周彦,张世英,张彤.跳跃连续时间SV模型建模及实证研究[J].系统管理学报,2007,16(5):531-536.

[2] DUFFIED,PAN J,SINGLETON K J.Transform analysis and asset p ricing for affine jump-diffusions[J].Econometrica,2000,68(6):1343-1376.

[3] HESTON S.A closed-fo rm solution fo r op tionsw ith stochastic volatility w ith app lications to bond and currency options[J].Review of Financial Studies,1993,6(2):327-343.

[4] ERA KER B,JOHANNESM,POLSON N.The impact of jumps in volatility and returns[J].Journal of Finance, 2003,58(3):1269-1300.

[5] 陈浪南,童汉飞,洪如明,等.波动率研究[M].北京:中国财政经济出版社,2008:183-219.

[6] 王春峰,姚宁,房振明,等.中国股市已实现波动率的跳跃行为研究[J].系统工程,2008,26(2):1-6.

[7] BA TESD.Jumps and stochastic volatility:Exchange rate p rocesses imp licit in deutschemark op tions[J].Review of Financial Studies,1996,9(1):69-107.

[8] ANDERSON T G,BOLLERSLEV T.Answering the skep tics:Yes,standard volatility models do p rovide accurate fo recasts[J].International Economic Review,1998,39(4):885-905.

Analysis of the Stochastic Volatility M odelsabout the Jump Behavior in Chinese Stock Market

GAO Yan-xun,HU Ri-dong,SU Zhi-fang
(College of Econom ics and Finance,Huaqiao University,Quanzhou 362021,China)

On the basis of Shanghai composite index,the double-jump stochastic volatility model and the jump behavio r of stock market have been discussed in this paper.Estimating the models through Markov Chain Monte Carlo methods, comparing the stock market volatility in the stochastic models by the no rmal residual test and evaluating p rediction p recision of the Shanghai composite index volatility by using the loss function method and the linear regression method,we get a resultw hich show s that thewaving range and jumping intensity in Chinese stock market are larger,w hich greatly affects on income and wave of the stock market;that the double-jump stochastic volatility model obviously imp roves the estimation p recision and the p rediction ability after introducing the jump into describing the abnormal volatility.

jump;leverage effect;stochastic volatility model;Markov Chain Monte Carlo methods;Shanghai composite index

O 211.67;F 830.91

A

1 随机波动模型的建模分析

EJP模型来研究上证综指的收益波动行为,有

(责任编辑:陈志贤 英文审校:司福成)

1000-5013(2010)05-0580-06

2009-11-27

胡日东(1964-),男,教授,主要从事金融工程与金融管理的研究.E-mail:j_rdhu@hqu.edu.cn.

国家社会科学基金资助项目(08BJL 019);华侨大学科研基金资助项目(09BS502)

作为市场风险的度量,对波动率的有效辨识是资产配置与投资策略、金融衍生品定价的前提,也是金融机构日常风险管理的基础.准确、有效地估计和预报波动率,一直是金融学家所探讨的热点问题.传统理论认为,金融资产(股票或外汇)的交易价格具有“时间连续性”,因此金融资产收益是稳定的.但是,最近有许多学者发现,金融市场经常受到外在因素(如重要消息或突发事件)的冲击,资产收益率就会在短时间内出现大幅波动,即所谓的“跳跃”现象.当市场存在跳跃现象时,自回归条件异方差(ARCH)类模型估计的波动序列是不稳定的,而随机波动(SV)类模型时变方差遵循某种不可观测的随机过程,通过加入跳跃成分,能有效地估计波动率.目前,国内学者对金融资产收益率的研究大部分局限于尖峰肥尾、长记忆性及杠杆效应特征分析,较少涉及到资产收益的跳跃行为及其对波动率影响的实证研究.周彦等[1]采用具有跳跃连续时间随机波动模型对不同时期中国股市波动跳跃分析,得出近期跳跃强度有所减弱.Duffie等[2]在Heston[3]提出的基本随机波动模型的基础上,提出一类跳跃的波动模型(AJD模型),认为收益的跳跃行为及其呈现的聚群现象影响波动率,并且这种反馈效应影响到资产收益的未来趋势.Eraker等[4]在此基础上进行相应调整得到EJP模型,并研究美国股市,则显著提高收益的拟合能力.陈浪南等[5]运用EARIV-GARCH模型对沪深股指数研究,得出B股指数跳跃概率高于A股指数.王春峰等[6]应用HAR-RV-CJ模型对上证综指实现波动率预测,得出离散跳跃方差不影响实现波动率预测.本文对双跳跃随机波动模型与其他随机波动模型进行比较,并评价各类模型在刻画金融资产的拟合与预测能力.

1.1 随机波动模型