单叶调和函数及其反函数为调和拟共形的充要条件

胡春英,黄心中

(华侨大学数学科学学院,福建泉州362021)

单叶调和函数及其反函数为调和拟共形的充要条件

胡春英,黄心中

(华侨大学数学科学学院,福建泉州362021)

研究平面上具有形式f(z)=A[αz+β+log(1-exp(-αz-β))-log(1-exp(-αz-β))]+B的保向单叶调和映照,其中A,B,α,β是常数且满足条件A≠0,α≠0.给出了定义在椭圆和上半平面上的单叶调和函数及其反函数都是调和拟共形映照的充要条件,并推广到一般的单连通区域上.

单叶调和函数;拟共形映照;复特征;调和拟共形映照

1 预备知识

一个复值函数f(z)=u+i v在平面区域D上调和是指u,v在区域D上实调和.如果D是一个单连通区域,则f可写为f(z)=h(z)+g(z),其中h,g为解析函数.Lew y[1]给出了f局部单叶且保向的充要条件为Jf=|h′|2-|g′|2>0,z∈D.文[2]证明了如下定理.

定理A 假设f(z)=h(z)+g(z)是一个单连通区域D上的保向单叶调和映照,则其反函数z= f-1(w)在G=f(D)内调和当且仅当下列3种情形之一成立:(Ⅰ)f(z)在D内共形;(Ⅱ)f(z)是仿射变换,即f(z)=αz+β¯z+B,|α|>|β|>0;(Ⅲ)f(z)具有形式为

式(1)中:A,B,α,β是常数且满足条件Re(αz+β)>0,z∈D.

单叶调和函数何时为单叶调和拟共形映照是一个研究热点.Pavlovic′[3-4]研究了单位圆和上半平面上的单叶调和函数为拟共形映照的条件,文[5]中也给出了单位圆到自身上的调和同胚为调和拟共形同胚的条件.本文研究单叶调和映照及其反函数都是调和拟共形映照的条件.定理A的结果表明,只需对具有形式(1)的情形加以研究.

2 主要结果和证明

3 一般区域上的情形

定理3 设D为有界单连通开区域,其边界为∂D∶φ(x,y)=0,且φ∈C1.f是定义在D上的保向单叶调和映照,且具有式(1)的形式,则f的反函数是调和拟共形映照的充要条件,存在一个实常数c> 0,使得对任何满足方程

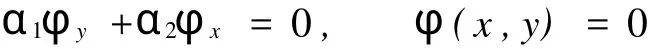
的z＊,有Re(αz＊+β)≥c.

证明 因D为有界单连通开区域,则￣D为有界单连通闭区域,所以Re(αz+β)必在边界∂D上取到最小值.由拉格朗日乘数法,设

又因为满足方程组(9)的点z＊∈∂D,所以有Re(αz＊+β)≥c.

当D为无界单连通开区域时,类似于定理3的证明可得到如下定理.

定理4 设D为无界单连通开区域,其边界为∂D∶φ(x,y)=0,且φ∈C1.f是定义在D上的保向单叶调和映照,且具有式(1)的形式,则f的反函数是调和拟共形映照的充要条件,存在一个实常数c> 0,使得α,β满足以下两个条件.

(1)对任何满足方程

又因为满足方程组(9)的点z＊∈∂D,所以有Re(αz＊+β)≥c.在上述4个定理中,若令c=0,则可得到函数f及其反函数都是调和映照的充要条件.

[1] LEW Y H.On the non-vanishing of the Jacobian in certain one-to-onemappings[J].Bull Amer Math Soc,1936,42 (10):689-692.

[2] 张兆功,刘礼泉.单叶调和映照的反函数[J].数学进展,1996,25(3):270-276.

[3] PAVLOV IC′M.Boundary co rrespondence under harmonic quasiconfo rmal homeomo rphisms of the unit disk[J]. Ann Acad Sci Fenn Math,2002,27(2):365-372.

[4] KALAJD,Pavlovic′M.Boundary co rrespondence under quasiconfo rmal harmonic diffeomo rphisms of a half-p lane [J].Ann Acad Sci Fenn Math,2005,30(1):159-165.

[5] 黄心中.单位圆盘上的调和拟共形同胚[J].数学年刊:A辑,2008,29(4):519-524.

Necessary and Sufficien t Condition that Un ivalen t Harmon ic Functionsand Their Inverse Functions are Harmon ic Quasiconformal Mappings

HU Chun-ying,HUANG Xin-zhong
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

Plannar sense-p reserving univalent harmonic functions w ith the form f(z)=A[αz+β+log(1-exp(-αzβ))-log(1-exp(-αz-β))]+B,are considered,w here A,B,α,βare constantsw ith the condition A≠0,α≠0.Necessary and sufficient condition fo r such harmonic functions defined ellip tic domain or on the upper half p lane and their inverse functions to be harmonic quasiconformalmappingsareobtained.Ourmethodsalso can be app lied to the general simp ly connect domains.

univalent harmonic functions;quasiconformalmappings;comp lex dilatation;harmonic quasiconfo rmal mappings

O 174.51

A

(责任编辑:陈志贤 英文审校:张金顺,黄心中)

1000-5013(2010)05-0586-04

2009-05-21

胡春英(1979-),男,讲师,主要从事函数论的研究.E-mail:huchunying@sina.com.

福建省自然科学基金资助项目(2008J0195);华侨大学科研基金资助项目(09HZR23)