无衍射光束最大准直距离的几何光学模拟与实验

郑维涛,吴逢铁,卢文和,张前安

(华侨大学信息科学与工程学院,福建泉州362021)

无衍射光束最大准直距离的几何光学模拟与实验

郑维涛,吴逢铁,卢文和,张前安

(华侨大学信息科学与工程学院,福建泉州362021)

利用几何光学方法对轴棱锥产生近似无衍射光进行分析,给出最大无衍射距离的几何表达式.利用光学设计软件ZEMAX对产生近似无衍射光的光路进行追迹,并模拟横向光强分布.通过几何分析、软件模拟及实验验证,讨论光束半径和轴棱锥底角对最大无衍射距离的影响.研究结果表明,最大无衍射距离随入射光束半径的增大而增大,且近似成正比;而最大无衍射距离随轴棱锥底角增大而减小,且近似成反比.

近似无衍射光束;轴棱锥;最大无衍射距离;ZEMAX软件

无衍射光具有的主光斑尺寸小(约为微米量级)、强度高、方向性好、准直距离较长等特点[1],人们对它的特性和应用进行了多方面的研究[2-10].在无衍射光的这些应用中,很大一部分(如光学精密准直、小物体测量、测距、带电粒子加速等)都取决于无衍射光束的准直距离,即最大无衍射距离Zmax.在最大无衍射距离内,光束能量和尺寸基本保持不变,但是超过这个距离,光能量迅速衰减为零.所以,最大无衍射距离是衡量无衍射光束的一个十分重要的参量.之前,人们已经利用衍射理论对无衍射光的最大准直距离进行了描述[11].光学设计软件ZEMAX是一个用来模拟、分析和辅助设计光学系统的软件.最近,文[12]利用光学设计软件ZEMAX对无衍射光的自再现进行了模拟,形象地追迹了近似无衍射光的重建过程.本文运用光学设计软件ZEM AX,对轴棱锥产生的近似无衍射光的最大无衍射距离的影响因素进行分析,同时对影响无衍射光束最大无衍射距离的因素进行了探讨.

1 最大无衍射距离的几何分析

目前,已有多种方法能够在有限孔径下实现近似无衍射光,如环缝-透镜法、谐振腔法、计算机全息法、轴棱锥法、球差透镜法,等等.其中,最常用也最简单的方法是线性轴棱锥法.它对能量的利用率高,结构简单[13],只需要单一元件就可以产生无衍射光束,并且所产生的无衍射光束尺寸稳定性好.

图1 轴棱锥产生无衍射光的光路Fig.1 Geometrical scheme of non-diffraction beam s generated by an axicon

当一列平面波入射到光学性质不同的两个媒质的界面上时,满足折射定律.设轴棱锥介质折射率为n,轴棱锥的棱角为γ,波矢k与z轴的夹角为θ,如图1所示.根据光的折射定律可以得到

式中:γ,θ及γ+θ的值均在10°以内.由小角度近似可得sinγ=γ,sin(θ+γ)=θ+γ,由此可得θ=(n-1)γ.

设入射到轴棱锥面的光束半径为R,则平行光通过轴棱锥后产生的近似无衍射光束的最大准直距离的近似解为

由式(2)可知,在入射光波长确定的情况下,轴棱锥产生的近似无衍射光束的最大无衍射距离仅与入射光束半径和轴棱锥底角有关.

2 光学设计软件ZEMAX模拟

2.1 光束半径对最大无衍射距离的影响

利用光学设计软件ZEMAX,可以直观地模拟光线通过轴棱锥后的光路,从而更好的进行分析.用ZEMAX软件对轴棱锥产生的近似无衍射光进行纵向模拟,如图2所示.横向光强分布的模拟图和实验拍摄图,如图3所示.

在选取模拟参数时,取λ=633.27 nm的红光作为光源,轴棱锥的材质设置为石英晶体,其折射率n为1.458,底角γ为2°.分别对不同入射光束半径R进行模拟,其二维输出如图4所示.由图4可知,最大无衍射距离随入射光斑半径R的增大而增大,并且近似成正比.

图4 不同入射光斑半径的几何光线追迹图Fig.4 Geometrical ray-tracing for different incident beam spot

图5 不同轴棱锥底角的几何光线追迹图Fig.5 Geometrical ray-tracing for different base angle of axicon

图2 轴棱锥产生无衍射光的几何光线追迹Fig.2 Geometrical ray-tracing of non-diffraction beams generated by an axicon

图3 横向光强分布Fig.3 Transverse intensity distribution

2.2 轴棱锥底角对最大无衍射距离的影响

同样,仍然取λ=633.27 nm的红光作为光源,轴棱锥的材质为石英(n=1.458).此时,固定入射光斑直径R为15 mm,分别对不同轴棱锥底角γ进行模拟,得到的二维输出如图5所示.由图5可见,最大无衍射距离随轴棱锥底角增大而减小,并且近似成反比.

3 实验结果及分析

通过相关实验验证以上分析,实验装置示意图如图6所示.在实验中,使用He-Ne激光器作为光源,其发射波长为633.27 nm,最大输出功率为3 m V,准直透镜的焦距f1=35 mm,f2=175 mm,两个透镜的焦点相互重合,组成准直系统.经过准直系统的平行光线射入轴棱锥,之后产生近似无衍射贝塞尔光.

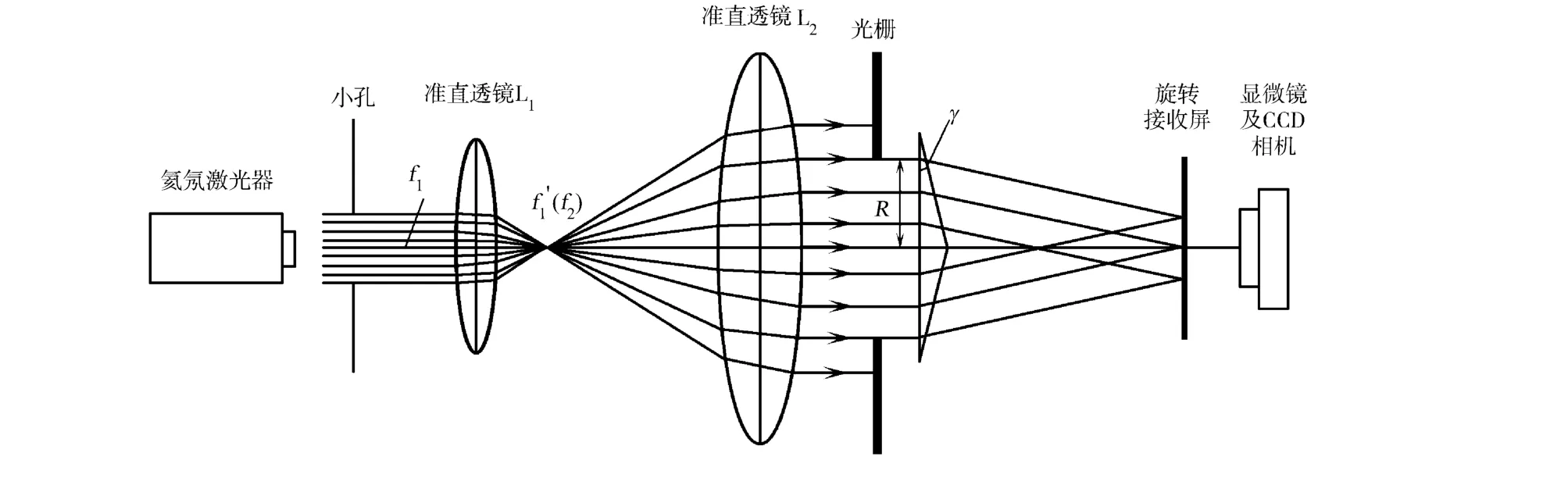
图6 实验装置示意图Fig.6 Diagram of the experimental setup

利用体视显微镜(最大可连续放大倍数为50倍)和CCD照相机(最大可连续放大倍数为5倍)组成的系统,可以拍摄到旋转接收屏上接收到的光斑图样.通过改变光阑孔径的大小及使用不同的轴棱锥,可以得到不同的最大无衍射距离.经过分析,可以得到入射光束半径和轴棱锥底角与无衍射光束最大无衍射距离之间的关系.

将实验所得最大准直距离Zmax结果与利用几何光学计算得到的结果,以及用光学软件ZEMAX模拟得到的结果进行比较,如表1所示.

表1 最大准直距离的结果比较Tab.1 Comparison of differentmaximum non-diffracting distance mm

通过表1可以看到,轴棱锥底角确定,也就是使用同一个轴棱锥时,无衍射光束的最大无衍射距离会随光阑半径的增大而增大,几乎呈正比例函数.当固定光阑半径时,无衍射光束的最大无衍射距离会随轴棱锥底角的增大而减小,几乎呈反比例函数.无论是用几何光学计算,还是用ZEMAX模拟,或者是用实验测量,都可以得到以上结论,这与式(2)十分吻合.

从表1还可知,几何光学计算值与ZEMAX模拟值十分接近,误差很小,而实验测量值与前两者之间则有一定的误差.引起这些误差的原因可能有如下两个方面.

(1)由于轴棱锥的底角很小(分别为2°和6°),这样高的精确度在加工过程中是相当困难的.由式(2)可知,γ角的误差将直接引起最大无衍射距离的误差.

(2)在实验中,确定旋转屏是否处于最大无衍射距离处,是通过肉眼观察CCD相机上接收到的光斑图样来确定的,这样也会引起测量误差.

4 结束语

通过对轴棱锥产生的近似无衍射光束的最大无衍射距离的软件模拟和实验验证,得到了近似无衍射光最大无衍射距离与入射光半径和轴棱锥底角之间的关系.即最大无衍射距离与入射光半径近似成正比,而与轴棱锥底角近似成反比.这与几何光学分析是相吻合的.用传统的衍射理论分析方法能够很精确的分析光束的传输,而用ZEMAX软件进行分析,最大的优点就在于它可以直观地显示光路.

[1] 吕百达.贝塞耳光束的特性和无衍射光束相关概念的分析[J].量子电子学,1996,13(2):97-104.

[2] L IN Y,SELA W,HEBERL Y J,et al.Experimental investigation of Bessel beam characteristics[J].App l Op t,1992,31(15):2708-2713.

[3] COX A J,DANNA J.Constant-axial-intensity nondiffracting beam[J].Op t Lett,1992,17(4):232-234.

[4] LOHMANN A W,OJEDA-CASTANEDA J,SERRASO-HERED IA A.Bessel functions:Parallel disp lay and p rocessing[J].Op t Lett,1994,19(1):55.

[5] MANZ T,SCHWARZ U T.Max maier stimulated stokes and anti-stokes raman scattering in liquid acetone w ith a Bessel beam[J].Op tics Communications,2004,235(1/2/3):201-217.

[6] GARCES-CHAVEZ V,MCGLO IN D,M ELV ILLE H,et al.Simultaneous micromanipulation in multiple p lanes using a self-reconstructing light beam[J].Nature,2002,419(6903):145-147.

[7] LEIM ing,YAO Bao-li.Characteristics of beam p rofile of Gaussian beam passing through an axicon[J].Op t Commun,2004,239(4/5/6):367-372.

[8] JUN A,KAZU TO Y,DA ISU KE S,et al.Laser-based microp rocesses using diffraction-free beams generated by diffractive axicon[J].Pro of SPIE,2005,5713:497-507.

[9] 蒋志平,陆启生,刘泽金,等.贝塞尔光束的应用[J].光学技术,1997(1):2-6.

[10] 刘岚,吴逢铁,曾夏辉.无衍射光束的轴上光强和最大准直距离[J].华侨大学学报:自然科学版,2007,28(4):350-352.

[11] 刘彬,吴逢铁,邱振兴.衍射和干涉理论对Bessel光束传输的描述[J].强激光与离子束,2007,19(12):1992-1996.

[12] 吴逢铁,江新光,刘彬,等轴棱锥产生无衍射光束自再现特性的几何光学分析[J].物理学报,2009,58(5):3125-3129.

[13] 吴逢铁,曾夏辉.相干贝塞尔光产生具有塔尔博特效应的局域空心光束[J].光学学报,2008,28(1):174-178.

Geometrical Optical Simulation and Experiment of Maximum Collimation Distance for an Non-Diffracting Beams

ZHENGWei-tao,WU Feng-tie, LU Wen-he,ZHANG Qian-an
(College of Info rmation Science and Engineering,Huaqiao University,Quanzhou 362021,China)

In this paper,non-diffracting beam generated by the axicon was analyzed using geometricalop ticalmethod and the exp ression of the maximum non-diffracting distance was given.The non-diffracting beam was traced using the op tical design software ZEMAX,and the transverseop tical intensity distribution was also simulated.The effectof the beam radius and the base angleγof the axicon on themaximum non-diffracting distance were discussed through the geometric analysis,software simulation and experiment.Results show that themaximum non-diffracting distance increasesw ith the increasing of beam radius R,and almost p ropo rtional w ith the R;however themaximum non-diffracting distance decreases w ith the increasing of the base angleγof the axicon,and inverse p roportional w ith theγ.

app roximate non-diffraction beam s;axicon;maximum non-diff racting distance;ZEMAX software

O 436

A

(责任编辑:黄仲一 英文审校:吴逢铁)

1000-5013(2010)05-0503-04

2009-11-10

吴逢铁(1958-),男,教授,主要从事光束传输与控制、超短光脉冲及其非线性效应的研究.E-mail:ftw u@ public.qz.fj.cn.

国家自然科学基金资助项目(60977068);泉州市科技计划重点项目(2009G4)