地方财政收入的组合预测模型研究

陈荣保吴 静

(1.常州信息职业技术学院 江苏常州 2131642.江苏富深协通数码技术有限公司 江苏常州 213003)

地方财政收入的组合预测模型研究

陈荣保1吴 静2

(1.常州信息职业技术学院 江苏常州 2131642.江苏富深协通数码技术有限公司 江苏常州 213003)

由于地方财政收入预测受到诸多因素的影响，而现有的预测方法不尽科学，因此提出了二次组合预测方法。首先通过灰色关联分析确定影响较大的外生变量，然后利用神经网络对选择出的外生变量的预测结果进行组合预测，最后将该组合预测结果与单项预测方法加权平均形成二次组合预测模型。实验证明该方法在地方财政收入预测中是切实可行的。

地方财政收入;灰色关联分析;神经网络;二次组合预测

地方政府的财政预算收入主要由税务部门负责组织，主要的税种科目归国税以及地税部门征管，而其它的非税收入，如国有企业资产经营收益、亏损补贴等则由相关的财政部门负责征收。地方财政收入的总量是政府制定财政预算，编制财政支出计划的根据和来源，从总量上对预算收入进行把握是财政收入预测模型的首要目标，通过预测模型预见财政收入的未来值以及增长态势，与外部宏观经济模型的预测指标进行比较，以判断财政收支计划的合理性。

由于财政经济系统运行于整个地区的国民经济环境之中，因此，在考虑财政指标的同时，模型还引入了一些财政系统以外的对财政指标变化影响较大的宏观经济指标作为外生变量，首先预测这些宏观指标，然后根据它们的发展趋势，以及与财政重要指标的关联程度来分析和确认财政财力系统主要指标预测的合理性。［1］有一些外生变量参与模型运行，有的则作为输入，起到对模型的扰动作用。这将有助于进行政策分析，分析各种经济政策对财政经济的影响。根据未来的可能，改变各种内部参数，重复运行模型，其仿真结果，既可作为分析评价现行政策的依据，又可以作为制定未来政策的参考。

1 预测模型分析

1.1 分析选择算法

分析选择实际上就是一个模型自变量的选择过程，是模型创建的首要工作也是最重要的工作。在模型自变量选择时一般采用灰色关联分析对所涉及的相关因素进行分析选择。

灰色关联分析方法［2］是用关联度大小来描述事物之间、因素之间关联程度的一种定量方法。即在灰色系统中存在两组随机序列，其中，一个数据序列称为“参考模式”或者“参考序列”，另一个序列为关联序列，灰色关联分析方法就是考察关联序列与参考序列的相关性。

参考序列包含有n个特征项(可视为时间序列)，表示为:

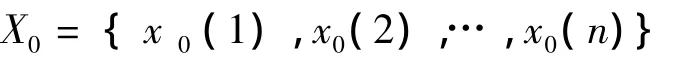
关联序列也包含有n个特征项，表示为

将一系列X1序列设定为X0的影响因素。则X1与X0的灰色关联度定义为:

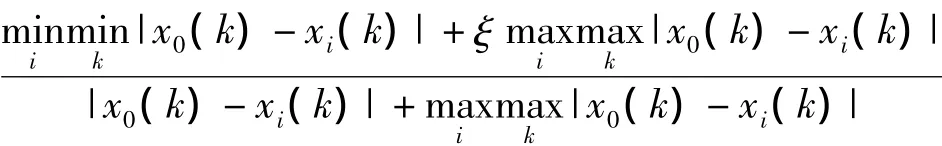
式中ξ是关联权重，

且ξ∈［0，1］，通常取0.5。灰色关联度可理解为各相关联数列构成的项与参考数列对应项间的相对空间距离。灰色关联度越大，它们之间的相对空间距离越小，说明两序列的趋势相近，反之亦然。因此，以灰色关联度的大小和差异程度为标准来选取主要影响因素。

1.2 单一预测模型

1)灰色预测。灰色模型(Grey Model)是用时间数据序列建立系统的动态模型。它把一组离散的、随机的原始数据列经过m次累加生成规律性的累加生成序列，从而弱化原始序列的随机性;然后对累加生成数列建模，最后进行m次累减还原成预测值。具体的算法步骤参考文献［1］。灰色模型具有以下特点:建模所需信息较少，通常只要有四个或以上数据即可建模;样本数据分布特征不局限于正态分布等典型分布;计算方法简便，计算工作量小;建模精度较高，可保持原系统的特征，能较好的反应系统的实际情况。

2)移动平均。移动平均模型是一种常用的随机时序模型，它在经济预测过程中既考虑了经济现象在实践序列上的依存性，又考虑了随机波动的干扰性，对于经济运行短期趋势的预测准确率较高，是近年应用比较广泛的方法之一。它的基本思想是:将预测对象随时问推移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列。这个模型一旦被识别后就可以从时间序列的过去值及现在值来预测未来值。

3)指数平滑。指数平滑法适用于具有或不具有季节变动的反复预测，是一切反复预测中最简易的方法。从实践中我们都有这样一个论点，对于未来发生的事情，最新观察值将比较早期观察值包含更多的信息。因而在预测时，最新观察值应比较早期观察值具有更大的权数。指数平滑法可以满足这一论点。

设时间序列为y1，y2，…，yt，…，则一次指数平滑公式为:

预测模型为:

即以第t周期的一次指数平滑值作为第t+1期的预测值。

时间序列模型在财政收入预测中是一项“性价比”较好的方法，而且由于一般来说如我国这样的国家，经济周期受国家政策调整和管控的影响较大，并不会发生过于突然的变化，因此时间序列模型在我国地方财政收入预测模型构建中具有很强的适用性;此外，由于预测模型的使用和选择与地方政府的相关人员在统计学以及相关科学方面的能力和水平有很大关系，因此引入较简单易懂的时间序列预测模型也有很大的实用性。

不管是上文所介绍的指数平滑还是移动平均模型，都是时间序列模型，属于定量预测模型的一种，这种模型也可以叫做趋势外推模型，主要依赖于对时间序列的分析，通过数学公式度量历史数据的权重，从而预测未来值。序列的过去变化趋势是未来值预测的重要来源。这种趋势外推的预测方法具有成本较小，易于掌握，简单直接的特点，因此应用较为广泛。而这种方法的主要兴起的原因之一就在于它使得地方政府能够从对判断性方法的依赖中解脱出来组合方式。

时间序列模型在财政收入预测中是一项“性价比”较好的方法，而且由于一般来说如我国这样的国家，经济周期受国家政策调整和管控的影响较大，并不会发生过于突然的变化，因此时间序列模型在我国地方财政收入预测模型构建中具有很强的适用性;此外，由于预测模型的使用和选择与地方政府的相关人员在统计学以及相关科学方面的能力和水平有很大关系，因此引入较简单易懂的时间序列预测模型也有很大的实用性。

4)BP神经网络。BP神经网络是一种多层前馈神经网络，层间神经元实现全连接，即下层的每个神经元与上层的每个神经元都实现权连接，而层内各神经元间无连接。典型的BP网络由3层构成，即输入层、隐含层和输出层。它以一系列的输入和理想的输出作为训练的样本，采用误差反向传播方法训练网络节点权重和阀值，通过节点权重的调节使误差精度到达允许的范围，从而建立输入输出的映射关系。训练成功的BP网具有良好的泛化能力。具体的BP算法步骤参考文献［2］。

1.3 组合算法

组合方式是组合预测模型形成的一个关键点。回顾研究国内外大量关于地方财政收入预测方法，归纳总结出了一种新的组合思想:二次组合预测。

第一次组合时，充分考虑外生变量对地方财政收入的影响，具体为:利用往年影响因素值作为输入，待预测指标的实际值作为输出，利用神经网络进行训练模拟，最后通过各个影响因素针对性的预测，根据训练出的神经网络结构得出预测结果如图1。

图1 一次组合示意图

第二次组合时，充分考虑了单向预测方法在预测某些经济指标时候的优势，具体表述为:分别利用各种单一预测方式，对待预测指标进行预测，之后将这些用不同方法预测得到的预测值与第一次组合预测的结果加权平均，以期得到更为精确的预测值如图2。多种预测方式加权组合模型为:设表示第i种预测方法对问题的第t期的预测值。对通过k种预测方法所得到的预测值进行加权平均，得，其中，为权重，并满足在本文中，使用的加权算法具体步骤见参考文献［3］。

图2 二次组合示意图

2 组合建模及预测

2.1 一次组合模型——多因素神经网络组合预测

以江苏某市地方财政收入为例进行分析，由于财政经济系统运行于整个地区的国民经济环境之中，因此，在考虑地方财政收入具体来源的同时，还需要引入对这些因素影响较大的一些宏观经济指标作为外生变量，这些外生变量为:GDP X1、全社会固定资产投资X2、工业企业实现利润X3、全社会消费品零售总额X4、职工工资X5、储蓄额X6、第二产业总产值X7、第三产业总产值X8、出口额X9、进口额X10、工业总产值X11、批发零售总额X12。

1)确定主要指标。由上所述，我们发现影响地方财政收入的值很多，如果全部放入模型考虑，模型会异常庞大且效率不高。此外我们还可以发现地方财政收入的变动过程是一个复杂的、系统的过程，其中部分信息已知，部分信息未知，是一个典型的灰色系统。将地方财政收入体系视为一个灰色系统，其中地方财政收入为参照序列X0，其各项组成指标以及外生变量为关联序列Xi(i=1，2，…，12)。这样就能根据数据依据特定算法计算关联序列和参照序列间的灰色相关度ηHi(i=1，2，……，12)，对计算后的结果按照降序排序，若增值税所对应灰色关联度最大则说明增值税的变化趋势跟地方财政收入的变化趋势最越相近。［4］灰色关联度计算结果:

因为该排序中前五个与后面相差很大，选择取用前5个因素作为主要因素，分别为:GDP、全社会固定资产投资、职工工资、全社会消费品零售总额、储蓄额。

2)预测各项主要指标。对这九个因素利用移动平均法进行预测其在2009年以及2010年的值。结果如表1:

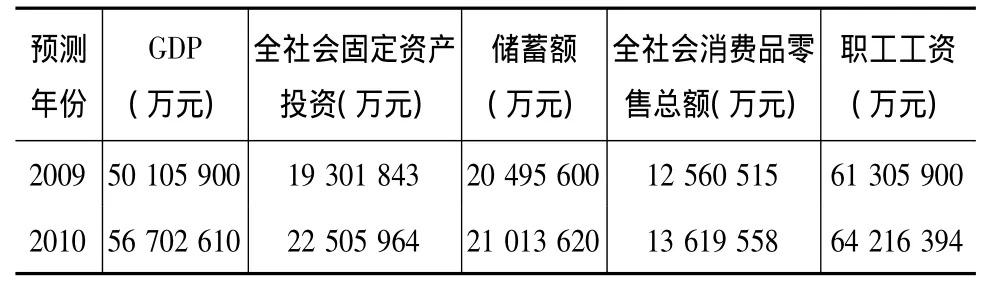
表1 预测指标

3)利用神经网络进行地方财政收入预测。模型将上述9个主要指标作为输入，将地方财政收入值作为输出，调整隐含层节点数使得输出误差最小，达到最佳收敛效果。最后隐含层节点数定为7。预测得到的09年以及10年的地方财政收入为表2:

表2 预测结果

2.2 二次组合模型——加权平均组合预测

Step1:灰色预测模型预测地方财政收入

根据地方财政收入历年的样本数据，采用GM (1，1)模型预测历年以及09、10年的地方财政收入值，得到预测值为，其中n=14。

Step2:移动平均模型预测地方财政收入

设置移动项目为2，得到的预测值为:

Step3:指数平滑模型预测地方财政收入

当平滑系数α设置为0.35时，拟合效果最佳，得到的预测值为

Step4:加权设置

依据参考文献［3］的组合规则，对上述三种单一预测得出的结果以及一次组合预测的结果加权平均，0.659 7，0，0，0.340 3。因此组合预测模型为:

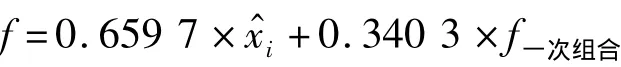
误差率为:27.3;最大误差为:3.24%。

3 结束语

本文归纳得出了新的组合预测思路:二次组合预测，并且将其应用于针对某个城市的地方财政收入的预测。

该模型充分考虑了外生变量对地方财政收入结果预测的影响，以及单项预测模型进行某些经济项目预测时的优势。通过对该种组合模型进行的实验，得到了模型往年数据的误差率，结果表明:虽然一次组合预测方法考虑了外生变量，比较全面，但是由于政策原因，从1994年财政结构起了较大变化，因此只能取用1994年以后的数据，这样就导致数据量不是很充分，使得利用神经网络的模拟存在一定的误差。而在这基础上的二次组合预测除了兼顾外生变量之外，组合了一些适用于短期预测的统计类方法，使得预测准确率大为提升。

［1］ 李洪心，易允文.财政预测模型研究及应用［J］.信息与控制，1997(3):215-220.

［2］ 邓聚龙.灰预测与灰决策(修订版)［M］.武汉:华中科技大学出版社，2002.

［3］ 高隽.人工神经网络原理及仿真实例［M］.北京:机械工业出版社，2003.

［4］ 蒋良奎.组合预测权系数的一种计算方法［J］.上海海运学院学报，1996(2):90-95.

Research on Combination Forecasting Model of the Local Financial Revenue

CHEN Rong-bao1WU Jing2
(1.Changzhou College of Information Technology，Changzhou 213164，2.Jiangsu Finstone Digital Systems Co.，Ltd.，Changzhou 213003，China)

The local financial revenue is affected by many factors and there are some disadvantages in current forecasting methods. Therefore，the secondary combination forecasting model is put forward.First，the main factors for local financial revenue are confirmed via gray correlation analysis.Then the combination forecasting results from neural network and the first step＇s results is obtained.In the end，by weighed average function，the first combination forecasting result is combined with the results of the methods using only one algorithm，and the secondary combination forecasting model is created.Experimental results demonstrate the availability and feasibility of the model in the local financial revenue forecasting.

local financial revenue;Grey Association analysis;neural network;secondary combination forecasting

book=159,ebook=159

TP 182

A

1672-2434(2010)06-0027-04

2010-05-23

陈荣保(1957-)，男，副教授、高级工程师，从事研究方向:计算机应用