基于椭圆曲线的 ELGamal数字签名方案
2010-09-07伍红梅
伍红梅
(西南交通大学数学学院,四川 成都 610031)
基于椭圆曲线的 ELGamal数字签名方案
伍红梅
(西南交通大学数学学院,四川 成都 610031)
首先介绍了有限域上的椭圆曲线,把 ELGamal数字签名体制成功的迁移到基于椭圆曲线的体制上,并在此基础上,给出了两个新的椭圆曲线 ELGamal数字签名方案,提高了签名的安全性,及其签名的效率。
椭圆曲线;数字签名;加密算法
1 引言
20世纪 80年代中期,Miller[1]和 Koblitz[2]将椭圆曲线引进了密码学中,人们对其做了大量的研究工作后,建立了椭圆曲线公钥密码体制。它是一种基于椭圆曲线离散对数问题的公钥密码,并且具有很好的安全性。
椭圆曲线数字签名技术在现代网络数据通信处理过程中扮演着非常重要的角色,在网络资源非常有限的情况下,如何提高网络数据通讯效率及安全,提高签名效率,就显得尤为重要。文献 [3]提出了椭圆曲线数字签名算法,文献 [4]给出了著名的椭圆曲线的数字签名方案,文献 [5]提出了 ELGamal数字签名体制。本文把 ELGamal数字签名体制成功的迁移到基于椭圆曲线的体制上,并在此基础上,给出了两个新的椭圆曲线 ELGamal数字签名方案,提高了签名的安全性及其效率。
2 有限域上的椭圆曲线[6]
(1)GF(p)上的椭圆曲线
GF(p)是一个特征为 p的有限域。p≠2,3。a,b∈GF(p)满足 4a3+27b2≠0。椭圆曲线E(a,b)定义为满足方程 y2=x3+ax+b的点 (x,y)∈GF(p)×GF(p)和无穷远点O的集合。这些点在如下定义的加法下构成一个阿贝尔群,其恒等元为O。P和Q是 E(a,b)上的两点,如果 P=O,则 -P=O,且P+Q=Q+P=Q;令P=(x1,y1),Q=(x2,y2)则 -P=(x1,-y1),P+(-P)=O如果Q≠-P,则 P+Q=(x3,y3),且


(2)GF(2m)上的椭圆曲线
非超奇异椭圆曲线 E(a,b)(GF(2m))定义为满足方程 y2+xy=x3+ax2+b的点(x,y)∈GF(P)×GF(P)和无穷远点O的集合,a,b∈GF(2m)且 b≠0,这些点在如下定义的加法下构成一个阿贝尔群,恒等元为O。P和Q是 E(a,b)(GF(2m))上的两点,如果 P=O则 -P =O,且 P+Q=Q+P=Q;令 P=(x1,y1),Q=(x2,y2)则 -P=(x1,y1+x1),P+(-P) =O;如果Q≠-P,则 P+Q=(x3,y3),且
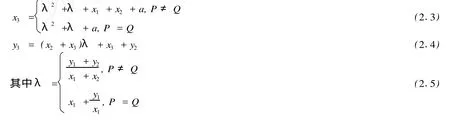
3 椭圆曲线数字签名体制
3.1 椭圆曲线的 ELGam al数字签名算法的参数
构造椭圆曲线 E(a,b)(GF(q)),选取一个基点G,阶是 g,即 gG=O(其中 nG表示为 n个G相加,即 gG=G+G+G+…+G相加,O表示椭圆曲线方程的无穷远点),n为素数,且 n> 3,在区间[1,n-1]中选择一个随机整数 d是签名私钥,Q=dG是签名验证公钥,H是一个安全的 hash函数,公开 q,a,b,g,G,Q,H保密 d。
3.2 签名生成
签名者A lice利用上面的参数和公私钥对消息m签名:
(1)A lice随机选择一个整数 k使得 gcd(k,g)=1;
(2)计算 R=kG=(x1,y1),r=x1modn,如果 r=0则返回到第 (1)步;
(3)计算 k-1modn;
(4)计算 e=H(m);
(5)计算 s =k-1(e-dr)(m odn),如果 s =0则返回到第 (1)步;
(6)将数字签名 s=(e,r,s)传送给 B ob。
3.3 验证过程
(1)B ob收到数字签名 s=(e,r,s),并取得 A lice的公钥 (E/Fq,G,Q);
(2)计算 e=H(m);
(3)计算V1=r Q+sR,V2=eG。
(4)若 V1=V2则验收,否则拒绝。
证明:V1=V2:
V1=r Q+sR=rdG+k-1(e-dr)kG=(rd+e-dr)G=eG=V2 证毕
4 改进的椭圆曲线的 ELGam al数字签名
4.1 方案一
椭圆曲线域参数跟前面介绍的相同,签名过程:
签名者A lice利用上面的参数和公私钥对消息m签名:
(1)A lice随机选择一个整数 k使得 gcd(k,g)=1;
(2)计算 R=kG=(x1,y1),r=x1m odn,如果 r=0则返回到第 (1)步;
(3)计算 e=H(m);
(4)计算 s =k+edr(m odn),如果 s =0则返回到第 (1)步;
(5)将数字签名 s=(e,r,s)传送给 B ob。
验证过程
(1)B ob收到数字签名 s=(e,r,s),并取得 A lice的公钥 (E/Fq,G,Q);
(2)计算 e=H(m);
(3)计算V1=sG-R,V2=er Q。
(4)若 V1=V2则验收,否则拒绝。
证明:V1=V2:V1=sG-R=(k+edr)G-R=kG+er Q-R=er Q=V2 证毕
4.2 方案二
椭圆曲线域参数跟前面介绍的相同,签名过程:
签名者A lice利用上面的参数和公私钥对消息m签名:
(1)A lice随机选择一个整数 k使得 gcd(k,g)=1;
(2)计算 e=H(m);
(3)计算 C1=kG=(x1,y1),r=x1m odn,如果 r=o则返回到第 (1)步;
(4)计算 kQ =(x2,y2),t=x2m odn,如果 t=0则返回到第 (1)步,C1=e+t;
(5)将数字签名 s=(C1,C2),传送给 B ob。
验证过程
(1)B ob收到数字签名;
(2)计算 e=H(m);
(3)计算 e=C2-dC1。
签名验证的证明:e=C2-dC1=e+kQ-dkG=e+kQ-kQ=e
5 结果分析
ELGam al算法其安全性是依赖计算有限域上离散对数问题的困难性,而把 ELGam al数字签名体制迁移到基于椭圆曲线的体制上,其安全性是依赖椭圆曲线离散对数问题。攻击者试图通过分析(e,r,s)来取得签名者的私钥 d,是椭圆曲线上的离散对数问题求解,是困难的。
改进的两个新方案,签名和验证过程中都不含有求逆运算,相对原来的方案提高了签名的速度。显然,该方案的安全性与原方案的安全性相同,都是基于椭圆曲线上的离散对数问题求解,但速度提高了很多。因为椭圆曲线密码体制有着独特的优越性,所以可被应用在需要较短密钥的应用中。
[1]N Koblitz.Elliptic Curves Cryptosystems[J].M ath Comp.1987,48(177):203~209.
[2]V Miller.Usesof Elliptic Curves in Cryptography[A].Advance in Cryptology-CRYPTO,Lecture Notes in Computer Science[M]Springer-Vedag,1986:417~427.
[3]ANSI X9.62.Public Key Cryptography for the Financial Services Industry:The Elliptic CurvesDigital Signature Algorithm(ECDSA)[S].
[4]Johson D Menezes A.The elliptic curve digital signature algorithm [J].Technical Report,CORR99-31,Canada:Department of Combinatorics and Optim ization,University of W aterloo,1999.
[5]ELGamal L.A Public Key Cryptosystem and a Signture Scheme Base on Discrete Logarithm [J],IEEE Transactions on Infor m ation theory,1996,31:469—472.
(责任编辑 刘洪基)
ELGamalD igital Signature Scheme Based on the Elliptic Curves
W U Hong-mei
(School of M athematics,Southwest Jiaotong University,Chengdu610031,China)
The author introduced the elliptic curves over finite fields,put ELGamal digital signature scheme into a successfulmove to a system based on elliptic curve,And on this basis,ELGamal digital signature scheme of two new elliptic curves had been given to improve the security of the signature and the signature efficiency.
elliptic curve;digital signature;encryption
TP309
A
1671-7406(2010)03-0044-04
2010-01-05
伍红梅 (1983—),女,籍贯四川,研究方向密码学。
