混合智能算法在模糊规划中的应用

裴振奎, 陈继东, 赵艳丽, 刘 真

(中国石油大学(华东)计算机科学系 山东东营257061)

混合智能算法在模糊规划中的应用

裴振奎, 陈继东, 赵艳丽, 刘 真

(中国石油大学(华东)计算机科学系 山东东营257061)

简要介绍了模糊规划并综述了模糊规划的建模理论,提出在原有混合智能算法研究的基础上将进化策略融合进混合智能算法中来解决原有算法易陷入局部最优解的问题,提高了求解精度及收敛速度.

进化策略;模糊规划;混合智能算法

0 引言

当今时代,信息作为人类交流的载体,越来越受到人们的关注,在人类发展和科技进步的进程中,信息更是为我们提供了知识的源泉.可以说,信息在当今社会中起到了至关重要的作用.然而人们接触到的信息大多是不确定的,表现为随机性、模糊性、粗糙性、随机模糊性、随机粗糙性等多重不确定性.对于数学中含有的不确定参数的规划,传统的经典优化理论往往无法解决,需要考虑用一些智能算法如人工神经网络、进化算法等构造成混合智能算法并通过计算机程序来进行不确定规划的求解,本文讨论的就是一类表现为模糊性的不确定规划.

1 模糊规划模型

目前,广泛应用的模糊规划模型有3种.

1.1 期望值模型

优化问题中出现的不确定变量相应地都有该变量的数学期望的概念.基于此,第一种建模方法是在期望值约束成立下极大化这些不确定目标函数的数学期望,亦即期望值模型[1]

其中,x为决策向量,ξ为模糊变量,f(x,ξ)表示目标函数,gj(x,ξ),j=1,2,…,p表示模糊约束函数,E表示期望值算子.

1.2 机会约束规划

借用随机机会约束规划的思想,Liu和Iwamura给出了模糊机会约束规划的理论框架[2-3],其允许所作决策在一定程度上不满足约束条件,但该决策使约束条件成立的概率或可能性不小于某一置信水平.典型的机会约束规划可以表示成

其中,x是决策向量,ξ是模糊参数,α和β分别是对约束和目标事先给定的置信水平,Cr{}表示{}中事件成立的概率或可能性.

1.3 相关机会规划

一个复杂的决策系统通常要完成多项任务,称之为事件,决策者往往希望这些事件实现的概率或可能性(机会函数)尽可能的大.相关机会规划是使事件的机会函数在不确定环境下达到最大的优化理论[4].不确定环境下典型的相关机会规划可以表示为

其中,x是一个n维决策向量,ξ是一个模糊向量,f(x)是一个事件的机会函数,gj(x,ξ)≤0,j=1,2,…,p是不确定环境.

2 应用进化策略改进的混合智能算法

2.1 传统的混合智能算法

对于不确定优化,智能算法包括神经元网络、模拟退火以及遗传算法等,为了提高效率,可以将几种方法有效地结合起来,从而形成混合智能算法.文[5]把神经元网络和遗传算法有机地结合起来,首先使用模拟产生训练样本,然后利用这些数据训练神经网络逼近不确定函数,最后把神经元网络嵌入到遗传函数,从而得到混合智能算法,其过程如下:

步骤1)用模拟产生一组数据,即训练样本.

步骤2)训练神经元网络以便逼近不确定函数.

步骤3)初始产生pop_size个染色体,使用前面训练的神经元网络检验染色体的可行性.

步骤4)对染色体进行交叉操作以及变异操作,用神经元网络检验后代的可行性.

步骤5)使用神经元网络计算所有染色体的目标值.

步骤6)根据目标值计算每个染色体的适应度.

步骤7)旋转赌轮,选择染色体.

步骤8)重复步骤4～7,直到给定的次数.

步骤9)最好的染色体作为优化问题的最优解.

2.2 改进的混合智能算法

其中步骤3～9是利用遗传算法来对函数进行解优化,本文就是针对这一过程做出改进,将进化策略、模拟退火算法和遗传算法有效地结合起来,达到寻优操作,既能跳出局部最优解,又能保证收敛速度的良好效果.

单纯的遗传算法存在这些局限性[6]:它不能保证所得到的是最佳答案;标准遗传算法并不保证全局最优收敛,只能在一定的约束条件下实现全局最优.单纯的进化策略存在这些局限性[6]:每一维常数的标准偏差(平均步长)使收敛最优值的速度变慢;点对点搜索的不稳定性可能造成停止于局部最小值.因此考虑将两者结合,构造一种新的混合智能算法并应用在模糊规划中.

该算法以遗传为基础,将进化策略作为一个独立算子,其中引入了进化策略的(μ,λ)选择算子,提高算法跳出局部最优的几率,在算子的变异过程中采用模拟退火的思想,精英保留策略的应用能够保证算法收敛到全局最优.两种算法相互借鉴,起到互补的作用.

2.3 改进算法的基本思想

步骤1)产生初始群体 随机生成初始群体,并利用神经元网络对其进行可行性的检验.编码方案采用实数编码.

步骤2)交叉 随机选取两个配对个体进行交叉,然后随机生成一个0或1标志数,若标志数为“1”,则对两个个体中相应位的基因进行负交叉运算;否则对两个个体中相应位的基因进行正交叉运算.

步骤3)变异 对个体中的每个基因都随机生成一个P,P属于[0,1],若满足P>Pm(Pm为变异概率),则对该位的基因进行变异操作;否则保持不变.下面应用模拟退火思想,对变异结果,按照Metropolis接受准则判断接受与否,即:发生变异的个体与其变异后的个体适应度值进行比较,若变异后个体较优则接受其作为新个体,并替代变异前个体;否则随机产生一个随机数r,若满足exp(f1-f2/T)>r,则接受变异后个体作为新个体,其中f1为变异前个体的适应值;f2为变异后个体的适应值;T为退火温度,退火函数为T=T0＊Sgen,T0为初始温度,S为退火系数,gen为进化代数.若上面两个条件都不满足则不接受新个体.

步骤4)进化 在旧个体基础上增加一个随机量,从而形成新个体,这个随机量由步长σ∈Rn(正态分布的标准差)构成,可以用来调整对个体进行变异操作时变异量的大小.根据进化策略的思想[7],假设群体的个体X={x,s}经过变异运算后得到一个新的个体X′={x′,s′},则新个体的组成元素是

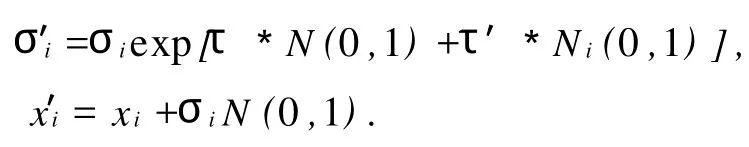
其中,i=1,2,…,n,N(0,1)和Ni(0,1)是均值为0、方差为1的正态随机变量,t和t′是算子集参数,τ=和τ′=,τ＊N(0,1)和τi＊Ni(0,1)分别表示变异时的整体步长和个体步长.

步骤5)选择 选择不采用轮盘法那种随机方式,而是采用进化策略中以确定方式进行的选择算子(μ, λ)选择,是优良个体100%被保留,劣质个体100%被淘汰.在新产生的λ个个体中选取μ个最优者,将它们保留到子代群体中,该选择方式易于跳出局部最优解,而且能够扩大群体多样性,从而有效避免未成熟收敛.

保留迄今为止存在的最优个体,保证其不被交叉和变异等遗传算子破坏.具体操作为:计算新群体的适应值,若新群体中的最优个体优于上代保存的最优个体,则用该个体替换上代保留的最优个体;否则用上代的最优个体替换新群体中最差的个体.

3 数值试验

分别对3种模型进行试验:

①首先考虑模糊期望值模型

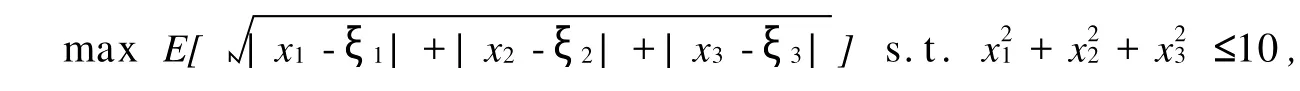
其中,ξ1,ξ2和ξ3分别是三角模糊变量(-4,-2,0),(-2,0,2)和(0,2,4).通过运行该算法1 000代,找到了最优解:x＊1=-1.778 4,x＊2=-1.881 3,x＊3=-1.824 3,其目标值为3.81.只用遗传算法进行解优化所取得的最优目标值是3.77.

②考虑带有模糊系数的单目标机会约束规划

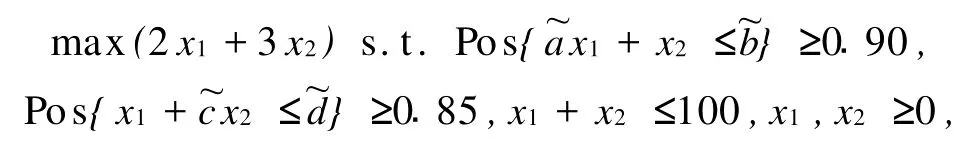
③考虑模糊相关规划模型

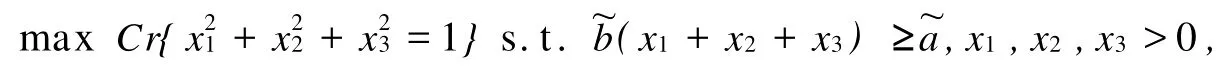
用染色体V=(v1,v2)表示模型的一个解,它可按x1=v1,x2=v2,x3=方式进行解码.

4 结论

采用混合智能算法来解决模糊规划问题是目前广泛使用且有效的计算方法,基于此,本文提出了将进化策略混合进遗传算法中来构造混合智能算法并应用到模糊规划中去.从数值试验的结果可以看出,新算法改良了以往遗传算法中易陷入局部最优解问题.随着技术的不断发展,遗传算法与进化策略两种算法交叉渗透,差异也在不断缩小,通过两者的相互借鉴,必定会产生更多稳定、高效的新算法.

[1] Liu B,Liu Y K.Expected value of fuzzy variable and fuzzy expected valuemodels[J].IEEE Transactionson Fuzzy System s,2002,10(4):445-450.

[2] Liu B,Iwamura K.Chance constrained p rogramming w ith fuzzy parameters[J].Fuzzy Sets and Systems,1998,94(2): 227-237.

[3] Liu B,Iwamura K.A note on chance constrained p rogramming w ith fuzzy coefficients[J].Fuzzy Sets and System s, 1998,100(1/2/3):229-233.

[4] Liu B.Dependent-chance p rogramming in fuzzy environments[J].Fuzzy Sets and System s,2002,109(1):97-106.

[5] Li X,Liu B.Foundation of credibilistic logic[J].Fuzzy Op timization and Decision Making,2009,8(1):91-102.

[6] Li P,Liu B.Entropy of credibility distributions for fuzzy variables[J].IEEE Transactions on Fuzzy Systems,2008,16 (1):123-129.

[7] Gao J,Liu B.Fuzzy multilevel p rogramming w ith a hybrid intelligent algo rithm[J].Computers and Mathematics w ith App lications,2005,49:1539-1548.

[8] Ke H,Liu B.Fuzzy p roject scheduling p roblem and its hybrid intelligent algorithm[J].Applied Mathematical Modelling,2010,34(2):301-308.

[9] 刘宝碇,赵瑞清,王纲.不确定规划及应用[M].北京:清华大学出版社,2003.

[10] 黄华娟,周永权.改进型人工鱼群算法及复杂函数全局优化方法[J].广西师范大学学报:自然科学版,2008,26(1): 194-197.

[11] 张美玉,黄翰,杨晓伟,等.求解线性运输问题的新型进化算法[J].广西师范大学学报:自然科学版,2006,24(4):74-78.

[12] 武志峰,杨蓓.一种改进的粒子群优化算法[J].郑州大学学报:理学版,2007,39(3):109-112.

[13] 李喜艳,张文宁,周清雷.混合编码遗传算法在测试数据生成中的应用[J].郑州大学学报:理学版,2009,41(3):22-25.

Fuzzy Programm ing with a Hybrid Intelligent Algorithm

PEIZhen-kui, CHEN Ji-dong, ZHAO Yan-li, L IU Zhen
(Department of Com puter Science,China University of Petroleum,Dongying 257061,China)

Fuzzy p rogramm ing offers a powerful means of handling op tim ization p roblem s w ith fuzzy parameters.Fuzzy p rogramm ing has been used in different w ays in the past.Fuzzy p rogramming is p resented briefly,and the modeling p rincip le of fuzzy p rogramming is summarized. In o rder to increase the p robability of escaping from the local op tima,a new hybrid intelligent algorithm fused evolution strategies is given,w hich imp roves the p recision and convergence speed. Then the algorithm steps are introduced.Finally,the p rospects and directions for the development of hybrid intelligent algorithm are p roposed.Numerical results show that,the new hybrid intelligent algorithm is superior to the traditional algorithm on accuracy.

evolution strategies;fuzzy p rogramming;hybrid intelligent algorithm

TP 391

A

1671-6841(2010)03-0071-04

2010-01-26

国家自然科学基金资助项目,编号60673089.

裴振奎(1962-),男,副教授,主要从事计算智能、图像处理和机器学习研究,E-mail:peizhk@upc.edu.cn.