具有第二次多选择服务的多重休假M/G/1排队

原小娟, 田乃硕, 赵 媛, 宁小虎, 靳晓青

(燕山大学理学院 河北秦皇岛066004)

具有第二次多选择服务的多重休假M/G/1排队

原小娟, 田乃硕, 赵 媛, 宁小虎, 靳晓青

(燕山大学理学院 河北秦皇岛066004)

研究了具有第二次多选择服务的多重休假M/G/1排队模型.顾客到达是泊松过程,且两次服务时间都服从一般分布.通过引用嵌入马尔可夫链和广义服务时间的方法给出了稳态队长的母函数和等待时间的LST,进而给出模型的特例,最后通过数值例子分析了参数对平均队长和平均等待时间的影响.

连续时间排队;第一次必须服务;第二次多选择服务;多重休假

0 引言

目前,很多学者在M/G/1排队模型的基础上,对具有各种排队规则和服务规则的排队模型进行了深入的研究.M adan研究了一种具有第二次选择服务的M/G/1排队模型后[1],具有第二次选择服务排队模型的研究受到了更多学者的关注,而这些研究多采用了补充变量法求解模型.文献[1]的模型中,顾客接受第一次服务时,服务时间服从一般分布,而接受第二次服务时,服务时间服从指数分布.由于服务时间服从指数分布有其局限性,因此,文献[2]做了改进,把第二次服务时间从指数分布推广到一般分布.尹小玲等[3]把第二次选择服务只有一项服务推广到多种不同的服务可供选择,并且第一次服务时间和第二次选择服务时间都服从一般分布,使用补充变量法研究了批量到达的具有第二次多选择服务的M/G/1排队系统.

近年来,大多数学者的工作都集中在具有第二次选择服务的排队模型,而研究具有第二次多选择服务的排队模型甚少.由于补充变量法比较复杂、繁琐,而广义服务时间方法却有一定的技巧性,因此本文通过引入广义服务时间,使用嵌入马尔可夫链的方法将多重休假引入到具有第二次多选择服务的M/G/1排队模型中.

1 模型描述和嵌入马尔可夫链

模型描述如下:

1)顾客到达遵循参数λ的Poisson过程.

2)在系统中所有到达的顾客都必须在服务台接受第一次服务,称为第一次必须服务,其服务时间S0的分布函数为F0(t),t≥0,其一、二阶矩和LST记为:

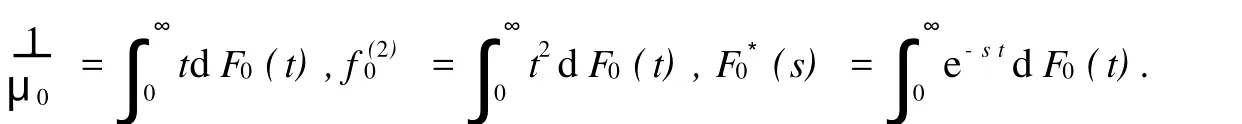
3)第一次必须服务完成后,紧接着顾客以概率γk(1≤k≤m)选择接受m(m≥1)中不同服务中的某一种(不接受第二次服务的顾客则离开系统),称为第二次多选择服务,其服务时间Sk的分布函数为Fk(t), t≥0,其一、二阶矩和LST记为

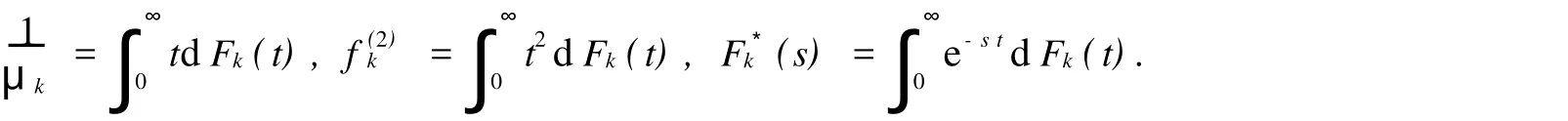
如果令γ0=1,那么γ0表示顾客接受第一次必须服务后离开系统的概率.

将服务员的服务时间分成两部分:第一次必须服务时间S0和第二次多选择服务时间Sk,则

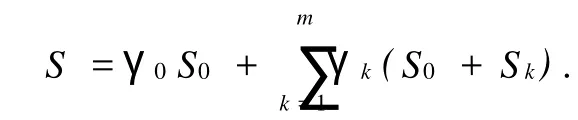
4)系统中一旦无顾客,服务台立刻开始一次随机长度V的休假,结束一次休假时系统中若仍无顾客,服务台就接续一次独立同分布的休假,直到某次休假结束时系统中已有顾客等待,服务台终止休假并开始接待顾客,服务到服务台再次变成空.设休假时间的分布函数为V(x),其LST为:v＊(s)且E(V)与E(V2)存在.

以上随机变量相互独立,另外系统中只有一个服务台且服务机制为先到先服务(FCFS).

以Ln(n≥1)表示第n个顾客离去后瞬时系统内顾客数,则{Ln,n≥1}是队长过程Lv(t)的嵌入Markov链,容易验证,离去时刻的队长{Ln,n≥1}满足递推公式,其中,A是一个服务时间内到达的顾客数,Qb表示一个忙期开始时系统内的顾客数,其中A的分布、母函数与均值分别为:

在确定Qb的分布之前,设vj为一个休假时间内恰好到达j个顾客的概率,其分布和母函数为:

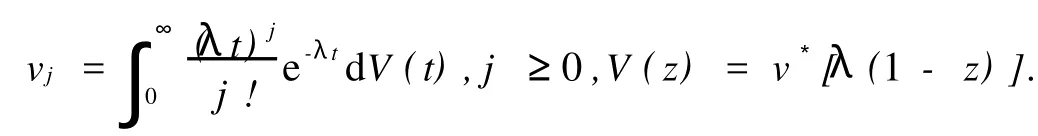
依多重休假策略,则Qb的分布为,其中v0=v＊(λ),则Markov链{Ln, n≥1}的转移概率矩阵为

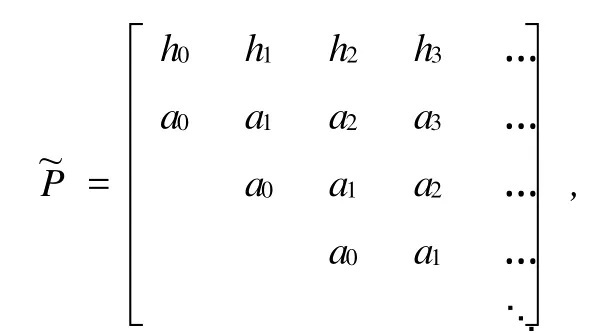
使用Foster准则可以类似的证明{L,n≥1}正常返当且仅当n

2 稳态队长和等待时间

设ρ<1,则{Ln,n≥1}正常返.记

定理1当ρ<1时,具有第二次多选择服务的多重休假M/G/1排队系统中离去时刻的稳态顾客数Lv有母函数

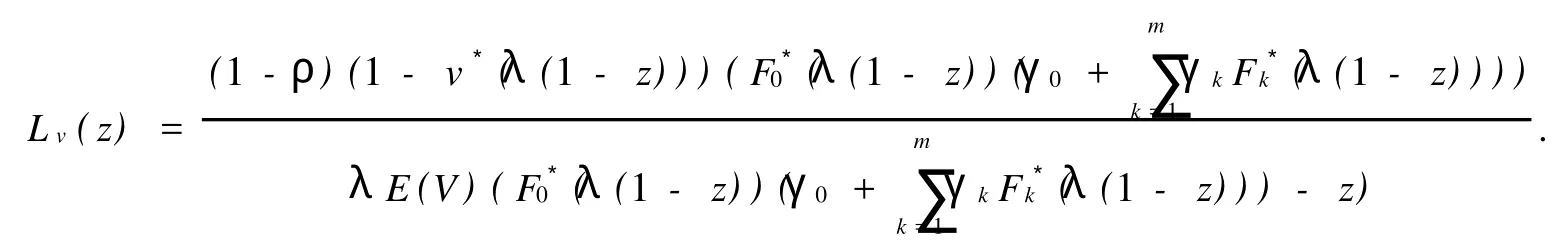
证明当ρ<1时稳态分布存在且满足Π,则π,两边各取母函数,得,经整理并解得到

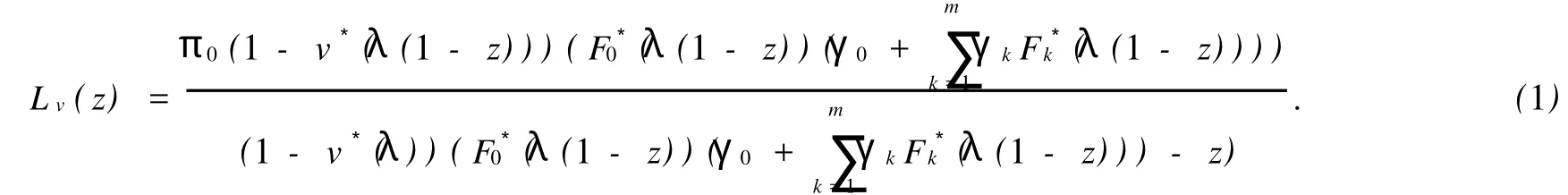
使用正规化条件Lv(1)=1及L’Hospital法则求解可以得到把π0代入(1)式即得Lv(z)的表达式,定理得证.

容易计算离去时刻的平均队长

定理2当ρ<1时,具有第二次多选择服务的多重休假M/G/1排队系统中稳态等待时间Wv的LST为

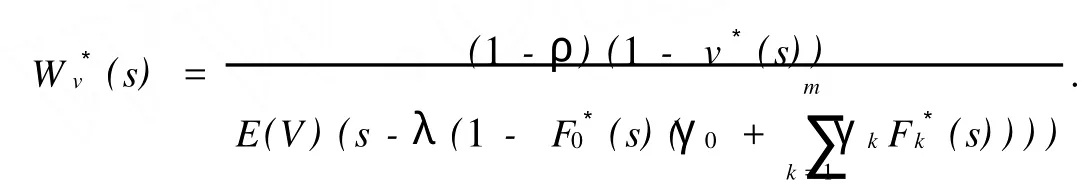
证明一个顾客离去时,留在系统中的顾客数恰好等于它的等待时间Wv和服务时间S内到达的顾客数之和.注意到等待时间与服务时间内到达的顾客数相互独立,于是有

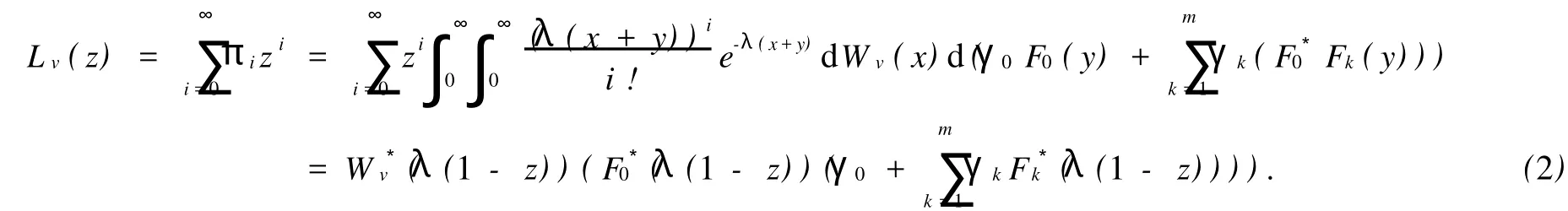
把定理1中Lv(z)的表达式代入(2)式,并令λ(1-z)=s,则得

从而可以计算平均等待时间为

3 特例

例1具有第二次多选择服务的M/G/1排队.

在上述排队模型中取休假时间为零时,系统模型详见文献[3],因此可得

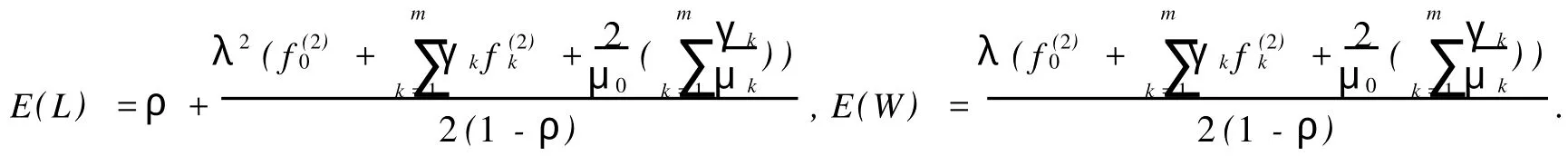
若进一步考虑m=1时,即第二次多选择服务只有一种服务,系统模型详见文献[2],因此可得

例2多重休假的M/G/1排队.

取γk=0时,即没有第二次多选择服务,系统模型详见文献[4],因此可得

4 数值例子

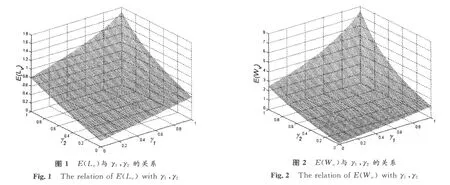
通过以上分析,我们获得了系统的平均队长、平均等待时间等一些稳态指标,但是在实际问题中不仅要知道排队系统的稳态指标,而且还要了解系统中的某些参数对这些稳态指标的影响,从而刻画出排队系统的动态.下面以m=2为例,给出平均队长E(Lv)、平均等待时间E(Wv)随着参数γ1,γ2变化的规律,如图1、图2所示.

[1] Madan K C.An M/G/1 queue w ith second op tional service[J].Queueing Systems,2000,34:37-46.

[2] Medhi J.A single server poisson input queue w ith a second op tional channel[J].Queueing Systems,2002,42:239-242.

[3] 尹小玲,邓永录,刘国柱.具有第二次多选择服务的M/G[x]/1排队系统[J].应用数学与计算数学学报,2003,17(1): 41-53.

[4] 田乃硕.休假随机服务系统[M].北京:北京大学出版社,2001.

[5] 朱翼隽,王成全,陈燕.具有二次可选服务反馈的M[x]/G/1(E,SV)排队系统[J].江苏大学学报:自然科学版,2007,28 (4):363-365.

The M/G/1 Queueing System with Second Multi- optional Servicesand M ultiple Vacations

YUAN Xiao-juan, TIAN Nai-shuo, ZHAO Yuan, N ING Xiao-hu, JIN Xiao-qing
(College of Science,Yanshan University,Qinhuangdao 066004,China)

The M/G/1 queueing system w ith second m ulti-op tional services and m ultip le vacations are discussed.The arrival of customer is a general Poisson p rocess,meanw hile,the first service time and the second service time all have general distributions.Using imbedded Markov chain and the broad sense service timemethod,the generating function of the steady-state queue length and the LST of the w aiting time are derived.Furthermo re,the particular case of this model are obtained.Finally,the effect of the parameterson the expected queue length and the expected waiting time are analyzed by numerical examp les.

continuous time queue;the first essential service;the second m ulti-op tional services; m ultip le vacations

O 226

A

1671-6841(2010)03-0011-04

2009-12-31

国家自然科学基金资助项目,编号10671170.

原小娟(1984-),女,硕士研究生,主要从事排队论及其应用研究,E-mail:456yuanjun123@163.com.