双参数指数分布参数的最短区间估计
2010-09-07周世国张新育
周世国, 张新育, 苏 庆
(郑州大学数学系 河南郑州450001)
双参数指数分布参数的最短区间估计
周世国, 张新育, 苏 庆
(郑州大学数学系 河南郑州450001)
研究了双参数指数分布的区间估计方法.首先讨论了当其中一参数为已知,而另一参数未知时,双参数指数分布尺度参数基于选定枢轴变量的最短区间估计方法;然后讨论了两参数均未知的情况下,参数的最短置信区间估计方法.
双参数指数分布;区间估计;最短置信区间
0 引言
未知参数最短置信区间的估计问题实际上是一个条件极值问题,可以被转化为一个方程组,从而可用数值计算的方法迭代求解.未知参数θ的区间估计与其点估计相比有着明显的优势,它不仅给出了参数真值所在的范围,还给出了该范围包含真值的可信程度.因此在置信水平1-α确定的前提下,置信区间的长度越短越好.如果枢轴量的密度是单峰对称函数,显然当两侧各取α/2时,置信区间长度为最短;如果枢轴量的概率密度非对称,目前常用的方法[1-3]仍是按对称情况来处理,但这样确定的置信区间一般并非最短.本文首先给出总体服从指数分布参数的区间估计方法,然后在此基础上研究最短区间估计的问题.
1 当μ已知时,关于σ的最短置信区间估计
定理1设X1,X2,…,Xn为双参数指数分布总体X~E(μ,σ)的一个简单样本,则
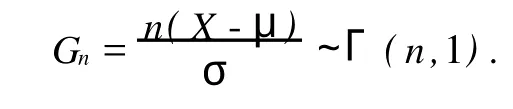
证明因为X~E(μ,σ),故(X-μ)/σ~E(1).
由于m个独立同分布的指数变量之和为伽玛变量[4],即

由定理1知,可以用Gn作为σ区间估计的枢轴量.选取分位点a,b,使P{a 由于n,σ与a,b的选取无关,所以求最短区间问题即化为求解下述条件极值问题 采用Lagrange乘子法[5],令可得 定理2条件极值问题(1)在n≥2时有解,且解唯一. 证明令h(x)=xn+1e-x(x≥0),可知h(x)为单峰函数,且在x0=n+1处达到最大值.由单峰函数的性质可知,只需b>n+1,a f(x,n)与h(x)性质类似,在x0=n-1处达到峰值,当b增加到b0时,对应的a减小到a0=u(b0),所以是关于b单调增加的,易知当b→∞时,u(b)→0;当b→n+1时,u(b)→n+1,故有 所以(1),(2)有唯一的解b*,a*=u(b*),而σ的最短置信区间为 其中a*,b*可通过软件[6]求解方程组得到. 例1已知某种电子元件的使用寿命服从参数为λ的指数分布.现从中抽取10个元件进行寿命检测,获得数据如下(单位:h):1050,1100,1080,1200,1300,1250,1340,1060,1150,1150,求在置信度为95%下的最短置信区间. 求最短区间问题即化为求解条件极值问题: 仍采用Lagrange乘子法,仿照1,可得μ的最短置信区间为,其中a*,b*可通过软件 引理1设X1,X2,…,Xn独立同分布于E(1),X(1),…,X(n)为其次序样本,则 3)X(1),Yr之间相互独立,r=2,3,…,n. 证明 利用次序统计量密度函数公式[4]: 当zr≥0时, 当zr<0时,pZr(zr)=0,所以Zr~E(n-r+1),因此Yr=(n-r+1)Zr~E(1).即证得2)成立.下面证明X(1),Yr之间相互独立,再令Z1=X(1),则只需证明Zr之间相互独立,r=1,2,3,…,n.对于次序统计量X(1),…,X(n),其联合分布函数为 (ⅰ)当zr≥0,r=1,2,…,n时, 所以Zr之间相互独立(r=1,2,3,…,n);即X(1),Yr之间相互独立(r=2,…,n),即证得3)成立. 定理3设X1,X2,X3,…,Xn为来自双参数指数分布E(μ,σ)的一个简单样本,令Y=X(1),S=,则(Y,S)为(μ,σ)的一组充分统计量,且Y,S独立. 证明样本的概率函数为 由因子分解定理[4]可知,是(μ,σ)的一组充分统计量,而显然与(Y,S)之间存在一一对应的关系,所以(Y,S)也是(μ,σ)的一组充分统计量.令,r=1,2,…,n,则T独立同分布于Er(1). 采用Lagrange乘子法,仿照(1)可得σ的最短置信区间为,其中a*,b*通过软件求解方程组得到. 当g<0时,pG(g)=0. 显然这样的a,b不存在,所以上述问题极值在边界达到,比较端点得μ的最短置信区间为X(1)),其中a*由方程得到. 例2以下一组数据(数据选取于参考文献[3])被认为来自双参数指数分布电子元器件的失效时间,求在置信度为95%下的区间估计, 对σ的估计,常规等尾置信区间的分位点计为2.198和11.639. 对μ的估计,常规等尾置信区间的分位点为1.182和230.971;μ的常规等尾置信区间为 [1] 蒋福坤,刘正春.指数分布参数的最短置信区间[J].数理统计与管理,2004(5):43-55. [2] 袁长迎,徐明民.伽马分布参数的最短置信区间[J].数理统计与管理,2006(7):435-437. [3] 周莉.双参数指数分布的比较[J].烟台师范学院学报:自然科学版,2005,21(4):250-253. [4] 罗俊明,代宁,等.概率论与数理统计[M].郑州:郑州大学出版社,2002. [5] 闫战立.微积分[M].北京:高等教育出版社,2007:115-121. [6] 郝黎仁,李宝麟,何凤兰,等.Mathcad 2001及概率统计应用[M].北京:高等教育出版社,2002:50-151. The Shortest Interval Estimates on Exponential Distribution with Two-parameter ZHOU Shi-guo, ZHANG Xin-yu, SU Qing Themethod of interval estimate on exponential distribution w ith two-parameter is studied.Firstly,the shortest confidence interval of scale parameter based on chosen pivot variables for exponential distribution w ith two-parameter is studied on condition that the other parameter has been know n.Then the methods of the sho rtest confidence interval of scale parameters based on chosen pivot variables fo r two-parameter exponential distribution are discussed under the condition that no parameter has been know n. exponential distribution with two-parameter;interval estimate;shortest confidence interval O 212.1 A 1671-6841(2010)03-0001-06 2009-09-10 国家自然科学基金资助项目,编号10671183. 周世国(1971-),男,副教授,硕士,主要从事概率统计理论及其应用研究,E-mail:haoyu1019@vip.sohu.com.




2 当σ已知时,关于μ的最短置信区间估计


3 当μ,σ均未知时,关于μ,σ的最短置信区间估计

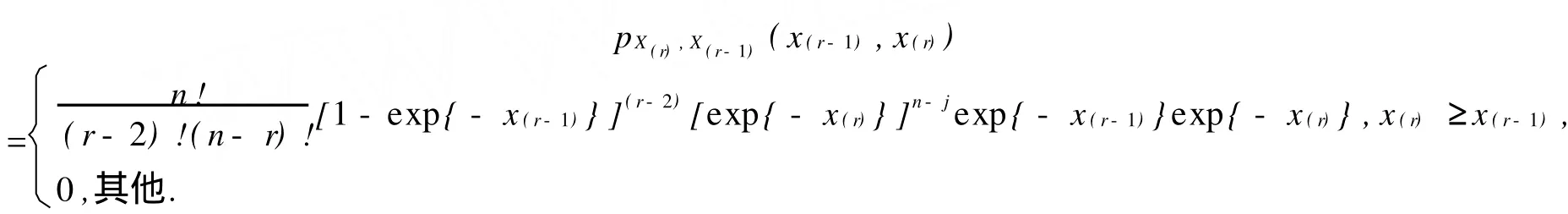




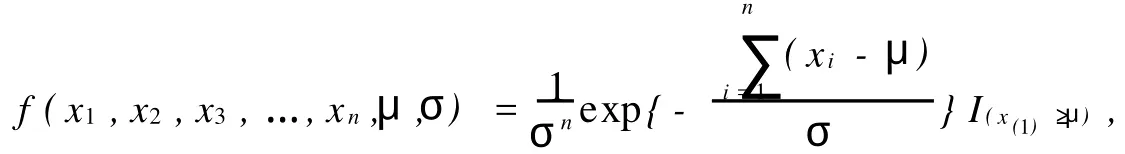

3.1 关于σ最短置信区间估计
3.2 关于σ的最短置信区间估计

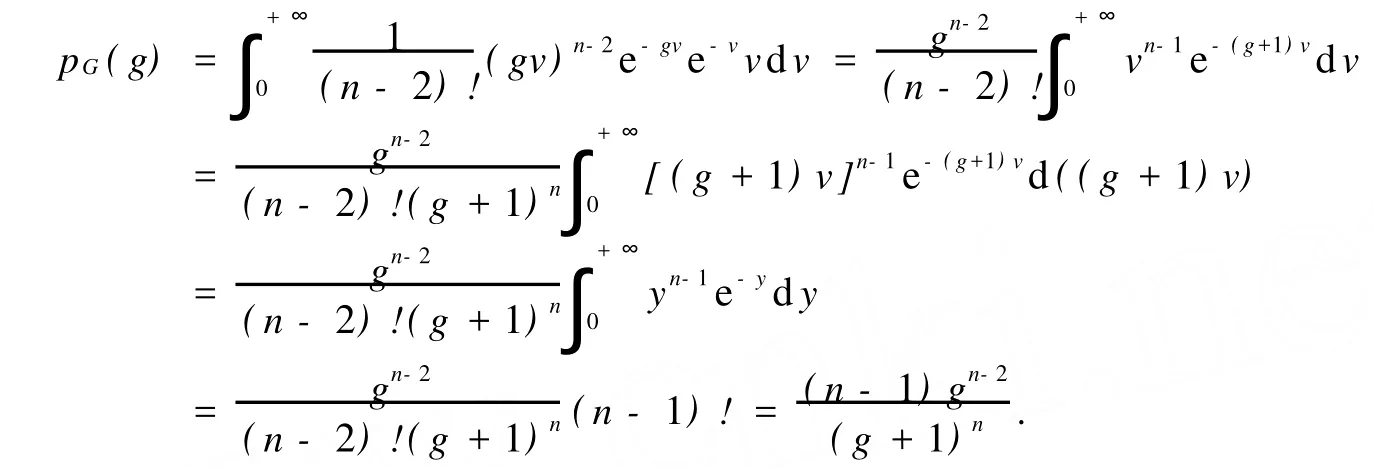
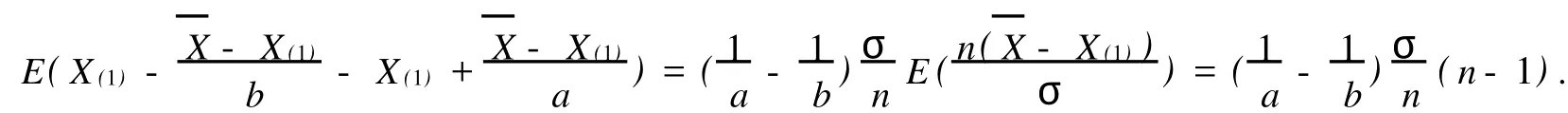
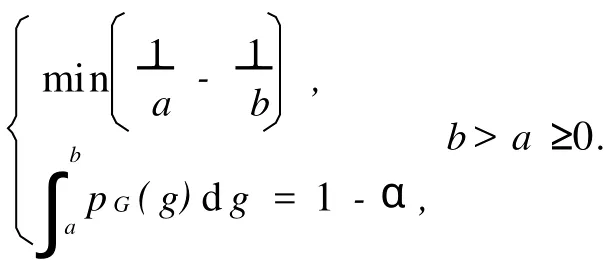
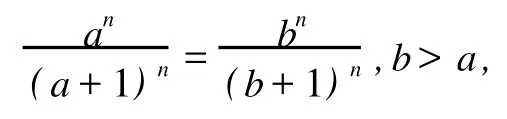
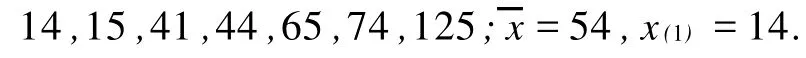
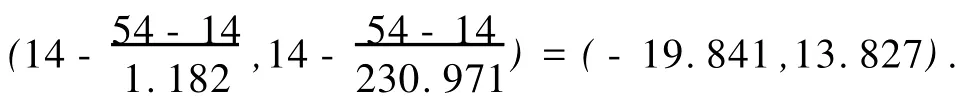
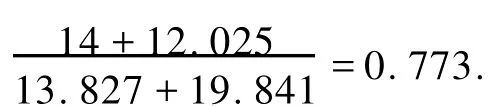
(Department of M athem atics,Zhengzhou University,Zhengzhou 450001,China)
