用山路引理证明拟线性方程组正解的存在性
2010-09-07祁瑞改杨国英
祁瑞改, 杨国英
(河南理工大学数学与信息科学学院 河南焦作454000)
用山路引理证明拟线性方程组正解的存在性
祁瑞改, 杨国英
(河南理工大学数学与信息科学学院 河南焦作454000)
考察了一类带有Dirichlet边界条件的p-Lap lacian方程组的正解.主要用山路引理给出在合适的参数条件下方程组解的存在性,再利用方程的积分不等式等得到解的非负性结论.
p-Lap lacian方程组;山路引理;临界点
0 引言
本文主要讨论下述带有Dirichlet边界条件的p-Laplacian拟线性方程组
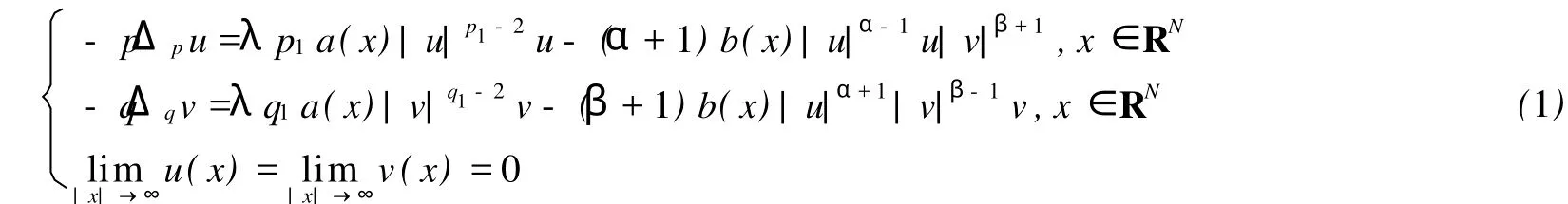
对于含有p-Laplacian的单个方程,正解的存在性和多解性结果很多,主要用到变分法、拓扑度理论等[1-2].对于含有p-Laplacian拟线性椭圆型方程(组)的边值问题,许多学者用上下解方法、爆破方法、纤维方法等讨论了正解的存在性和不存在性[3-5].
本文主要是通过山路引理证明泛涵存在临界点,进而证明方程组(1)存在正解.
1 基本假设
定义Sobolev空间D1,p(RN)和D1,q(RN)是C0∞(RN)分别关于范数
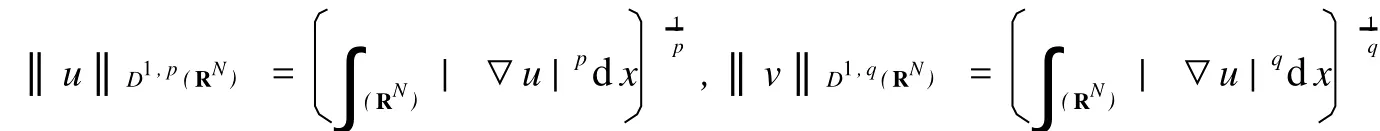

基本假设如下:
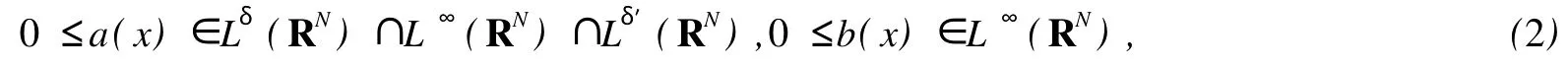
其中,
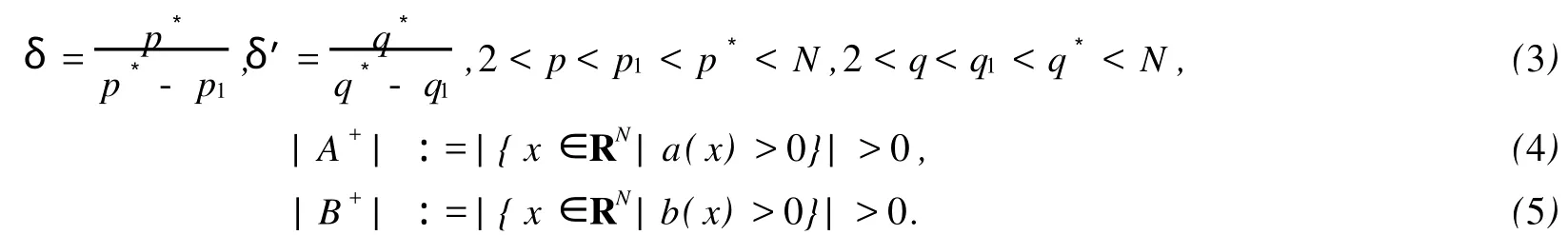
另外,
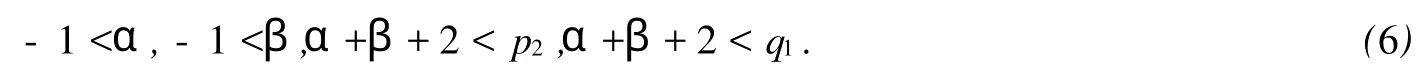
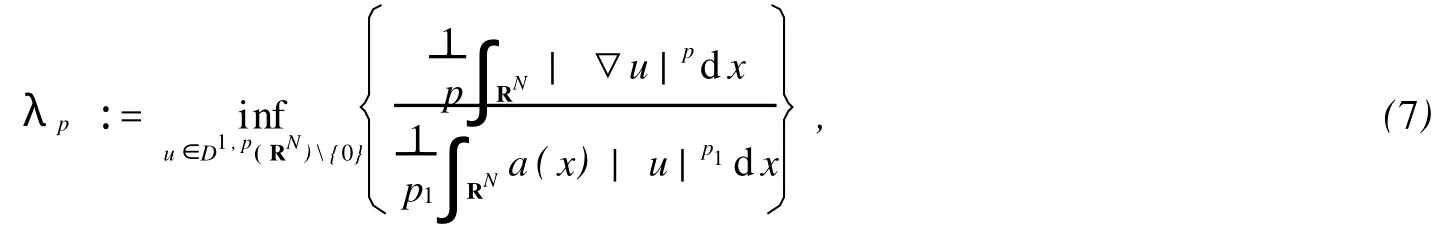
并且相应于λp方程在上存在一正解φ[6].同理,对于方程,记
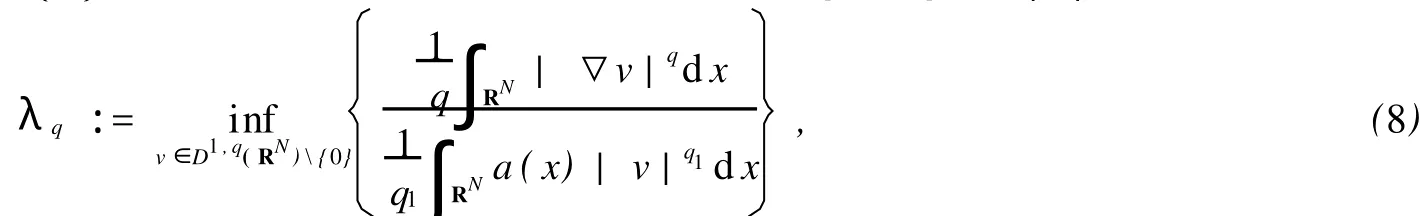
并且相应于λq方程在D1,q(RN){0}上存在一正解ψ.
2 主要结论
首先建立泛函J:D→R如下:
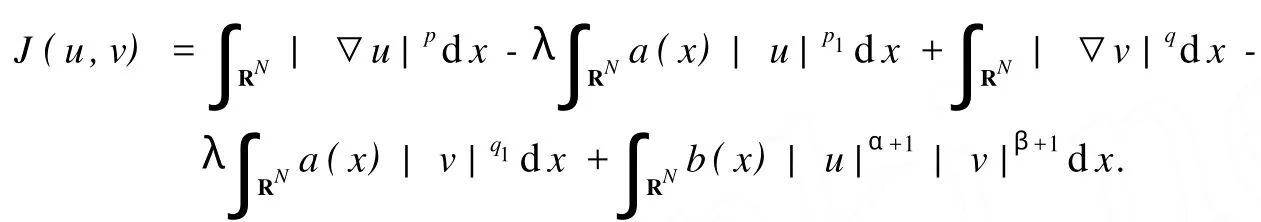
显然,J(u,v)的临界点是方程组(1)的弱解.
引理1当时,存在s>0和t>0,使得时,有J(u,v)≥t成立.
证明令,因此,和两项中至少有一项不小于1,不妨设,从而有
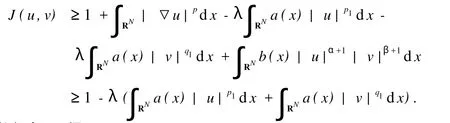
由Hölder不等式和嵌入定理,得
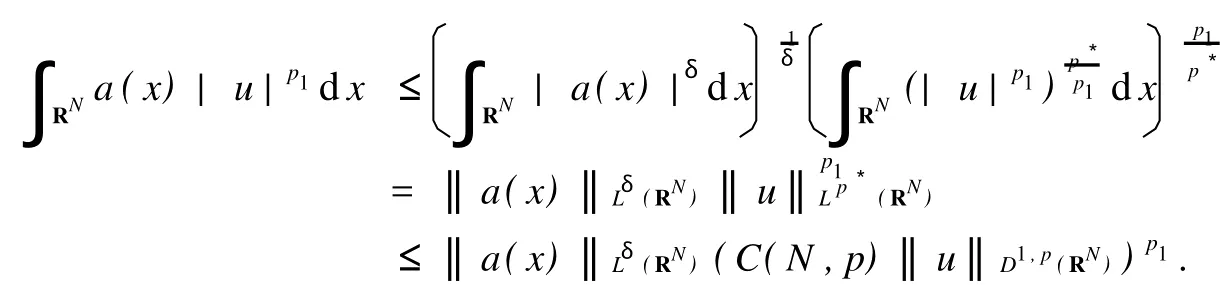
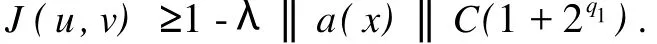
引理2当λ>0时,对任意给定的s>0和t>0,存在(u0,v0)∈D使得‖(u0,v0)‖>s和J(u0,v0) 证明选取,且当x∈A+时,u>0,v>0,对所有的k>0,有 由假设α+β+2 令(u0,v0)=(ku,kv),则总存在充分大的k,使和J(u0,v0) 定理1假设(2)~(6)成立,当 证明易知D=D1,p(RN)×D1,q(RN)是Banach空间,并且J(u,v)是C1(D1,p(RN)×D1,q(RN),R)上满足P.S.条件的连续函数[7-8].在假设(2)~(6)条件下,引理1和引理2显然成立,再由山路引理可得,泛函J存在临界点(′)∈D1,p(RN)×D1,q(RN)使得′(′)=0,J(′)=J(h(t)),其中,h(t)是连接(0,0)和(u0,v0)的一条道路,Φ由D中连接(0,0)和(u0,v0)的所有道路组成,从而(u′,v′)是方程组(1)的弱解. 下面验证弱解的非负性. 记u-=max(0,-u′)≢0,v-=max(0,-u′)≢0,其中,(u′,v′)∈D1,p(RN)×D1,q(RN)是方程(1)的解.对方程组(1)第一个式的两边同时乘以u-,并在RN上积分,得 显然,这与(7)式矛盾,所以u′≥0.同理可证,v′≥0. 显然,(u′,v′)≢(0,0).假设(u′,0)是方程组(1)的解,则u′≥0,且u′≢0.把(u′,0)带入方程组(1),两边同时乘以u′,并在RN上积分,可得 显然,这与(7)式矛盾,所以(u′,0)不是方程组(1)的解.同理验证(0,v′)也不是方程组(1)解,所以(u′, v′)是方程组(1)的一正解.证毕. 参考文献: [1] Binding P A,Drabek P,Huang Y X.Existence of multiple solutions of critical quasilinear ellip tic Neumann p roblems [J].Nonl Anal,TMA 2000,42(4):613-629. [2] Guo ZM.Some existence and multiplicity results fo r a class of quasilinear ellip tic eigenvalue p roblem s[J].Nonl Anal, TMA,1992,18(10):957-971. [3] D rábek P,Pohozaev S I.Positive solutions fo r the p-Laplacian:app lication of the fiberingmethod[J].Proceedingsof the Royal Society of Edinburgh,1997,127(A):703-726. [4] Clément P,Fleckinger J,M itidieri E,et al.Existenceof positive solutions fo r quasilinear ellip tic systems[J].JDifferential Equations,2000,166(2):455-477. [5] 乔瑞霞,崔国忠.一类退化反应扩散方程组解的整体存在性与有限爆破问题[J].郑州大学学报:理学版,2006,38(4): 7-11. [6] Huang X Y.A note on asymp to tic behavio r of positive solution fo r some ellip tic equations[J].Nonl Anal Theo ry M ethods Appl,1997,29(5):533-537. [7] Gilbarg D,Trudinger N S.Ellip tic Partial Differential Equationsof Second Order[M].Berlin:Sp ringer,1998. [8] Binding P A,D rabek P,Huang Y X.On Neumann boundary value p roblem s for some quasilinear ellip tic equations[J]. Electron JDifferential Equations,1997,1997(5):1-11. Existence of Positive Solution for Quasilinear Systems via Mountain Pass Lemma Q IRui-gai, YANG Guo-ying A p-Lap lacian system w ith Dirichlet boundary conditions is investigated.By using the mountain pass lemma and the p roperty of integral,the result of the existence of positive solutions w ith suitable parameters is obtained. p-Lap lacian system;mountain pass lemma;critical point O 175.25 A 1671-6841(2010)03-0019-04 2009-06-21 河南省自然科学基金资助项目,编号082300410310;河南理工大学博士基金资助项目,编号B2008-56;河南理工大学研究生学位论文创新基金资助项目,编号2008-M-29. 祁瑞改(1983-),女,硕士研究生,主要从事椭圆型方程组正解的存在性研究,E-mail:qiruigai@163.com.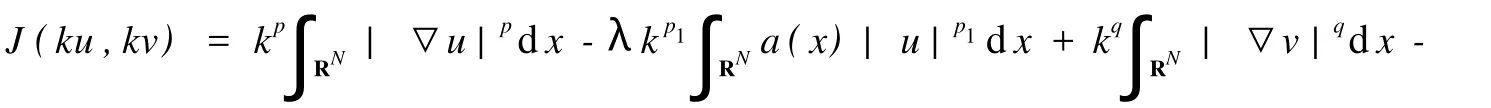
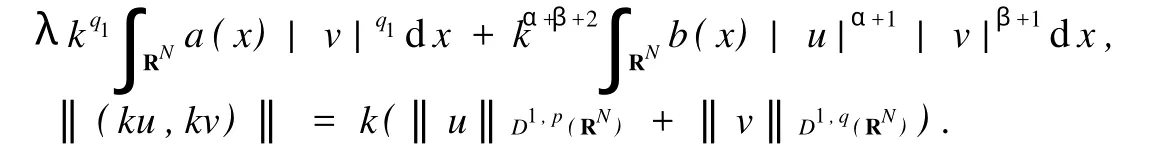
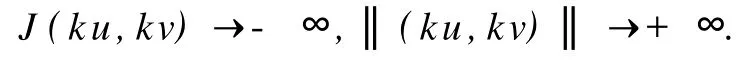
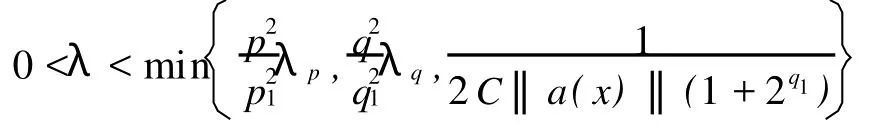
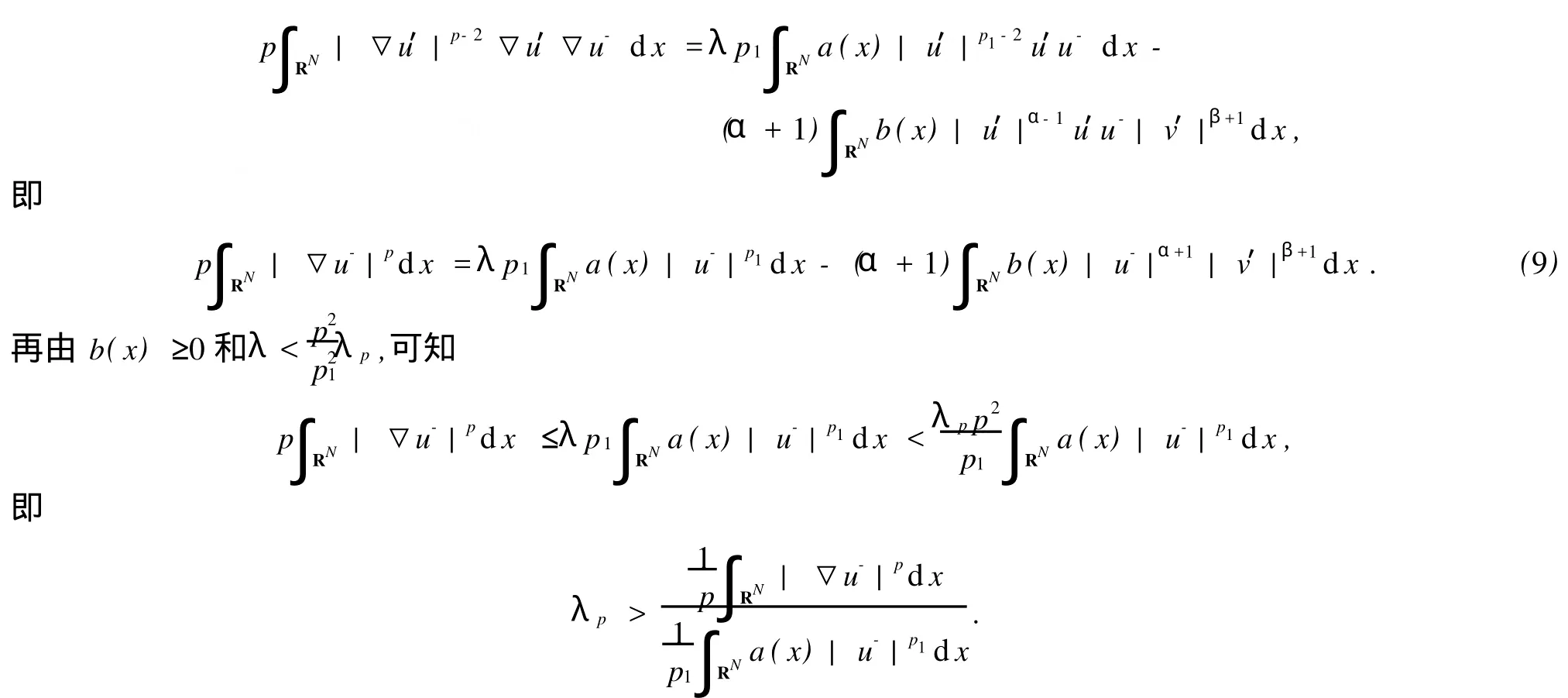
(Department of M athem atics,Henan Poly technic University,Jiaozuo 454000,China)
