数学物理方法在半导体PN结分析中的应用

张怀广

(濮阳职业技术学院,河南濮阳 457000)

数学物理方法在半导体PN结分析中的应用

张怀广

(濮阳职业技术学院,河南濮阳 457000)

半导体PN结具有的单向导电性,是制造半导体器件的基础,使电子信息技术得以高速发展.我们用数学思想方法分析和解释半导体PN结中电流的运动规律,探讨了一个新的分析方法和教学思路.

数学物理方法;半导体 PN结;载流子扩散电流;电荷的连续方程

1 前言

数学物理方法:将数学思想方法应用于现代高科技各专业技术领域,并构建成典型的(物理)模型和解决问题的方法,从而形成科学研究中实用性很强的数学物理方法.

半导体PN结的模型:在纯净的硅晶体内掺入特定杂质形成杂质半导体,例如掺入杂质磷元素形成电子型半导体,掺入杂质硼元素形成空穴型半导体.在电子型半导体和空穴型半导体的交界面附近由于电子和空穴的扩散运动而相遇中和,不能移动的杂质离子形成的空间电荷区,成为半导体PN结.半导体 PN结阻止电子和空穴的进一步扩散运动,达到平衡状态.半导体PN结具有的单向导电性使电子信息技术得以高速发展.我们用数学思想方法分析和解释半导体PN结中电流的运动规律.探讨了一个新的分析方法和教学思路.

2 电子载流子的扩散过程

我们知道,在载流子浓度处于均匀的半导体材料中,不加外电场时,不会产生电流.我们称其为平衡态载流子.如果在半导体中,某处的载流子浓度大于平衡载流子浓度(也称为不均匀)时,载流子会由浓度大的地方向浓度小的地方扩散,这样就在半导体中形成了扩散电流.

仔细观察如图1(a)所示的本征半导体,在其左端用光照射,在光的激发下,由于光电效应使半导体左端增加了新的载流子浓度(电子或空穴),从而引起了半导体内部载流子的浓度分布不均匀.以电子运动为例且只考虑一维的扩散运动,可以观察到电子载流子浓度由大到小的分布如图1(b)所示.

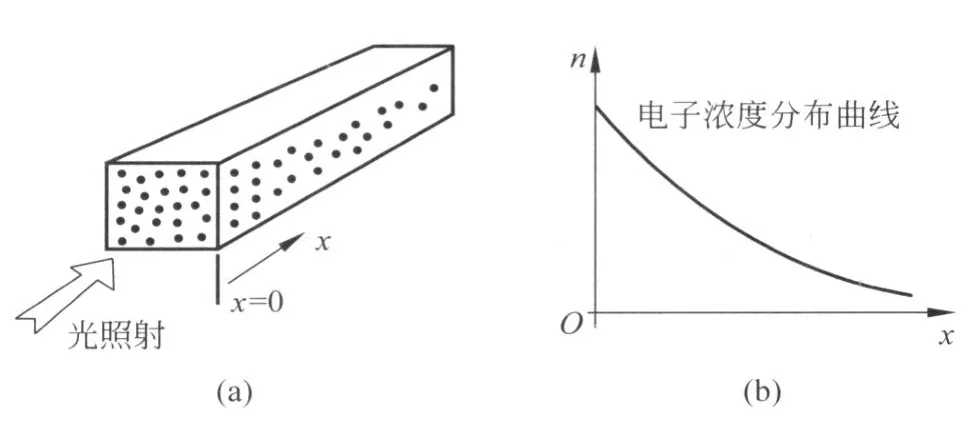
图 1

可以发现:虽然没有外电场,仅由电子载流子浓度的差异就可以引起电荷的流动,由此形成扩散电流.因此可以根据电子浓度分布曲线的斜率,找出由电子载流子扩散引起的扩散电流 In的估算公式

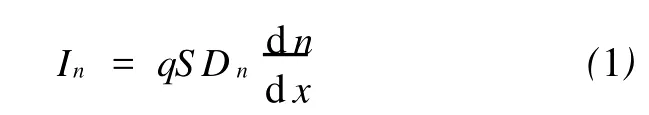
依此类推,也可以找出由空穴载流子扩散引起的扩散电流 Ip的估算公式

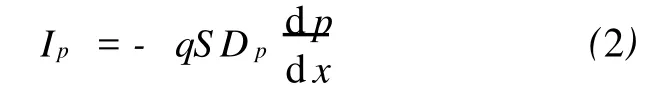
式中:In——沿 x轴方向由电子载流子引起的扩散电流;Ip——沿 x轴方向由空穴载流子引起的扩散电流;S——半导体材料的截面积;q——电荷量;n——电子浓度;p——空穴浓度;Dn——电子扩散系数,一般硅材料的电子扩散系数 Dn=33cm2/s;Dp——空穴扩散系数,一般硅材料的空穴扩散系数Dp=13cm2/s.

3 电荷的连续方程

在上述用光照射半导体材料的左端所产生非平衡载流子的现象中,可知它们的浓度与距离 x有关,越靠近光照射的地方浓度越大;当光照停止后,非平衡载流子的运动将逐渐消失,浓度逐渐趋于平衡,所以非平衡载流子的浓度也与时间有关.连续方程就是考虑到上述两个因素,用来描述载流子变化规律的数学表达式.

我们在图1半导体材料中截出一块小体积如图2所示.为方便起见,用空穴载流子来描述非平衡载流子.

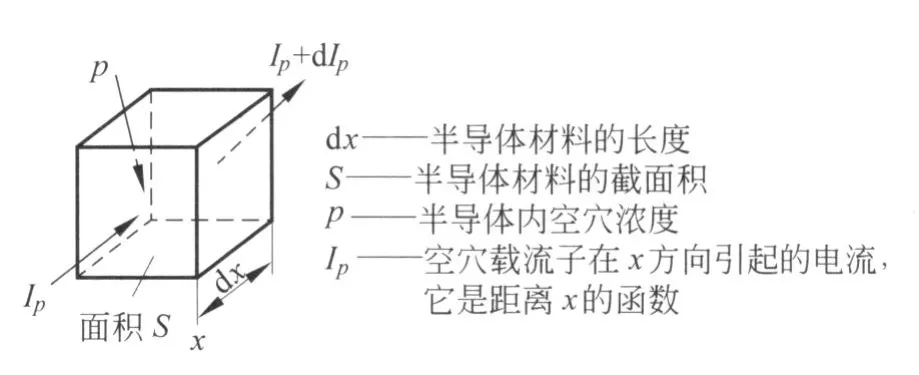
图 2

设在同一时间 t内,流入小体积 x处的电流是Ip,流出小体积 x+d x处的电流是Ip+d Ip,假若d Ip>0,则每秒内流出小体积的电荷量将大于流入的电荷量.因此,每秒小体积内电荷量的减少值是d Ip.而空穴的电荷量为q,于是每秒小体积S d x内空穴数的减少量是

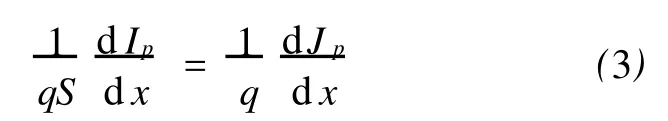
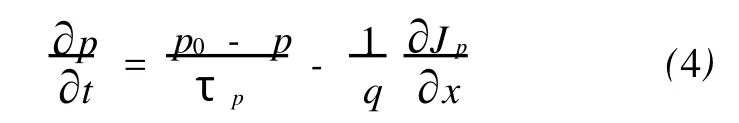
这就是电荷的连续方程,它将非平衡载流子的浓度 p与距离 x和时间t组合在一个数学关系式中,反映了半导体材料中电荷量的守恒关系.

4 电荷的连续方程应用于PN结的分析

我们还可以将电荷的连续方程应用于PN结的分析.当给PN结两端加上一个稳定的直流电压V时,N区靠近结边界附近的空穴浓度 p只是距离x的函数,而与时间 t无关.因此式(4)中的,再将式(2)代入式(4),整理得

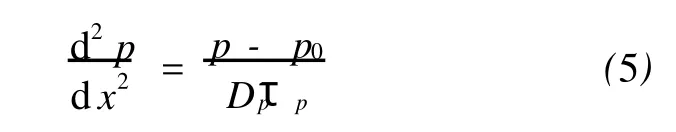
若用 p′表示某一时间非平衡的空穴浓度,即:p′=p-p0,而平衡值 p0与时间 t、距离 x无关,我们可以令:Lp=Dpτp(Lp为扩散长度),那么式(5)可以改写为下面的形式

这个二阶微分方程的解为

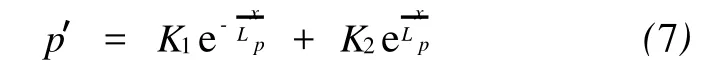
观察这个微分方程的解时可以发现:半导体材料沿 x方向距离的长度比扩散长度Lp大得多,故式(7)第二项将变得非常大,这实际上是不可能的,因此第二个积分常数 K2=0.再令 x=0,可以求出第一个积分常数 K1=p′(0).最后可以得出N区靠近PN结边界附近的非平衡空穴浓度 p与距离x的关系式.

由此得出结论:在PN结边界附近,非平衡空穴浓度 p的分布是按指数规律衰减的,而且空穴在扩散中,不但浓度逐渐减小,其斜率(浓度梯度)也不断减小.

5 结束语

利用数学物理方法,我们在对电子载流子扩散过程的分析过程中导出了电荷的连续方程,得出非平衡载流子的浓度 n或p与距离x和时间t的数学关系式.我们利用这个关系式不仅可以解释PN结两端半导体材料中空穴或电子浓度的分布规律,还为后续课程内容中解释PN结中多数载流子复合电流的变化规律提供了新的数学工具.

[1] 童诗白.模拟电子技术基础[M].北京:人民教育出版社,1980

[2] 严镇军.数学物理方程[M].合肥:中国科学技术大学出版社

APPL ICATIONOFMATH-PHYSICAL M ETHOD IN THE ANALYSISOF SEM ICONDUCTOR PN JUNCTION

Zhang Huaiguang
(Puyang Vocational and Technical College,Puyang,Henan 457000)

The unilateral conduction of semiconductor PN junction is the base of semiconductor devicesmanufacturing.It contributes to the rapid development of electronics and info rmation technology.In this paper,we analyze and exp lain themotion law of current in semiconductor PN junction by mathematical thinking method.New analysis method and teaching idea have been discussed.

math-physical method;semiconductor PN junction;diffusion current of carrier;continuous equation of charge

2008-09-22)

张怀广,研究生毕业,副教授.