弹簧摆的内共振特性分析
2010-09-06郑建龙虞献文浙江师范大学数理与信息工程学院浙江金华321004
郑建龙 虞献文(浙江师范大学数理与信息工程学院,浙江金华 321004)
弹簧摆的内共振特性分析
郑建龙 虞献文(浙江师范大学数理与信息工程学院,浙江金华 321004)
首先提出了一种弹簧摆模型,通过谐波平衡法对弹簧摆的内共振现象进行了解析处理,得到了弹簧摆内共振条件以及X、Z两模态能量之间的转换关系.再利用数值模拟得到弹簧摆内共振时的时序图、相图、轨迹图、能量图以及内共振耦合区域图等,分析表明,解析和数值模拟的结果与实验结果吻合一致.
弹簧摆;非线性振动;内共振;谐波平衡法
弹簧摆的运动情形与恢复力带平方非线性系统相关[1],是工程中较典型的非线性运动之一.它与电子回旋加速器的振动、船舶的运动、旋转轴的运动等有联系.在铅直平面内运动的弹簧摆可看成两个自由度的振动系统,有两个固有频率,当满足内共振条件时,两个振动模态强烈地耦合,发生一种振动激发另一种振动的内共振现象.在不计阻力的条件下,系统的能量在两种振动模态之间不断地变换而不衰减,振幅和相位周期性变化.关于弹簧摆的动力学行为在数值分析和实验等方面分别已有一些研究[2~6],但在理论方面讨论很少,在数值分析方面也没有作详细讨论.本文从系统的势能出发,根据拉格朗日公式推得弹簧摆的耦合振动方程,再采用谐波平衡法得出弹簧摆内共振条件和两模态能量之间的转换关系,最后利用数值模拟得到弹簧摆内共振时的振动位移图、相图、轨迹图、能量图以及内共振区域图等,并通过位移图、相图、轨迹图和能量图等比较全面地分析弹簧摆内共振的特点,得出了与文献[3]相同的结果.
1 弹簧摆系统内共振的理论分析
1.1 弹簧摆系统的振动模型
在弹簧下面挂一小球,小球的质量为m,可看成质点,弹簧的质量相对于小球可忽略不计,便组成了一个弹簧摆系统.图1为弹簧摆示意图及相关坐标的定义.O点为摆球的平衡位置.

图1 弹簧摆示意图及相关坐标的定义
弹簧摆系统的势能为

其中,k为弹簧的劲度系数;m为摆球的质量;l0为弹簧的原长,根据拉格朗日公式[7],由式(1)至式(3)得系统的动力学方程为


1.2 弹簧摆系统的内共振条件
为了利用谐波平衡法[8~10]推出弹簧摆系统的内共振条件,先令(6)和(7)两式右边分别等于零,系统的 x和z两个振动分别是角频率为ωp、ωs的简谐振动,运动方程为
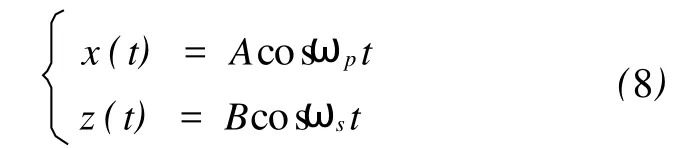
再将简谐振动形式式(8)代入式(6),得
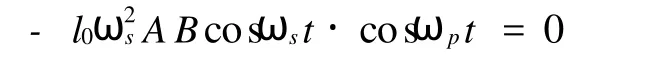
化简后得

从式(9)可知,式(6)右边可展开为角频率分别为ωs+ωp和ωs-ωp两个驱动力的线性叠加,其中前者远离共振条件,可忽略不计.当后者的角频率ωs-ωp与x振动模态的角频率ωp相等时,产生共振现象,即

同理,将简谐振动形式式(8)代入式(7),得

化简后得

从式(11)又可知,当 x2的角频率与 z振动模态的角频率相等时产生共振现象,即 x方向的振动会激发z方向的振动,同样可得到式(10).这样,系统的两个模态强烈耦合,出现内共振现象.因此式(10)为弹簧摆内共振条件.
1.3 弹簧摆系统内共振两模态之间的能量关系
由于(6)和(7)两式右边的驱动力较弱,因此,两个振动的振幅和相位变化可视为随时间的慢变量.这样,在考虑弹簧摆内共振条件下,可将(6)和(7)两式的解分别写成如下形式

再将(12)和(13)两式分别代入(6)和(7)两式,根据谐波平衡法,利用两方程两边的 sin(ωpt+φ),cos(ωpt+φ),sin(2ωpt+ψ)和cos(2ωpt+ψ)项的系数相等,可得关于 A,B,φ,和ψ的微分方程组其中,M0为与系统初始能量成正比的常量.式(18)为弹簧摆系统内共振两模态之间的能量关系,说明弹簧的伸缩和摆动均有界,而且两种运动的幅值交替增减,能量不断在两种振动形式之间转换.
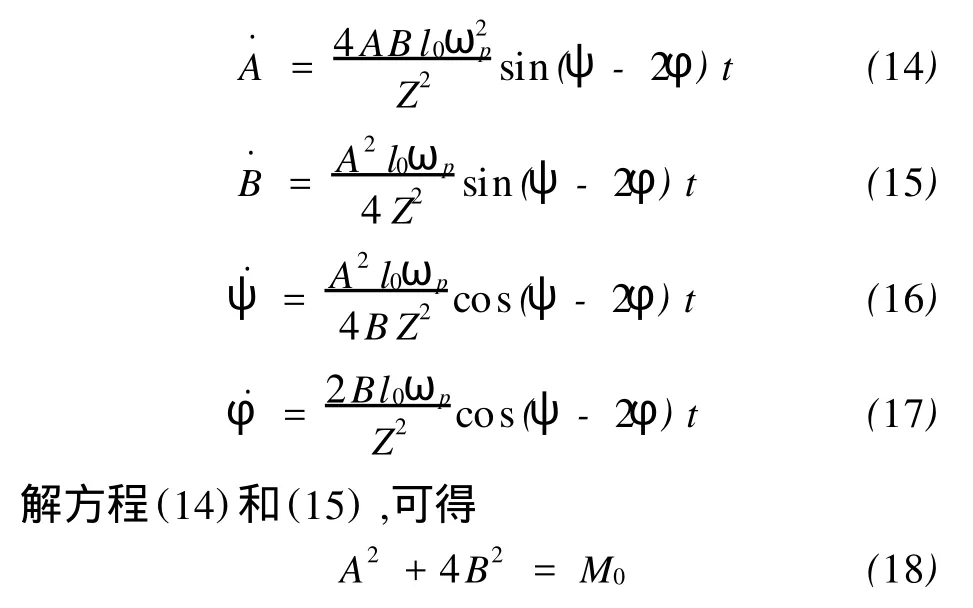
2 弹簧摆系统内共振特性的数值模拟
为了数值求解弹簧摆的非线性动力学系统式(6) 和式 (7),先引入变量 y1=x,y2=x·,y3=z,y4=z·,再代入系统式(6)和式(7)并进行降阶处理,得到

其中,y1,y2,y3,y4是系统动力学参量;ωp,ωs,l0,Z是系统参数 ;表示对 t的导数.
利用高阶 Runge-Kutta方法[11]求解降阶的非线性动力学系统式(19)得出数值解,从而研究弹簧摆系统内共振特性.为了检验解析和数值模拟结果的正确性,我们选取文献[3]中的实验数据m=0.048kg,k=2.31N/m,z0=0.82m,g=9.81N/m2作为研究参数,由这些参数可得系统参数ωp=3.46rad/s,ωs=6.89rad/s,满足内共振条件.再选取两种不同的摆球初始条件 x0=0.141m,z0=0.109m与x0=0.141m,z0=0.051m来考察弹簧摆位移、相图、轨迹和能量的关系,并给出了弹簧摆系统内共振耦合发生的区域.
由图2可知,无论是弹簧摆作小角度摆动(如图2(a)所示),还是作大角度摆动(如图2(b)所示)都有倍频关系的内共振现象,这与上述理论讨论结果式(10)一致.但唯有作小角度摆动,才有系统的两个模态强烈耦合的情形.该结果与文献[3]中的实验结果相吻合.这也说明存在弹簧摆系统的两个模态耦合的临界状态.从图3可以看出,根据相平面理论,弹簧摆作大小角度摆动的内共振解都是稳定的.而从图4又可知,弹簧摆作大小角度摆动的伸缩和摆动均有界.这与文献[3]中的实验结果一致.
图5中的左图和中图分别为在初始条件x0=0.141m,z0=0.109m下 X、Z两模态内共振的能量随时间的变化曲线,右图为弹簧摆系统内共振总能量.从能量图上可以看出,弹簧摆系统内共振时,能量在两模态间转换,并且保持总能量不变.这与上述理论讨论结果式(18)一致.


最后通过大量的数值模拟,我们得出了弹簧摆系统内共振耦合发生的区域图,如图6所示,这为讨论与恢复力带平方非线性系统的内共振耦合现象的实验研究提供了一定的理论依据.
3 结论
本文通过建立一种弹簧摆系统模型,分别用解析和数值模拟的方法分析了弹簧摆系统的内共振现象.结果表明,应用谐波平衡法解析处理弹簧摆系统的非线性内共振问题有效.不仅解释了实验结果,而且还得到了数值模拟的证实.这将为讨论诸如电子回旋加速器的振动、船舶的运动、旋转轴的运动等与恢复力带平方非线性系统有联系的内共振问题提供参考.
[1] 褚亦清,李翠英.非线性振动分析[M].北京:北京理工大学出版社,1996.975~983
[2] 石玉仁,薛具奎.弹簧摆的混沌行为[J].西北师范大学学报,2001:37(3):91~97
[3] 司丽荣,张竞夫.弹簧摆内共振现象的实验研究[J].物理实验,2002,22(3):9~12
[4] 王建平,刘宏昭,原大宁,苏致霄.一类非线性振动系统改进状态空间模型及其数值方法[J].应用力学学报,2002,19(4):112~116
[5] Cuerno R,Ranada A F,Ruiz-Lorenzo J J.Deter-ministic chaos in the elastic pendulum:A simple laboratory for nonlinear dynamics[J].Am.J.Phys,1992,60(1):73
[6] Davidovic D M,Anicin B A,Babovic V M.The libration lim its of the elastic pendulum[J].Am.J.Phys,1996,64(3):338
[7] 王永岩.理论力学[M].北京:科学出版社,2007.428~438
[8] 陈树辉.强非线性振动系统的定量分析方法[M].北京:科学出版社,2007.169~174
[9] 刘延柱,陈立群.非线性振动[M].北京:高等教育出版社,2001.57~59
[10] 朱因远,周纪卿.非线性振动和运动稳定性[M].西安:西安交通大学出版社,1992.32~36
[11] Press W H,Teukolsky S A,Vetterling W T.Numerical Recipes-The A rt of Scientific Computing[M].Cambridge,U K:Cambridge University Press,1996
ANALYSISOF THE AUTOPARAM ETRIC RESONANCE OF A SPRING PENDULUM
Zheng Jianlong Yu Xianwen
(College of Mathematics,Physics and Information Engineering,Zhejiang Normal University,Jinhua,Zhejiang 321004)
In this paper,w e have put fo rward a sort of sp ring pendulum model.Through the harmonic balance method,the autoparametric resonance of the sp ring pendulum has been analytically p rocessed.The condition of the autoparametric resonance of the sp ring pendulum has been obtained,and the transform relationship between X and Z models has been discussed. Moreover, the graphs of disp lacement,phase, trajectory,energy and autoparametric resonance area have been numerically obtained.Analyses indicate that the results obtained here agree w ell w ith the experimental results.
sp ring pendulum;nonlinear vibration;autoparametric resonance;harmonic balance method
2009-04-16;
2009-09-21)
浙江省科技计划项目(2008C31013);金华市科技项目(2006-1-017).
