旅客留剩率与列车上座率的关系研究
2010-09-06左大杰王慈光倪少权
左大杰,王慈光,倪少权
(西南交通大学 交通运输学院,四川 成都 610031)
1 研究背景
由于我国特有的文化传统和经济发展,在节假日经常形成客流数量巨大,而且在方向、结构、时间和地区分布上不均衡的超强客流[1]或高峰客流[2]。如何面对每年节假日的旅客运输,特别是春节、“十一”等长假期的旅客运输,是我国铁路部门应认真研究的问题。正确预测节假日客流量,是编制节假日旅客运输计划、加开临时旅客列车、组织均衡运输等项工作的基础[3]。
由于节假日客流在方向、时间和空间上不均衡,若列车开行数量足够多,则旅客不会有留剩,但列车上座率和车底运用效率会降低,不利于提高企业经济效益;反之,列车上座率会较高,但是将出现旅客有留剩的情况,服务水平降低。由此可见,旅客留剩率和列车上座率是反映服务水平和经济效益的重要指标,探讨确定性与不确定性客流条件下两者的关系,可以为合理制定列车开行方案提供理论依据。
2 确定性客流条件下的旅客留剩率和列车上座率
2.1 基本原理
设铁路某确定性 OD 客流量为 X,拟开行 n 列定员为 Y 人的列车输送该 OD 客流量。设旅客留剩率为βL,一般情况下,βL越小越好。在决策者给出预期值βLmax后,则有:

同理,设列车上座率为βS,在其他条件一定的情况下,βS越大越好。设决策者给出预期值 βSmin后,则有:

由公式⑴和公式⑵可知,在客流和列车定员已知的情况下,较小的列车开行数量对应的旅客留剩率和列车上座率均较高;反之,较大的列车开行数量对应的旅客留剩率和列车上座率均较低。因此,在确定性客流条件下,较低的旅客留剩率和较高的列车上座率是相互对立的。
2.2 数量关系
若预期较低的旅客留剩率(即βLmax较小)和较高的列车上座率(即βSmin较大)通常会导致列车开行方案不可行。一般地,联立公式⑴和公式⑵:当[X(1-βLmax)/Y,X/(Y×βSmin)]内有整数时,n=整数解;其他时,n无解。
在有解的条件下,给定旅客留剩率目标 βLmax,解得临界条件下的列车上座率为:

2.3 算例分析
(1)已知铁路某 OD 客流量为2250人次/d,列车定员为670人,则由公式⑴和公式⑵可得:若开行3列列车,则列车上座率 βS=111.9%,旅客留剩率βL=10.7%;若开行4列列车,则列车上座率 βS=84.0%,旅客留剩率 βL=-9.1%(负号表示列车能力有富余)。若决策者提出“旅客留剩率不大于10%,列车上座率不小于85%”的目标,则其在理论上是不可实现的。
(2)已知铁路某 OD 客流量为2.25万人次/d,列车定员为670人,则由公式⑴和公式⑵可得:若开行33列列车,则列车上座率 βS=101.8%,旅客留剩率 βL=1.7%;若开行34列列车,则列车上座率βS=98.8%,旅客留剩率 βL=-1.2%。若决策者提出“旅客留剩率不大于10%,列车上座率不小于85%”的目标,则显然是可以实现的。
算例表明,大客流对同时降低旅客留剩率和提高列车上座率是有利的。
3 不确定客流条件下的旅客留剩率和列车上座率
3.1 基本原理
根据对某客流连续3年的观测,经过对其进行时间序列分析,发现客流以年度、周(或黄金周)为周期表现出年度周期性和星期周期性;在一个周期内表现出波动性,即一个周期由若干个波段组成;在一个波段内表现为随机性,即客流量一般服从某一特定的随机分布。根据概率论的相关理论,仅研究一个波段内的随机性客流条件下旅客留剩率和列车上座率的关系。
设铁路某客流 OD 服从正态分布X~N(μ,σ2),拟开行 n 列定员为 Y 人的列车输送该 OD客流量。显然,前述公式不能描述随机客流条件下的旅客留剩率等指标。设 αL为旅客留剩率不大于 βLmax的概率,则有:
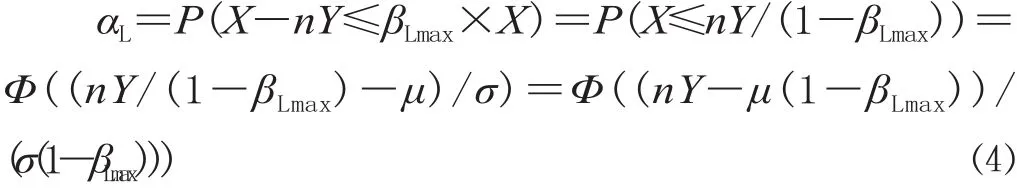
通常情况下,决策者期望出现旅客留剩率不大于某水平的概率不小于给定水平(设为αLmin),则有:
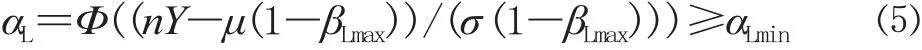
同理,设αS、αX分别表示列车上座率不小于βSmin、列车虚糜率不大于βXmax的概率,决策者期望以上概率分别不小于给定水平αSmin、αXmin,则有:
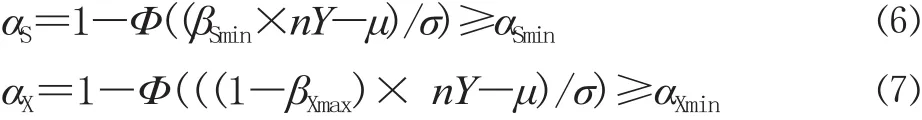
其中,Φ(X)为标准正态分布函数。显然,若βSmin+βXmax=1,则αS=αX。因此,列车上座率与列车虚糜率也仅需考虑其中一个即可。
由公式⑸和公式⑹可知,在客流和列车定员已知的情况下,列车开行数量越小,列车上座率大于给定水平的概率就越大,而旅客留剩率小于给定水平的概率也就越小;反之,列车开行数量越大,旅客留剩率小于给定水平的概率就越大,而列车上座率大于给定水平的概率就越小。由此可见,在随机性客流条件下,同时追求较低的旅客留剩率和较高的列车上座率是相互对立的。
3.2 数量关系
联立公式⑸和公式⑹:当[(μ(1-βLmax)+σ(1-βLmax)×Φ-1(αLmin))/Y,(μ+σΦ-1(1-αSmin))/(Y×βSmin)]内有整数时,n=整数解;其他时,n 无解。
在有解的条件下,给定旅客留剩率目标 βLmax及其满足的概率 αLmin,联立公式⑸和公式⑹解得临界条件下的列车上座率不小于给定目标 βSmin的概率 αS为:
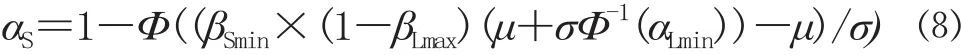
3.3 算例分析
已知某客流服从正态分布X~N(μ,σ2),列车定员Y=670。
(1)在 μ=2250,σ=225时,旅客留剩率不大于 βLmax的概率 αL如图1所示,列车上座率不小于βSmin的概率 αS如图2所示。由图1、图2可知,αL与 αS是一组对立的指标,如果使旅客留剩率不超过给定水平的概率越高,则需要开行数量更多的列车,这给列车上座率的提高带来较大困难。例如,①若欲使旅客留剩率不大于0(即为0)的概率不小于100%(即为100%),则理论上必须开行5列列车,而此时列车上座率不小于给定水平100%、95%、90%、85%、80%、75%的概率分别为0.0000、0.0000、0.0003、0.0040、0.0280、0.1217;②若欲使旅客留剩率不大于0(即为0)的概率不小于97%,则理论上必须开行4列列车,而此时列车上座率不小于给定水平100%、95%、90%、85%、80%、75% 的概率分别为0.0280、0.0942、0.2358、0.4505、0.6812、0.8569。
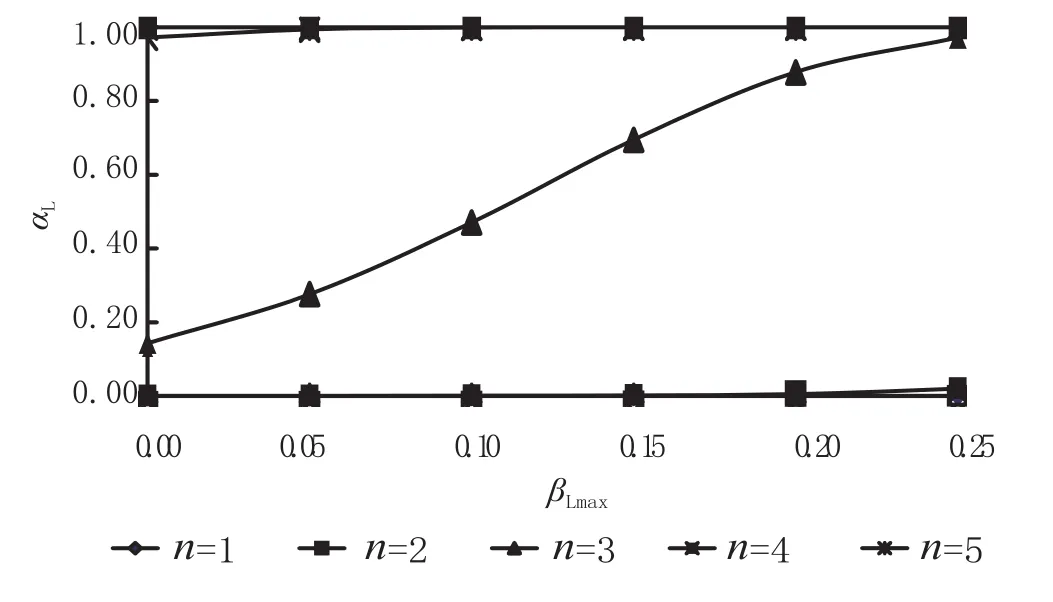
图1 旅客留剩率不大于 βL 的概率αL(μ=2250,σ=225)
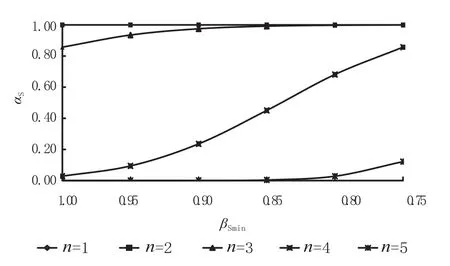
图2 列车上座率不小于βS的概率αS(μ=2250,σ =225)
(2)在 μ=22500,σ=2250时,旅客留剩率不大于 βLmax的概率 αL如图3所示,列车上座率不小于 βSmin的概率 αS如图4所示。由图3、图4可知,相对于小客流,大客流虽然 αL与 αS仍然对立,但是开行数量增减1列对旅客留剩率和列车上座率的影响均不太大。
当客流量均值相对列车定员很大时,αL与 αS对列车开行数量的弹性较小,而当客流量均值相对列车定员较小时,αL与αS对列车开行数量的弹性很大。
(3)在 μ=22500,σ=2250时,给定旅客留剩率预期值 βLmax及其满足概率 αL,由公式⑻可求得不同旅客上座率预期值 βSmin及其概率 αS之间的关系,如图5所示。由此可知,在βLmax、αL给定条件下 βSmin与αS负相关,对βLmax、αL的追求越高,βSmin满足概率 αS就越低,且两者的负相关关系越明显。这说明预期的旅客留剩率不大于某一较小值的概率越大,其与列车上座率的矛盾就越突出。
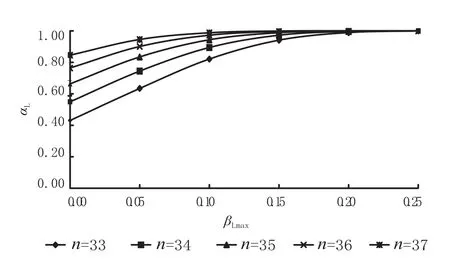
图3 旅客留剩率不大于 βL 的概率 αL(μ=22500,σ=2250)
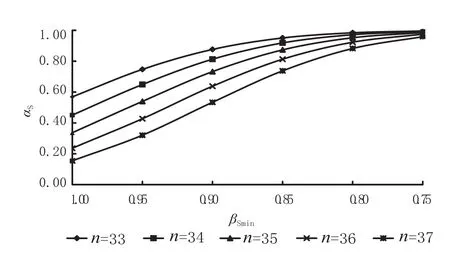
图4 旅客留剩率不小于 βS 的概率 αS(μ=22500,σ=2250)
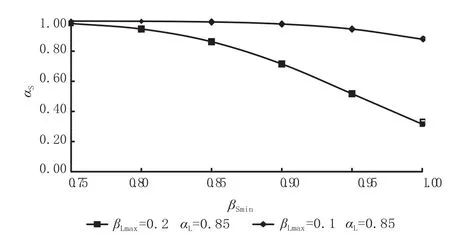
图5 固定 βLmax、αL 条件下 βSmin 与 αS 的关系曲线
4 结束语
(1)对于确定性客流,在客流和列车定员已知的情况下,较小的列车开行数量对应较高的旅客留剩率和较高的列车上座率;反之,较大的列车开行数量对应较低的旅客留剩率和较低的列车上座率。
(2)对于随机性客流,在客流和列车定员已知的情况下,列车开行数量越小,列车上座率大于给定水平的概率越大,而此时旅客留剩率小于给定水平的概率越小;反之,列车开行数量越大,旅客留剩率小于给定水平的概率越大,而列车上座率大于给定水平的概率越小。
(3)无论确定性客流还是不确定客流,旅客留剩率和列车上座率是一对相互对立的指标。一个指标的改善必然以牺牲另一指标为代价。制定列车开行方案应综合考虑运营成本和服务水平。
(4)大客流对于列车上座率和旅客留剩率的弹性较小,建议组织若干支小客流在位于路网中的某些重要大站采用换乘集结的方式形成大客流后输送,以便合理兼顾车底的运用效率和旅客服务水平 。
:
[1]薛成海,周 强. 超强客流条件下铁路客运营销及运输组织有关问题探讨[J]. 石家庄铁道学院学报,2001,14(2):65-68.
[2]王 华,周亚丽,李雪婷. 客流高峰期铁路运输组织的思考[J]. 铁道运输与经济,2005,27(1):52-54.
[3]孙天沛. 铁路节假日旅客流量的预测[J]. 铁道运输与经济,1982,4(1):32-40.
